Detecting Near-Duplicates for Web Crawling － simhash与重复信息识别

随着信息爆炸时代的来临，互联网上充斥着着大量的近重复信息，有效地识别它们是一个很有意义的课题。例如，对于搜索引擎的爬虫系统来说，收录重复的网页是毫无意义的，只会造成存储和计算资源的浪费；同时，展示重复的信息对于用户来说也并不是最好的体验。造成网页近重复的可能原因主要包括： 

• 镜像网站
• 内容复制
• 嵌入广告
• 计数改变
• 少量修改

一个简化的爬虫系统架构如下图所示： 




事实上，传统比较两个文本相似性的方法，大多是将文本分词之后，转化为特征向量距离的度量，比如常见的欧氏距离、海明距离或者余弦角度等等。两两比较固然能很好地适应，但这种方法的一个最大的缺点就是，无法将其扩展到海量数据。例如，试想像Google那种收录了数以几十亿互联网信息的大型搜索引擎，每天都会通过爬虫的方式为自己的索引库新增的数百万网页，如果待收录每一条数据都去和网页库里面的每条记录算一下余弦角度，其计算量是相当恐怖的。 

我们考虑采用为每一个web文档通过hash的方式生成一个指纹（fingerprint）。传统的加密式hash，比如md5，其设计的目的是为了让整个分布尽可能地均匀，输入内容哪怕只有轻微变化，hash就会发生很大地变化。我们理想当中的哈希函数，需要对几乎相同的输入内容，产生相同或者相近的hashcode，换句话说，hashcode的相似程度要能直接反映输入内容的相似程度。很明显，前面所说的md5等传统hash无法满足我们的需求。 

simhash是locality sensitive hash（局部敏感哈希）的一种，最早由Moses Charikar在《similarity estimation techniques from rounding algorithms》一文中提出。Google就是基于此算法实现网页文件查重的。我们假设有以下三段文本： 

• the cat sat on the mat
• the cat sat on a mat
• we all scream for ice cream

使用传统hash可能会产生如下的结果： 

引用

irb(main):006:0> p1 = 'the cat sat on the mat' 
irb(main):005:0> p2 = 'the cat sat on a mat' 
irb(main):007:0> p3 = 'we all scream for ice cream' 
irb(main):007:0> p1.hash 
=> 415542861 
irb(main):007:0> p2.hash 
=> 668720516 
irb(main):007:0> p3.hash 
=> 767429688

使用simhash会应该产生类似如下的结果： 

引用

irb(main):003:0> p1.simhash 
=> 851459198 
00110010110000000011110001111110 

irb(main):004:0> p2.simhash 
=> 847263864 
00110010100000000011100001111000 

irb(main):002:0> p3.simhash 
=> 984968088 
00111010101101010110101110011000

海明距离的定义，为两个二进制串中不同位的数量。上述三个文本的simhash结果，其两两之间的海明距离为(p1,p2)=4，(p1,p3)=16以及(p2,p3)=12。事实上，这正好符合文本之间的相似度，p1和p2间的相似度要远大于与p3的。 

如何实现这种hash算法呢？以上述三个文本为例，整个过程可以分为以下六步： 
1、选择simhash的位数，请综合考虑存储成本以及数据集的大小，比如说32位 
2、将simhash的各位初始化为0 
3、提取原始文本中的特征，一般采用各种分词的方式。比如对于"the cat sat on the mat"，采用两两分词的方式得到如下结果：{"th", "he", "e ", " c", "ca", "at", "t ", " s", "sa", " o", "on", "n ", " t", " m", "ma"} 
4、使用传统的32位hash函数计算各个word的hashcode，比如："th".hash = -502157718 
，"he".hash = -369049682，…… 
5、对各word的hashcode的每一位，如果该位为1，则simhash相应位的值加1；否则减1 
6、对最后得到的32位的simhash，如果该位大于1，则设为1；否则设为0 

整个过程可以参考下图： 



按照Charikar在论文中阐述的，64位simhash，海明距离在3以内的文本都可以认为是近重复文本。当然，具体数值需要结合具体业务以及经验值来确定。 
  
使用上述方法产生的simhash可以用来比较两个文本之间的相似度。问题是，如何将其扩展到海量数据的近重复检测中去呢？譬如说对于64位的待查询文本的simhash code来说，如何在海量的样本库（>1M）中查询与其海明距离在3以内的记录呢？下面在引入simhash的索引结构之前，先提供两种常规的思路。第一种是方案是查找待查询文本的64位simhash code的所有3位以内变化的组合，大约需要四万多次的查询，参考下图： 



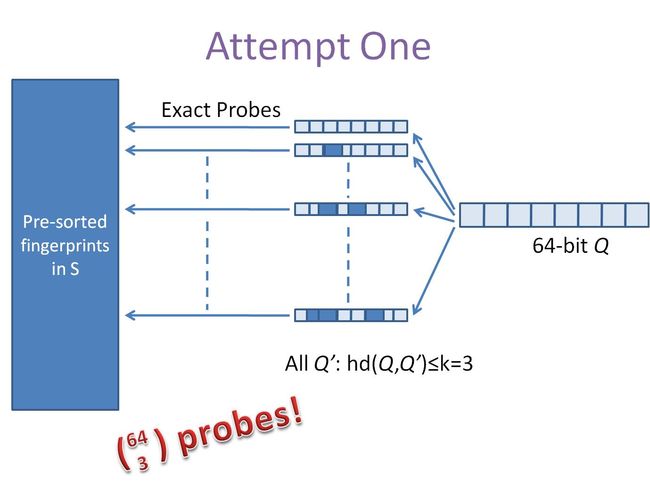
另一种方案是预生成库中所有样本simhash code的3位变化以内的组合，大约需要占据4万多倍的原始空间，参考下图： 



显然，上述两种方法，或者时间复杂度，或者空间复杂度，其一无法满足实际的需求。我们需要一种方法，其时间复杂度优于前者，空间复杂度优于后者。 

假设我们要寻找海明距离3以内的数值，根据抽屉原理，只要我们将整个64位的二进制串划分为4块，无论如何，匹配的两个simhash code之间至少有一块区域是完全相同的，如下图所示： 



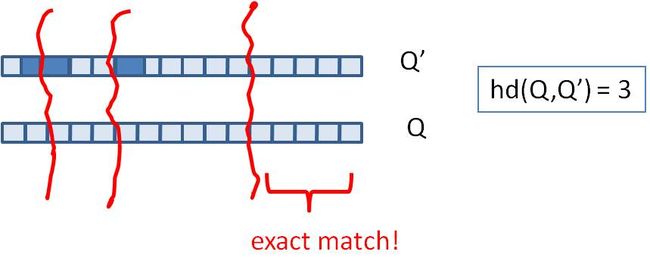
由于我们无法事先得知完全相同的是哪一块区域，因此我们必须采用存储多份table的方式。在本例的情况下，我们需要存储4份table，并将64位的simhash code等分成4份；对于每一个输入的code，我们通过精确匹配的方式，查找前16位相同的记录作为候选记录，如下图所示： 



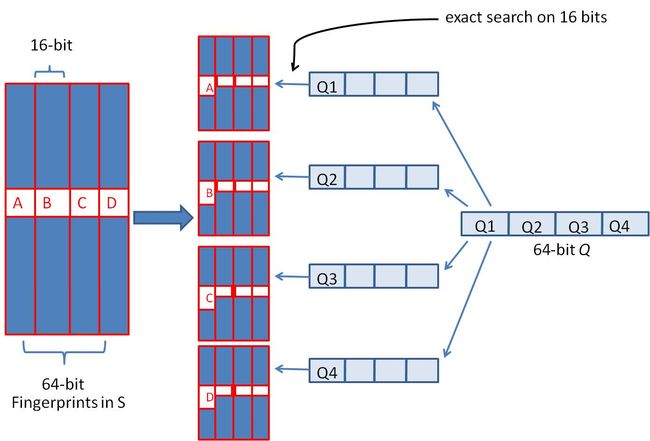
让我们来总结一下上述算法的实质： 
1、将64位的二进制串等分成四块 
2、调整上述64位二进制，将任意一块作为前16位，总共有四种组合，生成四份table 
3、采用精确匹配的方式查找前16位 
4、如果样本库中存有2^34（差不多10亿）的哈希指纹，则每个table返回2^(34-16)=262144个候选结果，大大减少了海明距离的计算成本 

我们可以将这种方法拓展成多种配置，不过，请记住，table的数量与每个table返回的结果呈此消彼长的关系，也就是说，时间效率与空间效率不可兼得，参看下图： 

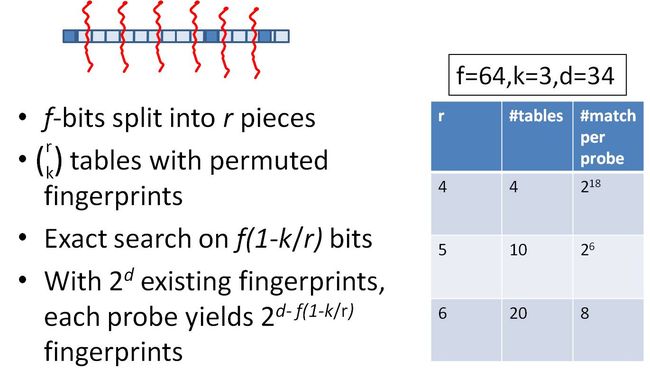
事实上，这就是Google每天所做的，用来识别获取的网页是否与它庞大的、数以十亿计的网页库是否重复。另外，simhash还可以用于信息聚类、文件压缩等。 

转自：http://grunt1223.iteye.com/blog/964564

Google 在 WWW2007 发表的一篇论文 “Detecting near-duplicates for web crawling”, 这篇文章中是要找到 duplicate 的网页，分两步 ： 

第一步 , 将文档这样的高维数据通过 Charikar's simhash 算法转化为一串比特位 . 对于 Google 的问题 , 
We experimentally validate that for a repository of 8 billion webpages, 64-bit simhash fingerprints and k = 3 are reasonable. 
就是对于 80 亿的文档 , 我们把每个文档转化为 64-bit 的 simhash fingerprints, 当两个 fingerprints 有k = 3 位不同时 , 我们就认为这两个文档不相同 .

Charikar's simhash is a dimensionality reduction technique . It maps high-dimensional vectors to small-sized fingerprints. 
其实 LSH 算法的基本原理就是 , 把一个多维空间上的点投影到一个平面上 , 当多维空间中的两个点在平面上的投影之间距离很近的时候 , 我们可以认为这两个在多维空间中的点之间的实际距离也很近 . 但是 , 你想象一下 , 你把一个三维球体中的两个点投影到一个随机平面上 , 当投影很靠近的时候, 其实那两个点不一定很靠近 , 也有可能离的很远 . 所以这儿可以把两个点投影到多个随机平面上 ,如果在多个随机平面上的投影都很靠近的话 , 我们就可以说这两个多维空间点之间实际距离很近的概率很大 . 这样就可以达到降维 , 大大的减少了计算量 .

算法过程如下 , 其实挺好理解的 
Computation: 
Given a set of features extracted from a document and their corresponding weights, we use simhash to generate an f-bit fingerprint as follows. 
We maintain an f-dimensional vector V, each of whose dimensions is initialized to zero. 
A feature is hashed into an f-bit hash value. 
These f bits (unique to the feature) increment/decrement the f components of the vector by the weight of that feature as follows: 
ü   if the i-th bit of the hash value is 1, the i-th component of V is incremented by the weight of that feature; 
ü   if the i-th bit of the hash value is 0, the i-th component of V is decremented by the weight of that feature. 
When all features have been processed, some components of V are positive while others are negative. The signs of components determine the corresponding bits of the final fingerprint. 
For our system, we used the original C++ implementation of simhash, done by Moses Charikar himself.

第二步 , HAMMING DISTANCE PROBLEM

第一步把所有文档都变成 64-bit 的 fingerprints, 那么面对几十亿的 fingerprints, 怎么样能快速找到和目标 fingerprint 相差 k 位的所有 fingerprint 了 . 
其实这就是个对于 hamming distance 的 KNN 问题 , 
Definition: Given a collection of f-bit fingerprints and a query fingerprint F, identify whether an existing fingerprint differs from F in at most k bits.

汉明距离 (hamming distance) 
在信息论中，两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数 
可见 , 对于 hamming 距离 , 不是简单的通过排序索引就可以解决的

说两个简单的方法 , 虽然不可行 , 但也是一种思路 
耗费时间的方法 
Build a sorted table of all existing fingerprints 
对于给定的 F, 找出所有 Hamming distance from F is at most k 的 fingerprint 然后去 table 里面搜索 ,看有没有 
For 64-bit _ngerprints and k = 3, we need C₆₄ ³ = 41664 probes. 这样查找时间太长了 .

耗费空间的方法 
还有个办法就是空间换时间 , 对现有的每个 fingerprints, 先事先算出所有和它 Hamming distance 小于 3 的情况 , 但这种方法预先计算量也太大了 , 如果现有 n 个 fingerprint, 就需要算 41664*n. 
可见用传统的方法是很难高效的解决这个问题的 .

那么怎么办 , 有什么办法能够在海量的 F bit 的向量中 , 迅速找到和查询向量 F ′ 只差 k bit 的向量集合了 
We now develop a practical algorithm that lies in between the two approaches outlined above: it is possible to solve the problem with a small number of probes and by duplicating the table of fingerprints by a small factor. 
我们需要一种介于上面两种比较极端的情况的方法 , 耗些时间 , 也耗些空间 , 但都不要太多 ......

设想一下对于 F bit, 可以表示 2^F 个数值 , 如果这儿我们完全随机产生 2^d 个 F bit 的数 , 当 d<<F 时 ,这些随机数值的高 d 位重复的应该不多 , 为什么 , 这些数值是完全随机产生的 , 所以应该相对均匀的分布在 2^F 大小的空间里 , 如果完全平均生成 2^d 个数 , 那么每个数的高 d 位都是不同 . 但是这儿是随机产生 , 所以会有些数的高 d 位是相同的 , 不过数量不会多 . 所以这边就可以把高 d 位作为计数器 ,或索引 . 这个假设是这个方法的核心 , 有了这个假设 , 不难想到下面怎么做 ...

首先对现有的所有 fingerprints 进行排序 , 生成有序的 fingerprints 表 
选择一个 d ′, 使得 |d ′-d| 的值很小 ( 就是说你选择的这个 d’ 和 d 只要差的不多 , 都可以 ), 因为表是有序的 , 一次检测就能够找出所有和 F ′ 在最高的 d ′ 位相同的指纹 , 因为 |d ′-d| 的值很小 , 所有符合要求的指纹数目也比较小 , 对于其中的每一个符合要求的指纹 , 我们可以轻易的判断出它是否和 F最多有 K 位不同 ( 这些不同很自然的限定在低 f-d ′ 位 ) 。

上面介绍的方法帮我们定位和 F 有 K 位不同的指纹 , 不过不同的位被限定在低 f-d ′ 位中。这对大部分情况来说是合适的 , 但你不能保证没有 k 位不同出现在高 d 位的情况 . 为了覆盖所有的情况 , 采用的方法就是使用一种排序算法 π, 把当前的 F bit 随机打乱 , 这样做的目的是使当前的高位 bit, 在打乱后出现在低位 bit, 然后我们再对打乱后的表排序 , 并把 F ′ 用相同的排序算法 π 打乱 
再重复我们上面的过程 , 来查找低 f-d ′ 位上 k 位不同的情况 
这样当我们多使用几种排序算法 π, 重复多次上面的过程 , 那么漏掉 ’k 位不同出现在高 d 位 ’ 的情况的概率就会相当的小 , 从而达到覆盖到所有情况

还有个问题 , 这儿的假设是 , 2^d 个数是随机产生的 . 那么我们这儿的 fingerprints 是基于 hash 算法产生的 , 本身具有很大的随机性 , 所以是符合这个假设的 . 这点原文 4.2 Distribution of Fingerprints 有相应的实验数据 .

假设 f=64,k=3, 那么近似网页的指纹最多有 3 位不同。假设我们有 8B=2³⁴ 的已有指纹 , 即 d=34 。 
我们可以生成 20 个有序排列表 ( 即使用 20 种不同的排列算法打乱原 fingerprint, 并生成有序表 ), 方法如下 ,  
把 64 位分成 6 块 , 分别是 11,11,11,11,10 和 10 位。共有 C(6,3)=20 种方法从 6 块中选择 3 块。对于每种选择 , 排列 π 使得选出的块中的位成为最高位 . d ′ 的值就是选出的块中的位数的总和。因此d ′=31,32, 或者 33 ( 和 d 差的不多 ). 平均每次检测返回最多 2^34~31 个排列后的指纹。实际应该不会很多

你也可以用 16 个表 , 或更少 , 但使用的表越少 , 必须 d 的取值也越少 , 这样最后需要验证的fingerprint 就越多 , 这儿就有个时空的平衡 , 时间和空间不可兼得 .

转自：http://blog.csdn.net/fxjtoday/article/details/6200257