编程珠玑第12章（取样问题）学习笔记

编程珠玑第12章（取样问题）学习笔记

――2013.01.17（By:Neicole）

零。大纲

1. 问题描述

2. 问题改进

3. 第一种方案――使用概率计算

4. 第二种方案――逐个随机插入

5. 第三种方案――内部乱序抽取

6. 我的收益

 

一。问题描述

 1. 名称：随机取样任务

 2. 输入：选区名列表，整数m

 3. 输出：随机选择的m个选区名列表

 PS: 1. 选区名常有几百个; 2.选区名为不超过12字符的字符串; 3. m常在20~40

 

二。问题改进

PS: 程序最终结果用上的输入数据只是部分（样品），若将全部输入放入内存再进行计算后取出结果，很可能会导致浪费掉大量的时间空间。

题目修改：

输入：m和n,使 0 < m < n ( m, n均为整数)

输出：m个随机整数的有序列表。（随机整数不允许重复）

 

三。第一种方案――使用概率计算

1. 伪代码

设：bigrand()能返回一个远大于n的函数

randint(i, j)能返回一个i...j范围内均匀选择的随机整数）

代码：

select = m
remaining = n
for i = [0, n)
  if (bigrand() % remaining) < select
      print i
      select—
  remaining--

　

 2.我的错误思考――错解本题

  初接触这伪代码，我想了很久，第一反应是，在伪代码中，n是数值大小，m(虽然在题意看来是数量，不过从程序看来)也是数值大小，而bigrand()也是数值大小，它们的大小是包含关系，如果按这样理解的话，如下图：

再套进这个算法，其中有一句　if (bigrand() % remaining) < select　，是不是就意味着我选择的数的大小都是得小于select这个数值的呢？如果是这样，存在很大问题，[m, n)的数无法取出，达不到题目从n里面取m个随机数的要求。

　　那么，现在问题是出在哪呢？

 

3. 解说――正解

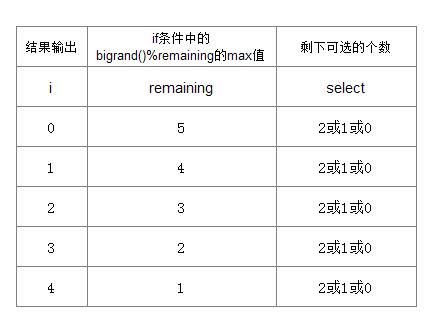
　　没错，select是在变小，但是，我们不可以忽略的一点是，结果输出的不是select而是变量i，问题的根本是if真正判断的是什么。观察代码时，我们可以将它们的几个变量同时观察，看它们间是否有联系。设m=2, n=5，那么，假设我们进入了伪代码中的循环语句，变量的变化如下所示：

　　这个算法的核心部分就是for里面的if语句，观察可知，进入循环条件，每过一轮循环，i的值就会加1，而select的值需要视情况而定，如果bigrand()%remaining的数值符合if条件，select的数值就会加1，否则不变。至于remaing数值随着i的增大而减小，这是碰巧吗？三个数值间的联系是什么？我们可以再看下图：

假设，我们是要将结果放入到m1、m2两个圈圈中，初始状态时，m1、m2都为empty，remaining为5，以后仍可能输出的i值为0、1、2、3、4五个；第1轮循环结束，可能输出的值剩下4个，而这也与remaing的值一样为4，此时，以后仍可能输出的i值为1、2、3、4四个，而在刚刚的第1循环，如果符合了循环内的if(bigrand() % remaining) < select条件，m2或m1会装入数值0（也就是说输出了i）；就这样进入一轮轮的循环，可以知道的是，remaining就是剩下还没有抽取的数的个数，每一轮循环，i会增大1，可以理解为我们随机选数的时候是从小到大计算数值是否符合条件，我们回顾原题，需要找出“有序”，“不重复”的随机数，这里的“随机”，我们可以从小到大筛选的原因是：我们是否进入的if条件，是一个“随机”得出的结果，而这个“随机”所关联的是一个“概率”，我们从概率的角度去思考这个问题，每个抽出的结果都能达到相同的“概率”时，即能达到“随机”。注意观察还没进入第1轮循环时，我们可取的数有5个，变量select（即图中的m1和m2的数目一共）为2，是否进入循环，我们就看（逻辑上）是否抽中0，而抽中随机数0（放入结果m1或m2）的概率为2/5，也就是select/k=m1/k+m2/k，那么我们如何能保证这个2/5呢？回看代码中的if (bigrand() % remaining) < select，已知bigrand()取出的是随机数，该随机数取模5，即bigrand()%remaining有可能的结果是0, 1, 2, 3, 4，五个结果出现的概率是均等的，再满足小于select=2的有0和1，也就是说，从这些均等的结果中，有1/5的(bingrand()%remaining=0)概率（可以放进m1）加上1/5的(bingrand()%remaining=1)概率(可以放进m2)，共2/5概率可以进入if条件执行if条件内的语句（放进m1或m2成为输出的结果），这样就保证了有2/5的概率可以取数值0作为最终结果，依此类推即可用均等的概率得出m1与m2 的值，输出结果，达到“随机”，“有序”的效果。

 

四。第二种方案――逐个随机插入

　　书中所讲，这思路来源于一个学生，他建议“复印选区列表，用切纸机将副本切成一个个含有选区名的纸片，然后将这些纸片放入一个纸袋中并摇乱，再从中抽取需要数目的纸片。”这是一个生活中可以用上的方法，我们常说，计算机来源于生活，果然如此，这也体现了书中所讲的“打破概念壁垒”的主题。

1. 伪代码

　　initialize set S to empty
    size = 0
    while size < m do
        t = bigrand() % n
        if t is not in S
          insert t into S
          size++
    print the elements of S in sorted order

2.问题联想与简要思路提要

　这代码看起来很简单，我将其理解为“取样放回再随机抽取”，也就是从一个集合中随机取一个数，每次取完后再将这个数放回集合中，如果下次取出的是同一个数则忽略这个结果，继续取数，直到取得满足条件的样品数目为此。每次都是从总数中取一个数，那么每个数被抽中的概率必然是均等的。满足题目“随机”的这个条件。

　我联想到的是我以前高中常做的一道题，脑海中很容易就能反映出这个场景“有一个布袋，里面装了n [0, 10)个标有号码白球，每次从袋子里面取出1个球，每次取球后将球放回，问从布袋里面取出号码xx的概率是多少？”虽然跟这题目所问的有些许不同，但是这场景实在是很像。解决题目时，联系生活。

 

五。第三种方案――内部乱序抽取

1.伪代码

　for i = [0, n)
    swap(i, randint(i, n-1) )   // randint(i, j)从i...j范围内均匀选择的随机整数的函数

 

2.问题联想与简要思路提要

  思路很简单，将集合内部的顺序打乱，然后再从这打乱中的集合取出m个数，取出来再进行排序，得出的即是结果。

　这种随机取样的方法让我想到了六合彩，我们是直接从集合内部搞出m个数即为随机抽样了，然后想满足题目条件的话就再进行排序就可以。

 

六。我的收益

　　这次对“取样问题”进行了探讨，刚开始没有想到可以将问题优化为从数值集合中取样的问题，更没有想到可以由“概率”的这个角度去思考这个“随机”的问题，又从书中解决问题的时候联想到生活现象，书本实在能引发我的思考，解决问题时，可以先试试想想本身的问题有没有可替换的方案，再可以想想方案还可以有哪些，思考方案的时候，还可以打破条条框框的概念，尝试用另一种思维去思考问题。