deep learning 自学习网络的Softmax分类器

   这一节我将跳过KNN分类器，因为KNN分类器分类时间效率太低，这一节讲Sparse autoencoder + softmax分类器。首先普及一下Sparse autoencoder网络，Sparse autoencoder可以看成一个3层神经网络，但是输入的数目和输出的个数相等。Sparse autoencoder的作用是提取特征，和PCA的功能有点类似，那么Sparse autoencoder是如何提取特征向量的呢？其实提取的特征就是隐含层的输出，首先来讲sparse autoencoder模型的图例如下：

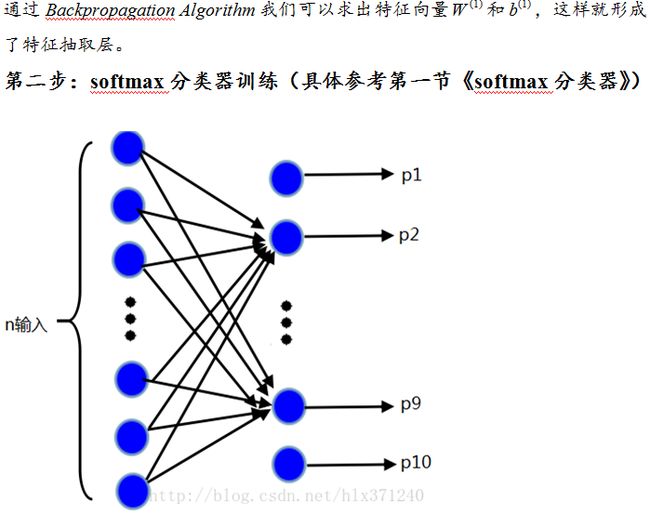
我们去掉输出层以后，隐含层的值就是我们需要求的特征值，假如有n个输入，隐含层有m个神经元，输出层也为n，那么此网络有m个特征值，隐含层的每个神经元与输入层的连线构成了特征向量。那么我们去掉输出层，就是输出特征值，然后再接上softmax分类器就形成了sparse autoencoder softmax分类器。特征值表示如下图：

下面分别讲Sparse autoencoder softmax分类器每一步：

第一步：Sparse autoencoder

         神经网络分为前馈和后馈

前馈网络

     一个神经网络是通过很多简单的神经元构成，下面是一个简单的神经网络。

后馈网络

   softmax分类器第一节有讲，sparse autoencoder网络训练用的是SD法，softmax分类器训练用的L-BFGS,具体可以参见《最优化计算方法》板块。

实验与结果

     还是以MNIST这个手写数字识别库为实验数据库，http://yann.lecun.com/exdb/mnist/

               MNIST数字识别库的图片是28×28大小尺寸，假如隐含层有200个神经元，那么在sparse autoencoder网络中就含有（784+1）*（200）+（200+1）*784=314584个参数。那么原来的softmax分类器需要784*10=7840个参数，现在经过特征抽取后只需要200*10=2000个参数。可以提取出这些数据的权值，权值转换成图片显示如下：

（1）sparse autoencoder网络损失函数随着迭代次数的曲线

最后通过softmax分类器可以得到识别率为97.21%，比直接用softmax分类器分类识别率高，直接softmax分类器的识别率为92.67%。具体代码见资源!

sparseautoencoder_softmax.m

%% ======================================================================
%  STEP 0: Here we provide the relevant parameters values that will
%  allow your sparse autoencoder to get good filters; you do not need to
%  change the parameters below.

inputSize  = 28 * 28;
numLabels  = 10;
hiddenSize = 200;
sparsityParam = 0.1; % desired average activation of the hidden units.
% (This was denoted by the Greek alphabet rho, which looks like a lower-case "p",
%  in the lecture notes).
lambda = 3e-3;       % weight decay parameter
beta = 3;            % weight of sparsity penalty term
maxIter = 450;
numClasses = 10;     % Number of classes (MNIST images fall into 10 classes)
lambda = 1e-4; % Weight decay parameter
itera_num=120;
Learningrate=0.6;
a=1;roi=0.5;c=0.6;m=10;
%% ======================================================================
%  STEP 1: Load data from the MNIST database
%
%  This loads our training and test data from the MNIST database files.
%  We have sorted the data for you in this so that you will not have to
%  change it.
% Load MNIST database files
images=loadMNISTImages('train-images.idx3-ubyte');
labels=loadMNISTLabels('train-labels.idx1-ubyte');
labels(labels==0) = 10;
%% ======================================================================
%  STEP 2: Train the sparse autoencoder
%  This trains the sparse autoencoder on the unlabeled training
%  images.
%  Randomly initialize the parameters
theta = initializeParameters(hiddenSize, inputSize);
%% sparseAutoencoder
W1 = reshape(theta(1:hiddenSize*inputSize), hiddenSize, inputSize);
W2 = reshape(theta(hiddenSize*inputSize+1:2*hiddenSize*inputSize), inputSize, hiddenSize);
b1 = theta(2*hiddenSize*inputSize+1:2*hiddenSize*inputSize+hiddenSize);
b2 = theta(2*hiddenSize*inputSize+hiddenSize+1:end);
% Cost and gradient variables (your code needs to compute these values).
% Here, we initialize them to zeros.

W1grad = zeros(size(W1));
W2grad = zeros(size(W2));
b1grad = zeros(size(b1));
b2grad = zeros(size(b2));
%%
Jcost = 0;%直接误差
Jweight = 0;%权值惩罚
Jsparse = 0;%稀疏性惩罚
[n m] = size(images);%m为样本的个数，n为样本的特征数
fprintf('%10s %10s','Iteration','cost','Accuracy');
fprintf('\n');
for i=1:maxIter
    %前向算法计算各神经网络节点的线性组合值和active值
    z2 = W1*images+repmat(b1,1,m);%注意这里一定要将b1向量复制扩展成m列的矩阵
    a2 = sigmoid(z2);
    z3 = W2*a2+repmat(b2,1,m);
    a3 = sigmoid(z3);
    % 计算预测产生的误差
    Jcost = (0.5/m)*sum(sum((a3-images).^2));
    
    %计算权值惩罚项
    Jweight = (1/2)*(sum(sum(W1.^2))+sum(sum(W2.^2)));
    
    %计算稀释性规则项
    rho = (1/m).*sum(a2,2);%求出第一个隐含层的平均值向量
    Jsparse = sum(sparsityParam.*log(sparsityParam./rho)+(1-sparsityParam).*log((1-sparsityParam)./(1-rho))); %损失函数的总表达式
    cost(i) = Jcost+lambda*Jweight+beta*Jsparse;
    %反向算法求出每个节点的误差值
    d3 = -(images-a3).*sigmoidInv(z3);
    sterm = beta*(-sparsityParam./rho+(1-sparsityParam)./(1-rho));%因为加入了稀疏规则项，所以
    %计算偏导时需要引入该项
    d2 = (W2'*d3+repmat(sterm,1,m)).*sigmoidInv(z2);
    %计算W1grad
    W1grad = W1grad+d2*images';
    W1grad = (1/m)*W1grad+lambda*W1;
    %计算W2grad
    W2grad = W2grad+d3*a2';
    W2grad = (1/m).*W2grad+lambda*W2;
    %计算b1grad
    b1grad = b1grad+sum(d2,2);
    b1grad = (1/m)*b1grad;%注意b的偏导是一个向量，所以这里应该把每一行的值累加起来
    %计算b2grad
    b2grad = b2grad+sum(d3,2);
    b2grad = (1/m)*b2grad;
    W1=W1-Learningrate*W1grad;
    W2=W2-Learningrate*W2grad;
    b1=b1-Learningrate*b1grad;
    b2=b2-Learningrate*b2grad;
    fprintf('%5d     %13.4e  \n',i,cost(i));
end
%-------------------------------------------------------------------

display_network(W1');
figure
plot(0:499, cost(1:500),'r--','LineWidth', 2);
%================================================
%STEP 3: 训练Softmax分类器
activation  = sigmoid(W1*images+repmat(b1,[1,size(images,2)]));
theta = 0.005 * randn(numClasses * hiddenSize, 1);%输入的是一个列向量
% Randomly initialise theta
theta = reshape(theta, numClasses, hiddenSize);%将输入的参数列向量变成一个矩阵
inputData = activation;
numCases = size(inputData, 2);%输入样本的个数
groundTruth = full(sparse(labels, 1:numCases, 1));%这里sparse是生成一个稀疏矩阵，该矩阵中的值都是第三个值1
%稀疏矩阵的小标由labels和1:numCases对应值构成

thetagrad = zeros(numClasses, hiddenSize);

p = weight(theta,inputData);
Jcost(1) = -1/numCases * groundTruth(:)' * log(p(:)) + lambda/2 * sum(theta(:) .^ 2);
thetagrad = -1/numCases * (groundTruth - p) * inputData' + lambda * theta;
B=eye(numClasses);
H=-inv(B);
d1=H*thetagrad;
theta_new=theta+a*d1;
theta_old=theta;
fprintf('%10s %10s %15s %15s %15s','Iteration','cost','Accuracy');
fprintf('\n');
%% Training
for i=2:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数
    a=1;
    theta_new=reshape(theta_new, numClasses,hiddenSize);
    theta_old=reshape(theta_old,numClasses,hiddenSize);
    p=weight(theta_new,inputData);
    Mp=weight(theta_old,inputData);
    Jcost(i)=-1/numCases * groundTruth(:)' * log(p(:)) + lambda/2 * sum(theta_new(:) .^ 2);
    thetagrad_new = -1/numCases * (groundTruth - p) * inputData' + lambda * theta_new;
    thetagrad_old = -1/numCases * (groundTruth - Mp) * inputData' + lambda * theta_old;
    thetagrad_new=reshape(thetagrad_new,numClasses*hiddenSize,1);
    thetagrad_old=reshape(thetagrad_old,numClasses*hiddenSize,1);
    theta_new=reshape(theta_new,numClasses*hiddenSize,1);
    theta_old=reshape(theta_old,numClasses*hiddenSize,1);
    M(:,i-1)=thetagrad_new-thetagrad_old;
    BB(:,i-1)=theta_new-theta_old;
    roiJ(i-1)=1/(M(:,i-1)'*BB(:,i-1));
    gamma=(BB(:,i-1)'*M(:,i-1))/(M(:,i-1)'*M(:,i-1));
    HK=gamma*eye(hiddenSize*numClasses);
    r=lbfgsloop(i,m,HK,BB,M,roiJ,thetagrad_new);
    d=-r;
    d=reshape(d,numClasses,hiddenSize);
    theta_new=reshape(theta_new,numClasses,hiddenSize);
    theta_old=theta_new;
    theta_new = theta_new + a*d;
    %% test the accuracy
    fprintf('%5d     %13.4e \n',i,Jcost(i));
end
plot(0:119, Jcost(1:120),'r-o','LineWidth', 2);
testData = loadMNISTImages('t10k-images.idx3-ubyte');
labels1 = loadMNISTLabels('t10k-labels.idx1-ubyte');
labels1(labels1==0) = 10;

test  = sigmoid(W1*testData+repmat(b1,[1,size(testData,2)]));
inputDatatest = test;
pred = zeros(1, size(inputDatatest, 2));
[nop,pred]=max(theta_new*inputDatatest);
acc = mean(labels1(:) == pred(:));
acc=acc * 100

========================================================================================

第三节：从自我学习到深层网络学习

========================================================================================

                                                                      怀柔风光