前向动力学与反向动力学是骨骼动画中很重要的方法,那么它的原理和实现究竟是怎样的呢,我写了一篇关于前向动力学与反向动力学的教程,希望对大家有帮助!
一、前向动力学的特点:
1、具有层次的骨骼结构,比如说当我们举起手臂的时候,我们的手肘跟着运动,手腕跟着手肘运动,手指跟着手腕运动,这就是一个典型的具有层次的骨骼运动,也就说,当父骨骼运动时,所有的子骨骼也随之运动
2、每一根骨骼都是由定义在其父骨骼关节坐标空间中的旋转角度ri和固定的位移ti决定的
设R={r0, r1, r2, r3,……}
那么骨骼链中的最末端的骨骼的位置E(Ex,Ey,Ez)(终端效应)
E=f(R)
那么在一般2D情况下
考虑以下的骨骼链:
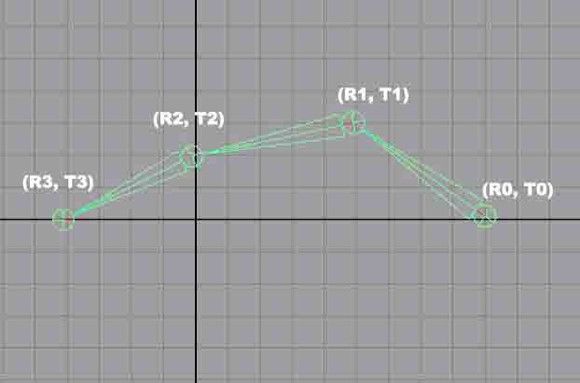
可以看见骨骼链的末端骨骼的位置和旋转就是由r0, r1, r2, r3和t0, t1, t2, t3决定的,由于t0, t1, t2, t3是固定的,因此实际是仅有r0, r1, r2, r3所决定。那么我们可以简单研究一下二维平面上的骨骼旋转,请看下图:
设骨骼1,骨骼2,骨骼3的长度分别为L1,L2, L3
设骨骼1,骨骼2,骨骼3的位置二维向量分别为T1,T2, T3
设骨骼1,骨骼2,骨骼3的夹角分别为R1,R2, R3
关节2的位置为T2=(T1.x+L1*cos(R1),T1.y+L1*sin(R1))
关节3的位置为T3=(T2.x+-L2*cos(R2-R1),T2.y+L2*sin(R2-R1))
终端感应器的位置为E=(T2.x+L3*cos(R3-R2-R1),T2.y+L3*sin(R3-R2-R1))
二、反向动力学
反向动力学
前向动力学是给定一系列骨骼的状态值r0, r1, r2, r3和t0, t1, t2, t3那么最终骨骼的形态就决定了,终端感应器即最后一根骨骼的位置和旋转也就确定了。但有时候在实际应用中往往是这样一种情况,即确定了一个目标位置,让骨骼通过旋转,使得最后终端感应器能够处于目标位置之上。那么在中情况下就需要进行反向动力学求解了。即已知E(Ex,Ey,Ez),求R ={r0, r1, r2, r3,。。。。}
在前向动力学中E=f(R)
那么在反向动力学中R=f-1(E)
反向动力学的求解通常有那么几种方法:
解析求解:通过对方程式进行直接求解,并选择最优解,但在应用中并不可行
数值分析法:通常代价昂贵,不精确,但是在应用中往往是可行的唯一方法
三种常用方法:
1、雅克比矩阵法(数值分析法)
2、圆柱坐标法(数值分析法)
3、三角函数法(解析求解)
雅克比矩阵法
雅克比矩阵法是由整个系统各个参数R ={r0, r1, r2, r3,。。。。}的偏导数əR ={ər0, ər1, ər2, ər3,。。。。}
那么当系统中R ={r0, r1, r2, r3,。。。。}发生ΔR ={Δr0, Δr1, Δ r2, Δr3,。。。。}
变化时,对应E发生的变化ΔE= əRΔR,ΔE={ΔEx,ΔEy,ΔEz}
实际上,这里只是线性近似,为什么呢,请看下图
雅克比矩阵为:
əEx/r0 əEx/r1 … əEx/rn
j= əEy/r0 əEy/r1 … əEy/rn
əEz/r0 əEz/r1 … əEz/rn
已知ΔE={ΔEx,ΔEy,ΔEz}求ΔR ={Δr0, Δr1, Δ r2, Δr3,。。。。},在J为方型矩阵的情况下,ΔR=J-1ΔE, J-1为雅克比矩阵J的逆矩阵
雅克比矩阵的问题:
1、如果系统是个高约束系统或者过低约束系统
2、雅克比矩阵不可逆,即系统无解
3、雅克比矩阵不一定为方阵
为了解决这个问题:
我们引入矩阵J+= (JT J)-1 JT
(JT J)-1是方阵,并且可逆,那么我们就可以了利用(JT J)-1,而且这是可行的,为什么呢,我们先看看此公式的推导:
JΔR=ΔE
那么J JTΔR= JTΔE,两边同时乘上(J JT)-1,最后得到
ΔR=(J JT)-1 JTΔE,取J+= (JT J)-1 JT
...