JOJ 1114 The Maze 种子填充算法
题目见: http://acm.jlu.edu.cn/joj/showproblem.php?pid=1114
题目描述比较短,直接把原文贴上来:
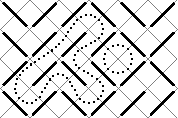
By filling a rectangle with slashes (/) and backslashes (/), you can generate nice little mazes. Here is an example:
As you can see, paths in the maze cannot branch, so the whole maze only contains cyclic paths and paths entering somewhere and leaving somewhere else. We are only interested in the cycles. In our example, there are two of them.
Your task is to write a program that counts the cycles and finds the length of the longest one. The length is defined as the number of small squares the cycle consists of (the ones bordered by gray lines in the picture). In this example, the long cycle has length 16 and the short one length 4.
这个题目当时有两种思路:种子填充;直接对输入的迷宫形式进行分析。自己使用比较直观简单的种子填充算法。
因为输入的迷宫形式中只有墙 ( 用 ’/’ 或者 ’/’ 表示 ) 。所以为了方便地进行填充需要用输入的迷宫形式构造一个可以在其中行走的迷宫 ( 即即有墙也有通道的迷宫 ) 。根据题目描述中的那张图的启示,用一个 2*2 的小方块的两条对角线表示墙壁。例如对于输入:
//////
//////
//////
//////
构造出来与它对应的迷宫就是:
上面,两个相同的数字表示它们的连线是一堵墙。
在这个构造好的迷宫中行走,实际上走的是顶点而不是小方格。即在构造出来的迷宫中,一条能够行走的路径是由空白方格的对角线组成而不是由空白方格组成。路径的长度就是对角线的数目 ( 路径中的对角线是指 1*1 方格的对角线 , 2*2 方格的有数字的对角线是墙壁 ) 。
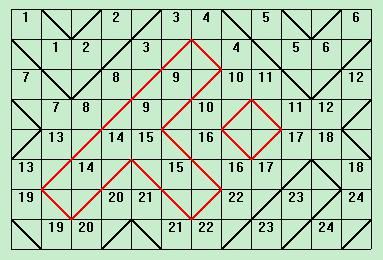
那么种子填充的思路的就是:依次从所有外围的顶点开始进行填充,这样可以找到所有非回路的路径。然后对每个不在某个墙壁上的顶点 ( 即不在某个 2*2 方块的对角线上 ) 进行种子填充,这样就是找到所有回路。例如对上面构造出来的迷宫进行填充的结果如下:
其中黑线连接的路径表示非回路的路径。红线连接的路径表示回路。很容易看出,共有两条回路,最长的一条回路长度为 16 。
为了写代码的方便,最好在构造的迷宫外围加上一圈非空的方格,这样就不用在种子填充的代码中判断越界的情况。
上面两张图片是使用 MFC 写程序画出来的。
算法中种子填充部分的代码如下:
void floodfill ( int x, int y) {
if (maze[x-1][y]>0 && maze[x-1][y]==maze[x][y-1]) return ;
if (maze[x-1][y-1]>0 && maze[x-1][y-1]==maze[x][y]) return ;
if (maze[x-1][y-1] == EMPTY) {
if (!(maze[x-1][y-2] > 0 && maze[x-1][y-2] == maze[x-2][y-1])) {
maze[x-1][y-1] = curPath;
cycleLen ++;
floodfill(x-1,y-1);
}
}
if (maze[x-1][y] == EMPTY) {
if (!(maze[x-2][y] > 0 && maze[x-2][y] == maze[x-1][y+1])) {
maze[x-1][y] = curPath;
cycleLen ++;
floodfill(x-1, y+1);
}
}
if (maze[x][y] == EMPTY) {
if (!(maze[x][y+1] > 0 && maze[x][y+1] == maze[x+1][y])) {
maze[x][y] = curPath;
cycleLen ++;
floodfill(x+1,y+1);
}
}
if (maze[x][y-1] == EMPTY) {
if (!(maze[x][y-2] > 0 && maze[x][y-2] == maze[x+1][y-1])) {
maze[x][y-1] = curPath;
cycleLen ++;
floodfill(x+1,y-1);
}
}
}