斯坦福大学机器学习——支持向量机(1)
首次听说SVM是在实验室的科研进展报告上听杨宝华老师提到过,当时听得云里雾里,觉得非常的高大上。随后在辜丽川老师的人工智能作业上我也选择介绍SVM。但都是浅显的认识,没有继续深入。最近看了Andrew Ng的讲义和v_JULY_v大神的博文《支持向量机通俗导论(理解SVM的三层境界)》才算对基本概念有所了解。
简介
SVM是Support Vector Machine的缩写,中文翻译为“支持向量机”,由Vapnik在1992年首次提出,是一种监督学习分类算法。它将n维空间上的点用n-1维超平面分隔,并且使得不同类型的点到该超平面的距离最大。
一、 决策边界(Decision boundary)
在处理机器学习的分类问题时,一条超曲面将样本划分为两个不同的部分,每个部分即是各代表一个类,而这条超曲面就称为样本的决策边界。
在logistic回归中,样本被线性方程![]() 分为两个不同的类,再将
分为两个不同的类,再将![]() 该映射至sigmoid函数上得到
该映射至sigmoid函数上得到![]() 。当模型建立后,输入新的样本,当
。当模型建立后,输入新的样本,当![]() 时(或者时
时(或者时![]() ),我们认为该样本属于一个类,而时,样本属于另外一个类。
),我们认为该样本属于一个类,而时,样本属于另外一个类。
下面两个图就是两类样本被一个线性决策边界划分成两个部分,边界的两侧样本分别属于不同的类。这个决策边界是可用线性函数表示,因此为线性决策边界。
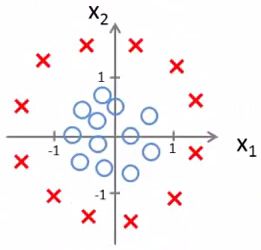
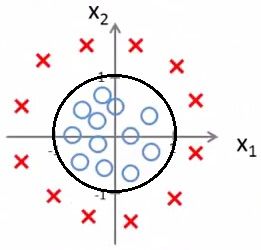
而对于下面这样两类数据,它们的决策边界就不能用线性函数表示了,因此为线性不可分。
二、 分类器
我们假设类标签值![]() ,定义分类器为:
,定义分类器为:
当![]() 时,
时,![]() ,否则。其中,
,否则。其中,![]() 表示关于x的线性函数,而b表示改线性函数的常数项。
表示关于x的线性函数,而b表示改线性函数的常数项。
通过这个分类器,可以将n维的样本通过超平面![]() 分为+1和-1两类。但是将样本分为两类的决策边界可以有无数种,我们的目标是寻求间隔最大的超平面决策边界。
分为+1和-1两类。但是将样本分为两类的决策边界可以有无数种,我们的目标是寻求间隔最大的超平面决策边界。
三、 函数间隔和几何间隔
(1)函数间隔(functional margin)
假定的训练样本为![]() ,那么定义点
,那么定义点![]() 的函数间隔为:
的函数间隔为:
如果![]() ,我们期望为尽可能大的正数,以保证函数间隔尽可能大;相反,若
,我们期望为尽可能大的正数,以保证函数间隔尽可能大;相反,若![]() 我们期望为尽可能大的负数,以保证函数间隔尽可能大。
我们期望为尽可能大的负数,以保证函数间隔尽可能大。
我们定义所有样本的最小函数间隔为:
然而,若将w和b的值都等比例扩大,比如都扩大3倍,变为3w和3b,那么决策边界将没有变化,而相应的函数间隔却扩大了3倍,因此,仅仅利用函数间隔不能客观有效的度量各点和分隔超平面的距离。我们可以通过将法向量加以约束的方法解决上面存在的问题。下面引入几何间隔:
(2)几何间隔
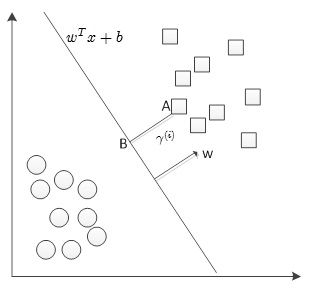
我们通过下图介绍几何间隔:
假设样本的分隔平面为![]() ,如果样本A(特征值为
,如果样本A(特征值为![]() )做垂线至分隔平面交于点B,那么,线段AB长度即为点
)做垂线至分隔平面交于点B,那么,线段AB长度即为点![]() 的几何间隔,记作
的几何间隔,记作![]() 。下面推导
。下面推导![]() 的值:
的值:
w为垂直于分隔超平面的法向量,那么![]() 就表示单位法向量(其中
就表示单位法向量(其中![]() 表示向量w的二阶范数)。上图中B点的坐标可以表示为:
表示向量w的二阶范数)。上图中B点的坐标可以表示为:![]() ,又因为B点在该超平面上,从而满足:
,又因为B点在该超平面上,从而满足:
由上式可得:
但是此时求出的![]() 值可能为正也可能为负(由的正负性决定),又由于
值可能为正也可能为负(由的正负性决定),又由于![]() ,因此,稍加修正即得到
,因此,稍加修正即得到![]() 的绝对值:
的绝对值:
假如令![]() ,那么函数间隔与几何间隔相等。这是,即使将w和b按比例扩大或者缩小,
,那么函数间隔与几何间隔相等。这是,即使将w和b按比例扩大或者缩小,![]() 的值不会因此改变。
的值不会因此改变。
最后定义所有样本的最小几何间隔为:
四、最大间隔分类器
假设训练集线性可分,我们的目的是通过某种优化方法,使得超平面距离数据点的几何间隔尽可能大,以使分类的确信度更高。
根据要求,可以将需要优化的问题表达成以下目标函数和约束条件:
![]()
![]()
若需要使几何间隔![]() 最大,要确保训练集中所有点到超平面的几何间隔都不小于
最大,要确保训练集中所有点到超平面的几何间隔都不小于![]() ,而
,而![]() 为了确保函数间隔和几何间隔相等。
为了确保函数间隔和几何间隔相等。
如果上述优化问题可以直接得出,那么事情就已经完成了。然而![]() ,是一个非凸约束,目标函数不能直接求出,因此,我们只能将目标函数和约束条件转换为以下对偶问题:
,是一个非凸约束,目标函数不能直接求出,因此,我们只能将目标函数和约束条件转换为以下对偶问题:
![]()
此时,以上的优化问题就转化为了一个二次的目标函数和线性的约束条件,属于凸二次规划问题。(东西太多了,先写到这里,下一篇将介绍拉格朗日对偶问题、KKT条件和优化分类器)。