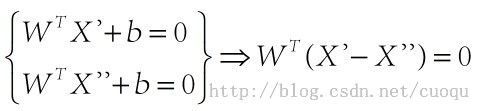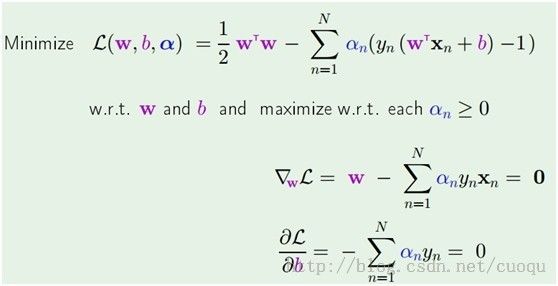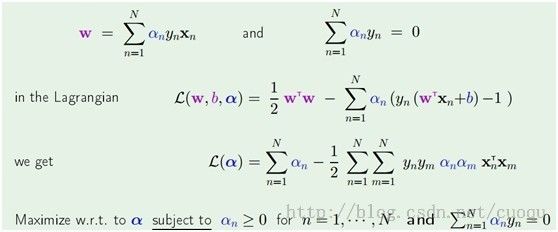机器学习理论与实战(五)支持向量机
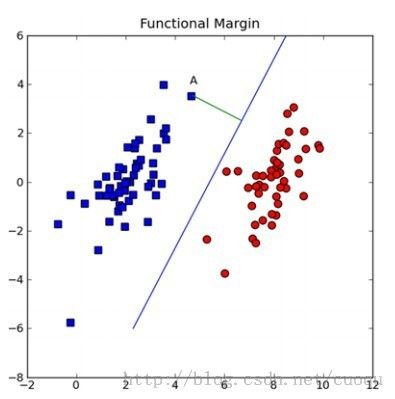
做机器学习的一定对支持向量机(support vector machine-SVM)颇为熟悉,因为在深度学习出现之前,SVM一直霸占着机器学习老大哥的位子。他的理论很优美,各种变种改进版本也很多,比如latent-SVM, structural-SVM等。这节先来看看SVM的理论吧,在(图一)中A图表示有两类的数据集,图B,C,D都提供了一个线性分类器来对数据进行分类?但是哪个效果好一些?
(图一)
可能对这个数据集来说,三个的分类器都一样足够好了吧,但是其实不然,这个只是训练集,现实测试的样本分布可能会比较散一些,各种可能都有,为了应对这种情况,我们要做的就是尽可能的使得线性分类器离两个数据集都尽可能的远,因为这样就会减少现实测试样本越过分类器的风险,提高检测精度。这种使得数据集到分类器之间的间距(margin)最大化的思想就是支持向量机的核心思想,而离分类器距离最近的样本成为支持向量。既然知道了我们的目标就是为了寻找最大边距,怎么寻找支持向量?如何实现?下面以(图二)来说明如何完成这些工作。
(图二)
假设(图二)中的直线表示一个超面,为了方面观看显示成一维直线,特征都是超面维度加一维度的,图中也可以看出,特征是二维,而分类器是一维的。如果特征是三维的,分类器就是一个平面。假设超面的解析式为 ,那么点A到超面的距离为 ,下面给出这个距离证明:(图三)
在(图三)中,青色菱形表示超面,Xn为数据集中一点,W是超面权重,而且W是垂直于超面的。证明垂直很简单,假设X’和X’’都是超面上的一点,
,因此W垂直于超面。知道了W垂直于超面,那么Xn到超面的距离其实就是Xn和超面上任意一点x的连线在W上的投影,如(图四)所示:
(图四)
而(Xn-X)在W上的投影![]() 可通过(公式一)来计算,另外(公式一)也一并完成距离计算:
可通过(公式一)来计算,另外(公式一)也一并完成距离计算:
(公式一)
注意最后使用了配项法并且用了超面解析式 才得出了距离计算。有了距离就可以来推导我们刚开始的想法:使得分类器距所有样本距离最远,即最大化边距,但是最大化边距的前提是我们要找到支持向量,也就是离分类器最近的样本点,此时我们就要完成两个优化任务,找到离分类器最近的点(支持向量),然后最大化边距。如(公式二)所示:(公式二)
大括号里面表示找到距离分类超面最近的支持向量,大括号外面则是使得超面离支持向量的距离最远,要优化这个函数相当困难,目前没有太有效的优化方法。但是我们可以把问题转换一下,如果我们把 大括号里面的优化问题固定住,然后来优化外面的就很容易了,可以用现在的优化方法来求解,因此我们做一个假设,假设大括号里的分子 等于1,那么我们只剩下优化W咯,整个优化公式就可以写成(公式三)的形式:(公式三)
这下就简单了,有等式约束的优化,约束式子为 ,这个约束等式背后还有个小窍门,假设我们把样本 Xn 的标签设为 1 或者 -1 ,当 Xn 在超面上面(或者右边)时,带入超面解析式得到大于 0 的值,乘上标签 1 仍然为本身,可以表示离超面的距离;当 Xn 在超面下面(或者左边)时,带入超面解析式得到小于 0 的值,乘上标签 -1 也是正值,仍然可以表示距离,因此我们把通常两类的标签 0 和 1 转换成 -1 和 1 就可以把标签信息完美的融进等式约束中,(公式三)最后一行也体现出来咯。下面继续说优化 求解(公式四)的方法,在最优化中,通常我们需要求解的最优化问题有如下几类:(i)无约束优化问题,可以写为:
min f(x);
(ii)有等式约束的优化问题,可以写为:
min f(x),
s.t. h_i(x) = 0; i =1, ..., n
(iii)有不等式约束的优化问题,可以写为:
min f(x),
s.t. g_i(x) <= 0; i =1, ..., n
h_j(x) = 0; j =1,..., m
对于第(i)类的优化问题,常常使用的方法就是Fermat定理,即使用求取f(x)的导数,然后令其为零,可以求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解。
对于第(ii)类的优化问题,常常使用的方法就是拉格朗日乘子法(LagrangeMultiplier),即把等式约束h_i(x)用一个系数与f(x)写为一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为零,可以求得候选值集合,然后验证求得最优值。
对于第(iii)类的优化问题,常常使用的方法就是KKT条件。同样地,我们把所有的等式、不等式约束与f(x)写为一个式子,也叫拉格朗日函数,系数也称拉格朗日乘子,通过一些条件,可以求出最优值的必要条件,这个条件称为KKT条件。
而(公式三)很明显符合第二类优化方法,因此可以使用拉格朗日乘子法来对其求解,在求解之前,我们先对(公式四)做个简单的变换。最大化||W||的导数可以最小化||W||或者W’W,如(公式四)所示:
(公式四)
套进拉格朗日乘子法公式得到如(公式五)所示的样子:
(公式五)
在(公式五)中通过拉格朗日乘子法函数分别对W和b求导,为了得到极值点,令导数为0,得到
,然后把他们代入拉格朗日乘子法公式里得到(公式六)的形式:
(公式六)
(公式六)后两行是目前我们要求解的优化函数,现在只需要做个二次规划即可求出alpha,二次规划优化求解如(公式七)所示:
(公式七)
通过(公式七)求出alpha后,就可以用(公式六)中的第一行求出W。到此为止,SVM的公式推导基本完成了,可以看出数学理论很严密,很优美,尽管有些同行们认为看起枯燥,但是最好沉下心来从头看完,也不难,难的是优化。二次规划求解计算量很大,在实际应用中常用SMO(Sequential minimal optimization)算法,SMO算法打算放在下节结合代码来说。
参考文献:
[1]machine learning in action. Peter Harrington
[2] Learning From Data. Yaser S.Abu-Mostafa
转载请注明来源:http://blog.csdn.net/cuoqu/article/details/9286099