计算思维(2)- 滤波
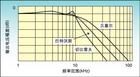
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。 在振幅的对数对角频率的波特图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
一阶巴特沃斯滤波器的衰减率为每倍频6分贝,每十倍频20分贝。二阶巴特沃斯滤波器的衰减率为每倍频12分贝、三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。巴特沃斯滤波器的振幅对角频率
单调下降,并且也是唯一的无论阶数,振幅对角频率曲线都保持同样的形状的滤波器。只不过滤波器阶数越高,在阻频带振幅衰减速度越快。其他滤波器高阶的振幅对角频率图和低级数的振幅对角频率有不同的形状。
b,a=scipy.signal.iirdesign(wp=0.2,ws=0.1,gstop=60,gpass=1,ftype='butter')
filtered=scipy.signal.lfilter(b,a,data)
scipy.io.wavfile.write('filtered.wav',sample_rate,filtered.astype(data.dtype))
索贝尔算子(Sobel operator)是
图像处理中的算子之
主要用作
边缘检测
。在技术上,它是一离散性
差分
算子,用来运算图像亮度函数的梯度之近似值。在图像的任何一点使用此算子,将会产生对应的梯度矢量或是其法矢量
该算子包含两组3x3的
矩阵,分别为横向及纵向,将之与图像作平面
卷积,即可分别得出横向及纵向的亮度
差分近似值。如果以A代表原始图像,Gx及Gy分别代表经横向及纵向
边缘检测的图像,其公式如下:
图像的每一个像素的横向及纵向梯度近似值可用以下的
公式结合,来计算梯度的大小。
然后可用以下公式计算梯度方向。
在以上例子中,如果以上的角度Θ等于零,即代表图像该处拥有纵向边缘,左方较右方暗。
在边缘检测中,常用的一种模板是Sobel 算子。Sobel 算子有两个,一个是检测水平边缘的 ;另一个是检测垂直边缘的 。与Prewitt算子相比,Sobel算子对于象素的位置的影响做了加权,可以降低边缘模糊程度,因此效果更好。
Sobel算子另一种形式是各向同性Sobel(Isotropic Sobel)算子,也有两个,一个是检测水平边缘的 ,另一个是检测垂直边缘的 。各向同性Sobel算子和普通Sobel算子相比,它的位置加权系数更为准确,在检测不同方向的边沿时梯度的幅度一致。将Sobel算子矩阵中的所有2改为根号2,就能得到各向同性Sobel的矩阵。
由于 Sobel算子是滤波算子的形式,用于提取边缘,可以利用快速 卷积函数, 简单有效,因此应用广泛。美中不足的是,Sobel算子并没有将图像的主体与背景严格地区分开来,换言之就是Sobel算子没有基于 图像灰度进行处理,由于Sobel算子没有严格地模拟人的视觉生理特征,所以提取的图像轮廓有时并不能令人满意。 在观测一幅图像的时候,我们往往首先注意的是图像与背景不同的部分,正是这个部分将主体突出显示,基于该理论,我们给出了下面阈值化轮廓提取算法,该算法已在 数学上证明当像素点满足正态分布时所求解是最优的。
x轴
sobelx=scipy.ndimage.sobel(lena,axis=0,mode='constant')
y轴
sobely=sciypy.ndimage.soble
(lena,axis=1,mode='constant')
使用sobel滤波
default=scipy.ndimage.sobel(lena)