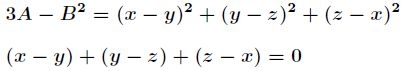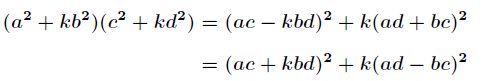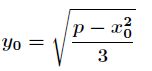表为平方和终极版
声明:本片文章在我的草稿箱已经尘封很久了,初稿时间是2014年9月8日,如下
为什么我一直没有发出来呢? 是因为我的代码没有得到Yes,由于参加工作了,以后来研究的时间相对
少点,现在发表出来希望有高手能指出错误之处,共同进步,谢谢!
以前写过表为平方和初级版,链接为http://blog.csdn.net/acdreamers/article/details/10083393,
主要的问题是求形如![]() 丢番图方程的解。今天我将来探讨另一类丢番图方程的解,即的
丢番图方程的解。今天我将来探讨另一类丢番图方程的解,即的
解。当然,我们需要先对素因子分解,得到形如的方程,其中为奇素数。根据![]() 的不同,方程有
的不同,方程有
解的条件也不一样。比如
(1)![]() 时,有解的条件是
时,有解的条件是
(2)![]() 时,有解的条件是
时,有解的条件是![]()
接下来,我会重点以一道经典题目的解析来说明此类丢番图方程在竞赛中的应用。
题目:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3815
题意:给定两个正整数![]() 和
和![]() ,其中
,其中![]() 和,输出所有满足条件的三元组,并且
和,输出所有满足条件的三元组,并且
输出数据满足条件。
分析:本题是2014年亚洲区域赛网络预选赛(牡丹江赛区)的G题。然而现场AC率为0,接下来进行详细探讨
首先根据已知条件,我们可以得到如下
再令,则有
继续消去![]() ,得到
,得到
![]()
令![]() ,得到
,得到![]() ,再将
,再将![]() 素因子分解,分别求出解,
素因子分解,分别求出解,
然后合并即可,合并的时候跟丢番图方程![]() 的合并类似,如下
的合并类似,如下
现在的关键问题是如何求解丢番图方程![]() ,其中
,其中![]() 为奇素数,此处。
为奇素数,此处。
那么有解的条件是![]() ,并且解唯一,求解
,并且解唯一,求解![]() 和的方法跟上次类似,具体步骤如下
和的方法跟上次类似,具体步骤如下
(1)先求出同余方程的最小正整数解![]()
(2)对和![]() 进行辗转相除运算,记录每次的余数为
进行辗转相除运算,记录每次的余数为![]() (注意第一次的余数为
(注意第一次的余数为![]() ),当满足条件
),当满足条件![]()
时停止,此时的![]() 就是
就是![]() ,而可以通过
,而可以通过![]() 得到,即
得到,即
代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#include <vector>
#include <math.h>
#include <set>
#include <map>
using namespace std;
const int N = 255;
const int M = 200005;
typedef long long LL;
char str[N];
LL a[N];
struct Pair
{
LL x, y;
bool operator < (const Pair &a) const
{
if(a.x == x) return a.y > y;
return a.x > x;
}
};
Pair node[M];
struct Res
{
LL x, y, z;
bool operator < (const Res &a) const
{
if(a.x == x && a.y == y) return a.z > z;
if(a.x == x) return a.y > y;
return a.x > x;
}
};
set<Pair> Set;
set<Res> _Set;
set<Pair> Mem;
vector<LL> vec;
int sign[4][2] = {{-1, -1}, {-1, 1}, {1, -1}, {1, 1}};
int _sign[2][2] = {{-1, 1}, {1, -1}};
LL multi(LL a, LL b, LL m)
{
LL ans = 0;
a %= m;
while(b)
{
if(b & 1)
{
ans = (ans + a) % m;
b--;
}
b >>= 1;
a = (a + a) % m;
}
return ans;
}
LL quick_mod(LL a, LL b, LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = multi(ans, a, m);
b--;
}
b >>= 1;
a = multi(a, a, m);
}
return ans;
}
struct T
{
LL p, d;
};
LL w;
T multi_er(T a, T b, LL m)
{
T ans;
ans.p = (multi(a.p, b.p, m) + multi(multi(a.d, b.d, m), w, m)) % m;
ans.d = (multi(a.p, b.d, m) + multi(a.d, b.p, m)) % m;
return ans;
}
T power(T a, LL b, LL m)
{
T ans;
ans.p = 1;
ans.d = 0;
while(b)
{
if(b & 1)
{
ans = multi_er(ans, a, m);
b--;
}
b >>= 1;
a = multi_er(a, a, m);
}
return ans;
}
LL Legendre(LL a, LL p)
{
return quick_mod(a, (p - 1) >> 1, p);
}
LL Work(LL n, LL p)
{
if(p % 3 != 1) return -1;
LL a = -1, t;
while(1)
{
a = rand() % p;
t = a * a - n;
w = (t % p + p) % p;
if(Legendre(w, p) + 1 == p) break;
}
T tmp;
tmp.p = a;
tmp.d = 1;
T ans = power(tmp, (p + 1) >> 1, p);
return ans.p;
}
LL Solve(LL n, LL p, LL &_x, LL &_y)
{
LL x = Work(n, p);
if(x == -1)
return -1;
if(x >= p - x)
x = p - x;
LL t = p;
LL r = x;
LL limit = (LL)sqrt(1.0 * p);
while(r > limit)
{
x = r;
r = t % x;
t = x;
}
_x = r;
_y = (LL)sqrt((p - r * r) / 3);
return 0;
}
void Prepare(char str[], LL a[], int &cnt)
{
cnt = 0;
LL ans = 0;
bool flag = 0;
int len = strlen(str);
for(int i=0; i<=len; i++)
{
if(str[i] >= '0' && str[i] <= '9')
ans = ans * 10 + str[i] - '0';
else if(str[i] == '-')
flag = 1;
else
{
if(flag) ans = -ans;
a[cnt++] = ans;
ans = 0;
flag = 0;
}
}
}
bool getData(Pair node[], LL a[], int &cnt)
{
int k = 0;
int _cnt = 0;
for(int i = 0; i < cnt; i++)
{
if(a[i] == 2) k++;
if(k == 2)
{
node[_cnt].x = 1;
node[_cnt].y = 1;
_cnt++;
k = 0;
}
if(a[i] > 2)
{
LL x, y;
int ans = Solve(-3, a[i], x, y);
if(ans == -1) return false;
node[_cnt].x = x;
node[_cnt].y = y;
_cnt++;
}
}
cnt = _cnt;
if(k == 1) return false;
return true;
}
void dfs(int dept, int cnt, Pair ans)
{
if(dept == cnt - 1)
{
Set.insert(ans);
return;
}
for(int i = 0; i < 4; i++)
{
for(int j = 0; j < 2; j++)
{
Pair _ans;
_ans.x = ans.x * sign[i][0] * node[dept + 1].x + _sign[j][0] * 3 * ans.y * sign[i][1] * node[dept + 1].y;
_ans.y = ans.x * sign[i][1] * node[dept + 1].y + _sign[j][1] * ans.y * sign[i][0] * node[dept + 1].x;
if(Mem.find(_ans) != Mem.end()) return;
Mem.insert(_ans);
dfs(dept + 1, cnt, _ans);
}
}
}
void Merge(Pair node[], int cnt)
{
Pair ans;
for(int i = 0; i < 4; i++)
{
ans.x = sign[i][0] * node[0].x;
ans.y = sign[i][1] * node[0].y;
Mem.insert(ans);
dfs(0, cnt, ans);
}
}
void Filter(LL B)
{
set<Pair>::iterator it;
for(it = Set.begin(); it != Set.end(); it++)
{
LL a = it->x - it->y;
if(a & 1) continue;
a >>= 1;
LL b = it->y;
LL c = -a - b;
LL _x = B + a - c;
if(_x % 3) continue;
_x /= 3;
LL _y = _x - a;
LL _z = _x + c;
if(_x > _z) swap(_x, _z);
if(_y > _z) swap(_y, _z);
if(_x > _y) swap(_x, _y);
Res res;
res.x = _x;
res.y = _y;
res.z = _z;
_Set.insert(res);
}
set<Res>::iterator _it;
for(_it = _Set.begin(); _it != _Set.end(); _it++)
printf("%lld %lld %lld\n", _it->x, _it->y, _it->z);
}
void Response(LL a[], int cnt)
{
LL A = a[0];
LL B = a[1];
LL n = 3 * A - B * B;
if(n == 0 && B % 3 == 0)
{
printf("%lld %lld %lld\n", B / 3, B / 3, B / 3);
return;
}
if(n < 2) return;
a += 2;
cnt -= 2;
sort(a, a + cnt);
for(int i = 0; i < cnt; i++)
{
while(n % a[i] == 0)
{
vec.push_back(a[i]);
n /= a[i];
}
}
cnt = 0;
vector<LL>::iterator it;
for(it = vec.begin(); it != vec.end(); it++)
a[cnt++] = *it;
for(int i = cnt; i >= 1; i--)
a[i] = a[i-1];
a[0] = 2;
cnt++;
if(!getData(node, a, cnt)) return;
Merge(node, cnt);
Filter(B);
}
int main()
{
int T;
scanf("%d", &T);
getchar();
for(int t = 1; t <= T; t++)
{
vec.clear();
Mem.clear();
Set.clear();
_Set.clear();
int cnt;
gets(str);
Prepare(str, a, cnt);
printf("Case #%d:\n", t);
Response(a, cnt);
}
return 0;
}
最后附上鸟神的思路,虽然我不懂,但我感觉好厉害!!!