HDU 3231 Box Relations（拓扑排序）

题目链接：Click here~~

题意：

在三维空间内，有n个长方体，棱都与坐标轴平行。给出一些关系，问是否可能，若可能，输出其中的一种。

关系有两种：

1、某两个长方体相交。

2、某个长方体的所有点的某一维的坐标完全小于另一个长方体的任意一点。

解题思路：

首先，对于棱与坐标轴平行的长方体，在某一维中，它里面的点可以看做包含在长方体的两个平面内，且点的坐标正好在两个平面的坐标的区间内。

而题目让我们所求的，正是坐标区间，于是我们可以求平面的坐标来得到。

然后，考虑相交的情况，我们可以得出：若某两个长方体相交，当且仅当每一维中，其中的一个长方体的面插进了另一个长方体的内部。

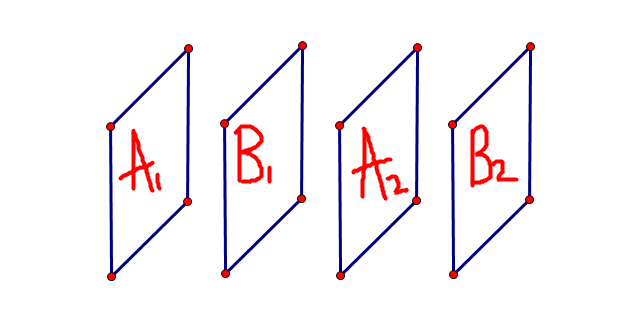
我们以 y 轴为例，画出上图，题中的信息只给出了A和B相交，但是我们不知道谁是A，谁是B，

所以我们只能得到一些与A、B无关的关系：A1<B2、B1<A2，即一个长方体的左面一定小于另一个长方体的右面。

于是我们可以根据这些偏序关系，把长方体的6个面抽象成6个点，对三维分别作拓扑排序，其中每一维只与2个面有关。

#include <queue>
#include <stdio.h>
#include <string.h>
using namespace std;
#define N 2005

struct T
{
    int v,next;
}E[3][N*100];

struct TT
{
    int head,rd,dep;
}V[3][N];

int top[3],ans,n,m;

void Add_Edge(int k,int u,int v)
{
    E[k][top[k]].v = v;
    E[k][top[k]].next = V[k][u].head;
    V[k][u].head = top[k]++;
    ++V[k][v].rd;
}

bool Top_Sort(int k)
{
    queue<int> Q;
    for(int i=1;i<=n;i++)
        if(V[k][i].rd == 0)
            Q.push(i);
    int cnt = 0;
    while(!Q.empty())
    {
        ++cnt;
        int p = Q.front();
        for(int i=V[k][p].head;i!=NULL;i=E[k][i].next)
        {
            int q = E[k][i].v;
            --V[k][q].rd;
            if(V[k][q].rd == 0)
            {
                Q.push(q);
                V[k][q].dep = V[k][p].dep + 1;
            }
        }
        Q.pop();
    }
    return cnt == n;
}
int main()
{
    int u,v,nn,ncase=0;
    char cmd;
    while(~scanf("%d%d%*c",&nn,&m),nn)
    {
        memset(V,0,sizeof(V));
        top[0] = top[1] = top[2] = 1;
        n = 2*nn;
        for(int k=0;k<3;k++)
            for(int i=1;i<=nn;i++)
                Add_Edge(k,i,i+nn);
        while(m--)
        {
            scanf("%c%d%d%*c",&cmd,&u,&v);
            if(cmd == 'I')
            {
                for(int k=0;k<3;k++)
                {
                    Add_Edge(k,u,v+nn);
                    Add_Edge(k,v,u+nn);
                }
            }
            else
                Add_Edge(cmd-'X',u+nn,v);
        }
        printf("Case %d: ",++ncase);
        if(!Top_Sort(0) || !Top_Sort(1) || !Top_Sort(2))
            puts("IMPOSSIBLE\n");
        else
        {
            puts("POSSIBLE");
            for(int i=1;i<=nn;i++)
                printf("%d %d %d %d %d %d\n",V[0][i].dep,V[1][i].dep,V[2][i].dep,V[0][i+nn].dep,V[1][i+nn].dep,V[2][i+nn].dep);
            puts("");
        }
    }
    return 0;
}