循环与递归
循环
(1)对于任意n矩阵输出如下规律图形
1
5 28 6 3
10 9 7 4
void fun(){
int i,j;
int n,k;
int a[100][100];
cout<<"请输入n: ";
cin>>n;
k=0;
for(i=0;i<n;i++){
for(j=0;j<n-i;j++){
k++;
a[i+j][j] = k;
}
}
for(i=0;i<n;i++){
for(j=0;j<=i;j++)
cout<<a[i][j]<<"\t";
cout<<endl<<endl;
}
}
(2)输出1000以内所有完数
完数:一个数恰好等于它所有因子之和
如 6 = 1+2+3 (1,2,3都是6的因子)
void main(){
int i,j;
int sum,k=0;
int a[30];
for(i=0;i<1000;i++){
sum = 1;
for(j=2;j<=i/2;j++)
if(i%j==0)
sum += j;
if(i == sum)
a[k++] = i;
}
cout<<"完数有:"<<endl;
for(i=0;i<k;i++)
cout<<a[i]<<" ";
}
完数有:
1 6 28 496
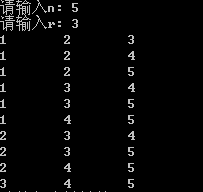
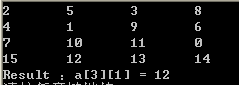
(3)求一个矩阵的鞍点,即在行上最小列上最大的点
//求鞍点
void fun(int a[][4],int n){
int i,j;
int min,minNum;
for(i=0;i<n;i++){
min = a[i][0];
minNum = 0;
for(j=0;j<n;j++)
if(a[i][j]<min){
min = a[i][j];
minNum = j;
}
//cout<<"min"<<i<<": "<<min<<endl;
bool b = true;
for(j=0;j<n;j++)
if(min<a[j][minNum])
b = false;
if(b)
cout<<"Result :a["<<i<<"]["<<minNum<<"] = "<<min<<endl;
}
}
递归
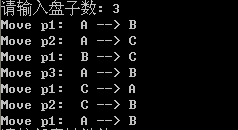
(1)汉诺塔
void hanoi(int n,char a,char b,char c){
if(n>0)
{
hanoi(n-1,a,c,b);
cout<<"Move p"<<n<<": "<<a<<" --> "<<b<<endl;
hanoi(n-1,c,b,a);
}
}
(2)整数划分
将n表示成一系列正整数之和的表达式
如 6 可划分为:
6
5+1
4+2 4+1+1
3+3 3+2+1 3+1+1+1
2+2+2 2+2+1+12+1+1+1+1
1+1+1+1+1+1
//整数划分
int divi(int n,int m){
if(n<0)
cout<<"cin Error"<<endl;
else if(n<=1||m==1)
return 1;
else if(n<m)
return divi(n,n);
else
return divi(n,m-1) + divi(n-m,m);
}
(3)//任何数都可以用2的r次幂来表示
7 = 2^2 + 2^1 + 2^0
1315 = 2^10 + 2^8 + 2^5 + 2^1 +2^0
//任何数都可以用2的r次幂来表示
void tryR(int n,int r){
if(n==1)
cout<<"2^"<<r;
else{
tryR(n/2,r+1);
if(n%2==1)
cout<<" + 2^"<<r;
}
}
循环与递归比较
n个自然数中r个数的组合排序(不考虑相同数)