快速排序
欢迎Java爱好者品读其他算法详解:
简单比较排序:http://blog.csdn.net/ysjian_pingcx/article/details/8652091
冒泡排序: http://blog.csdn.net/ysjian_pingcx/article/details/8653732
选择排序: http://blog.csdn.net/ysjian_pingcx/article/details/8656048
直接插入排序:http://blog.csdn.net/ysjian_pingcx/article/details/8674454
快速排序优化:http://blog.csdn.net/ysjian_pingcx/article/details/8687444
快速排序算法<详解>
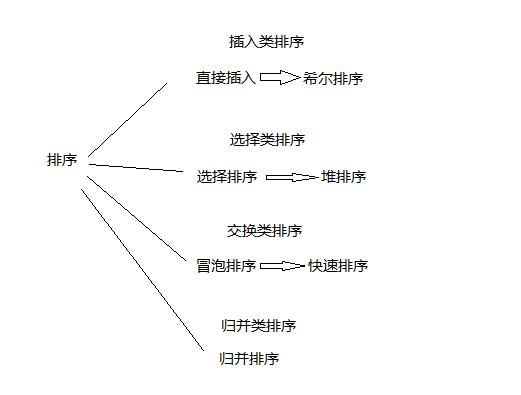
之前介绍的集中排序算法都属于低级的排序算法,在1959年之前,算法家门都没有突破O(n²),直到D.L.Shell在1959年提出了一种排序算法,使得算法界突破了围墙,将算法的时间复杂度有所提升,那么从那以后,算法就大范围的改进,可以说前面的几种低级排序算法都有人发明了进化版的算法,具体如下:
(可以不看本段)今天想写写快速排序,说到快速排序,真是颇有瓜葛啊,有一次去西工大的校园招聘会专场,赶去发现一堆人都挤在宣讲室里面,竞争压力一看便知,但并没有害怕,反而感觉到刺激了,宣讲会算是没有办法挤进去了,因为我是提前到场的,结果在教师外都站了很多人索性找了个凳子坐着,等到笔试,发现好几道算法题,晕乎,前不久刚看过数据结构和算法的题,有点印象,也知道快速排序算法的思路,可是就是没有很清楚的写出来,结果写了个优化的冒泡排序,后来也收到的面试通知,当然Offer也给了,整个笔试题也做的不错,还有校园招聘感觉就是坑爹,基本上没问什么很深的技术,笔试题做好了,就差不多了,给大家分享一下~
快速排序:
这个名字叫的很霸道,快速,不是胡吹的,首先它的时间复杂度O(nlogn),当然时间上交大幅度的优化,实现起来就较低级排序算法要复杂,后面将讲到,使用了递归调用,所以实现起来比较复杂点,但核心思想理解起来很容易的。
核心思想:通过一趟排序将记录分割成独立的两部分,其中一部分的关键字均比另一部分的关键字小,然后分别对这两部分的记录继续进行排序,以达到整个序列有序。
菜鸟代码一步步实现:
我喜欢将函数封装起来,这里涉及到递归调用,且调用的参数列表不一样,通常我们希望给用户提供一个排序的接口,这个接口只接受一个数组,这里用了可变参数:
快速排序的公共接口:
/**
* 快速排序的入口
* @param array
*/
public void quickSort(int... array){
quickSort(0, array.length - 1, array);
}
@这个方法是我个人提取出来的公共接口,也可以不这么设计,然后里面调用的quickSort(0, array.length - 1, array);是用到递归的方法:
递归调用:
/**
* 快速排序的递归调用
* @param low
* @param high
* @param array
*/
private void quickSort(int low, int high, int... array) {
if (low < high) {
int pivot = partition(low, high, array); // 找到枢轴记录的下标
quickSort(low, pivot - 1, array); // 对低子表进行递归排序
quickSort(pivot + 1, high, array); // 对高子表进行递归排序
}
}
@int pivot = partition(low, high, array)这个参数是快速排序算法中核心方法的返回值,就是需找一个枢轴的值,再以这个枢轴为分界线,一分为二,进行递归调用
快速排序的核心程序:
/**
* 快速排序的核心程序
* @param low
* @param high
* @param array
* @return 返回枢轴记录
*/
private int partition(int low, int high, int... array) {
int pivotKey = array[low]; // 将数组的第一个元素作为枢轴记录
while (low < high) {
while (low < high && array[high] >= pivotKey) {
high--;
}
swap(low, high, array);// 把比枢轴记录小的值交换到低端
while (low < high && array[low] <= pivotKey) {
low++;
}
swap(low, high, array);// 把比枢轴记录大的值交换到高端
}
return low; //返回枢轴记录的下标
}
@int povitKey = array[low], 这种方式,是将一个待排序的部分的第一个记录作为一个默认的参照
@外部循环很好理解,就是low的值要小于high的值才能进去;
@这两个循环表示从两端开始进行比较:
while (low < high && array[high] >= pivotKey) {
high--;
}
swap(low, high, array);// 把比枢轴记录小的值交换到低端
while (low < high && array[low] <= pivotKey) {
low++;
}
swap(low, high, array);// 把比枢轴记录大的值交换到高端
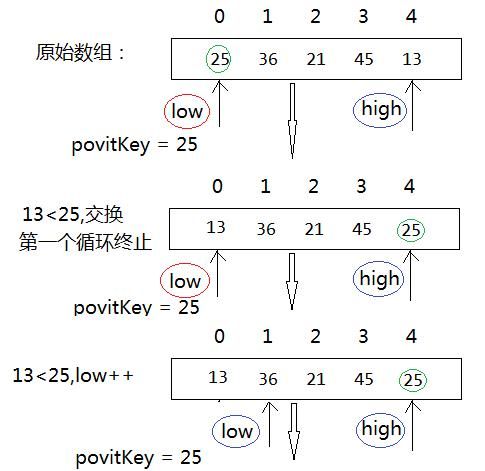
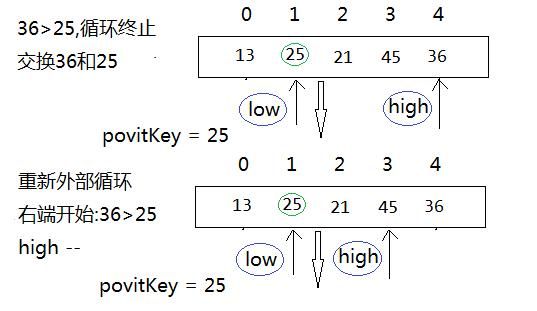
@第一个循环:while (low < high && array[high] >= pivotKey) {high--;},从右端开始,如果array[high] >= pivotKey,指针直接往前走,当有比参照povitKey小的值时,就终止循环,并交换这个小的值和参照的值;
@第二个循环:while (low < high && array[low] <= pivotKey) {low++;},从左端开始,如果array[high] <= pivotKey,指针直接往后面走,当有比povitKey大的值时,就终止循环,并交换这个大的值和参照的值;
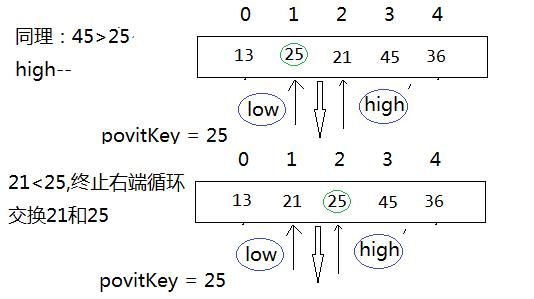
那么这块可以说是快速排序的精髓所在了,下面是一趟排序的过程:
@一趟排序后,将序列分成两个部分,左边部分的记录均小于右边部分的记录,然后用同样的方法分别对两端的记录进行排序。
其实快速排序算法的原理不难,难在发现这种思路,小结一下:
时间复杂度:
最好情况:复杂度为O(nlogn);
最坏情况:比较次数为:n(n - 1) / 2,复杂度为O(n²);
空间复杂度:
函数的递归调用使用的是栈空间,这种排序的算法可以看成是一颗递归树(二叉排序树),最好的情况递归树深度为log2n,空间复杂度为:O(logn);最坏的情况下要进行 (n - 1)次递归调用,空间复杂度为O(n)
平均情况下:空间复杂度为O(logn)
附上完整代码:
/**
* 原始的快速排序法
* @author PingCX
*
*/
public class QuickSort {
public static void main(String[] args) {
QuickSort qComplete = new QuickSort();
int[] array = { 25, 36, 21, 45, 13};
System.out.println(Arrays.toString(array));
qComplete.quickSort(array);//调用快速排序的方法
System.out.println(Arrays.toString(array));//打印排序后的数组元素
}
/**
* 快速排序的入口
* @param array
*/
public void quickSort(int... array){
quickSort(0, array.length - 1, array);
}
/**
* 快速排序的递归调用
* @param low
* @param high
* @param array
*/
private void quickSort(int low, int high, int... array) {
if (low < high) {
int pivot = partition(low, high, array); // 找到枢轴记录的下标
quickSort(low, pivot - 1, array); // 对低子表进行递归排序
quickSort(pivot + 1, high, array); // 对高子表进行递归排序
}
}
/**
* 快速排序的核心程序
* @param low
* @param high
* @param array
* @return 返回枢轴记录
*/
private int partition(int low, int high, int... array) {
int pivotKey = array[low]; // 将数组的第一个元素作为枢轴记录
while (low < high) {
while (low < high && array[high] >= pivotKey) {
high--;
}
swap(low, high, array);// 把比枢轴记录小的值交换到低端
while (low < high && array[low] <= pivotKey) {
low++;
}
swap(low, high, array);// 把比枢轴记录大的值交换到高端
}
return low; //返回枢轴记录的下标
}
/**
* 内部实现,用于交换数组的两个引用值
*
* @param beforeIndex
* @param afterIndex
* @param arr
*/
private void swap(int oneIndex, int anotherIndex, int[] array) {
int temp = array[oneIndex];
array[oneIndex] = array[anotherIndex];
array[anotherIndex] = temp;
}
}
下面是面向对象语言中可比较类型的快速排序:
/**
* 任意可以比较的类型的快速排序法
* @author PingCX
*
*/
public class QuickSortT {
public static void main(String[] args) {
QuickSortT qComplete = new QuickSortT();
//Integer实现了Comparable接口
Integer[] array = { 25, 36, 21, 45, 13};
System.out.println(Arrays.toString(array));
qComplete.quickSort(array); // 调用快速排序的方法,参数必须是实现Comparable接口
System.out.println(Arrays.toString(array)); // 打印排序后的数组元素
}
/**
* 快速排序的入口
*
* @param array
*/
public <T extends Comparable<T>> void quickSort(T[] array) {
quickSort(0, array.length - 1, array);
}
/**
* 快速排序的递归调用
*
* @param low
* @param high
* @param array
*/
private <T extends Comparable<T>> void quickSort(int low, int high,
T[] array) {
if (low < high) {
int pivot = partition(low, high, array); // 找到枢轴记录的下标
quickSort(low, pivot - 1, array); // 对低子表进行递归排序
quickSort(pivot + 1, high, array); // 对高子表进行递归排序
}
}
/**
* 快速排序的核心程序
*
* @param low
* @param high
* @param array
* @return 返回枢轴记录
*/
private <T extends Comparable<T>> int partition(int low, int high,
T[] array) {
T pivotKey = array[low]; // 将数组的第一个元素作为枢轴记录
while (low < high) {
while (low < high && array[high].compareTo(pivotKey) >= 0) {
high--;
}
swap(low, high, array);// 把比枢轴记录小的值交换到低端
while (low < high && array[low].compareTo(pivotKey) <= 0) {
low++;
}
swap(low, high, array);// 把比枢轴记录大的值交换到高端
}
return low; // 返回枢轴记录的下标
}
/**
* 内部实现,用于交换数组的两个引用值
*
* @param beforeIndex
* @param afterIndex
* @param arr
*/
private <T extends Comparable<T>> void swap(int oneIndex, int anotherIndex,
T[] array) {
T temp = array[oneIndex];
array[oneIndex] = array[anotherIndex];
array[anotherIndex] = temp;
}
}
欢迎Java爱好者品读其他算法详解:
简单比较排序:http://blog.csdn.net/ysjian_pingcx/article/details/8652091
冒泡排序: http://blog.csdn.net/ysjian_pingcx/article/details/8653732
选择排序: http://blog.csdn.net/ysjian_pingcx/article/details/8656048
直接插入排序:http://blog.csdn.net/ysjian_pingcx/article/details/8674454
快速排序优化:http://blog.csdn.net/ysjian_pingcx/article/details/8687444