KMP算法学习笔记--按定义计算next数组(个人参考)

具体理论，请看《大话数据结构》、《数据结构(C语言版)》严蔚敏。

此文为此算法的补充说明。

1.直接的子串搜索算法

//函数功能:返回子串T在主串S中第一次被发现的位置
//返回值:如果被发现 返回子串首字母在S中的位置 否则返回-1
//注意:子串T和S从索引1开始
int FindFirstPosition(const std::string & S, const std::string & T)
{
	int sLen = S.size()-1;
	int tLen = T.size()-1;
	int i=1; //0
	int j=1; //0
	while(i<=sLen)
	{
		if(j>tLen) 
			return i-j+1;

		if(S[i] == T[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i-j+2; //i退回到上次匹配首位的下一位
			j = 1;		  //j退回到子串T的首位
		}
	}

	return -1;
}

难点主要为这句代码

i = i-j+2; //i退回到上次匹配首位的下一位

看下图

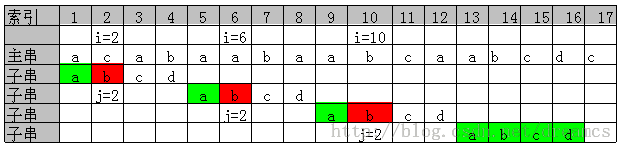
if(S[i] == T[j])之后，第一次S[i] != T[j]时，主串i偏移值为黄色长条长度,子串j偏移值为蓝色长条长度。

子串要再与主串比较，子串的偏移值j自然为0,主串的i则位于橙色格子处。

则橙色格子处的偏移值=黄色长条长度-蓝色长条长度+1=i-j+2=7-3+2=6

2.优化

看如下例子

可归纳出一规则：如果子串中没有重复项，下一次比较位置为按上次刚开始比较位置+子串长度+1。

再使用符号语言描述:设主串为S={A1,A2,...,An},子串为T={a1,a2,...am},主串的比较位置为i,子串的比较为j,

如果T中没有重复项,则匹配失败后,j=i-j+T.length+1

例如上图第一次比较时，i=2,j=2，下一次比较位置 pos=2-2+4+1=5。再下一次比较位置pos=6-2+4+1=9。如下图所示。

如果T中有重复项，应该如何处理?

看此具体例子

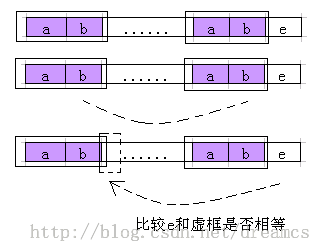
当第一次比较时主串的子串A1A2A3A4A5==子串的子串a1a2a3a4a5,下一次比较时，子串的比较位置j=3。

j=粉色子串长度+1。粉色子串的最大长度=子串的最大相似度。

子串的最大相似度定义:子串为T={a1,a2,...am}

A1, am

A1,a2, ||am-1,am

A1,a2,a3, ||am-2,am-1,am

A1,a2,...ak, //am-k+1,am-k,...am-k-1,...am

j详细公式【2】P81 4-5公式

使用【2】P81 4-5公式求next数组

void CalcNextArrayPrimarily(const std::string & pattern, std::vector<int> & next)
{
	int pLen = pattern.size();
	//字?符?串?索÷引皔从洙?开a始? pattern[0]为a点?位?符? 故ê长¤度è减?1
	pLen--;

	if(pLen>0)//当獭纉=1时骸?next[j]=0;
		next[1] = 0;

	for(int j=2; j<=pLen; j++)
	{
		for(int k=2; k<j;k++)
		{
			std::string::const_iterator ite = pattern.begin()+1; //索÷引皔从洙?开a始?
			std::string pFront(ite, ite+k-1);
			int t = j-k;
			std::string pBack(ite+t, ite+j-1);
			if(pFront == pBack)
			{
				if(k>next[j])
					next[j] = k;
			}
		}
	}
}

3.经典算法

//T[0] 保存字符串的长度
void GetNextArray(char T[], int next[])
{
	//求模式串T的next函数值并存入数组next
	int i=1;
	next[1]=0;
	int j = 0;
	while(i<T[0])
	{
		if(j==0 || T[i]==T[j])
		{
			i++;
			j++;
			next[i] = j;
		}
		else
			j = next[j];
	}
}

设子串T1=a1...a(k-1)与子串T2=aj-k+1...aj-1, j为当前模式串长度。若a(k-1)=a(j-1)，next(j)=next(j)+1,这很好

理解。若a(k-1)!=a(j-1)时，如何处理？看下图

参考文献

【1】《大话数据结构》

【2】《数据结构(C语言版)》严蔚敏。

附：完整源码

#include <string>
#include <iostream>
#include <vector>

//函数功能:返回子串T在主串S中第一次被发现的位置
//返回值:如果被发现 返回子串首字母在S中的位置 否则返回-1
//注意:子串T和S从索引1开始
int FindFirstPosition(const std::string & S, const std::string & T)
{
	int sLen = S.size()-1;
	int tLen = T.size()-1;
	int i=1; //0
	int j=1; //0
	while(i<=sLen)
	{
		if(j>tLen) //因为j递增了一次 所以j == tLen 不然则为j == tLen -1
			return i-j+1;

		if(S[i] == T[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i-j+2; //i退回到上次匹配首位的下一位
			j = 1;		  //j退回到子串T的首位
		}
	}

	return -1;
}


void CalcNextArrayPrimarily(const std::string & pattern, std::vector<int> & next)
{
	int pLen = pattern.size();
	//字符串索引从1开始 pattern[0]为点位符 故长度减1
	pLen--;

	if(pLen>0)//当j=1时 next[j]=0;
		next[1] = 0;

	for(int j=2; j<=pLen; j++)
	{
		for(int k=2; k<j;k++)
		{
			std::string::const_iterator ite = pattern.begin()+1; //索引从1开始
			std::string pFront(ite, ite+k-1);
			int t = j-k;
			std::string pBack(ite+t, ite+j-1);
			if(pFront == pBack)
			{
				if(k>next[j])
					next[j] = k;
			}
		}
	}
}

//T[0] 保存字符串的长度
void GetNextArray(char T[], int next[])
{
	//求模式串T的next函数值并存入数组next
	int i=1;
	next[1]=0;
	int j = 0;
	while(i<T[0])
	{
		if(j==0 || T[i]==T[j])
		{
			i++;
			j++;
			next[i] = j;
		}
		else
			j = next[j];
	}
}

//函数功能:返回子串T在主串S中第一次被发现的位置
//返回值:如果被发现 返回子串首字母在S中的位置 否则返回-1
int KMP(const std::string & S, const std::string & T, int next[])
{
	int sLen = S.size()-1;
	int tLen = T.size()-1;
	int i=1; //0
	int j=1; //0
	while(i<=sLen)
	{
		if(j>tLen) //因为j递增了一次 所以j == tLen 不然则为j == tLen -1
			return i-j+1;

		if(j==0 ||S[i] == T[j]) //j==0 因为j=next[j]时,next[j]可能为0
		{
			i++;
			j++;
		}
		else
		{
			i = i-j+2; //i退回到上次匹配首位的下一位
			//j = 1;		  //j退回到子串T的首位
			j = next[j];
		}
	}

	return -1;
}

void TestNextArray()
{
	///////////////////////////////////////
	std::string S1("*kapibcumbcbfe");
	std::string T1("*bc");
	int index1 =FindFirstPosition(S1, T1);
	std::cout<<index1<<std::endl;

	std::string S2("*kapibcumbcbfe");
	std::string T2("*bcb");
	int index2 =FindFirstPosition(S2, T2);
	std::cout<<index2<<std::endl;
	///////////////////////////////////////////

	std::string pattern("*abaabcac"); //索引从1开始
	std::vector<int> next1(pattern.size(), 1);
	CalcNextArrayPrimarily(pattern, next1);

	std::string pattern2("*akakffakake"); //索引从1开始
	std::vector<int> next2(pattern2.size(), 1);
	CalcNextArrayPrimarily(pattern2, next2);

	char T3[12]={ 11,'a', 'k', 's', 'k', 'f', 'f', 'a', 'k', 'a', 'k','e'};
	int next3[12];
	GetNextArray(T3, next3);
	/////////////////////////////////////////////////////////
	std::string S4("*kapibcumbcbfe");
	std::string T4("*bc");
	std::vector<int> next4(T4.size(), 1);
	CalcNextArrayPrimarily(T4, next4);
	
	std::vector<int> next5(T4.size(), 1);
	char T4_1[3]={2,'b', 'c'};
	GetNextArray(T4_1, next5.data());

	int index4 =KMP(S4, T4, next4.data());
	std::cout<<index4<<std::endl;
	int index5 =KMP(S4, T4, next5.data());
	std::cout<<index4<<std::endl;

	std::string S6("*acabaabaabcacaabc");
	std::string  T6="*abaabcac";
	T6[0]=(char)6;
	char T6_1[9]={8,'a','b','a','a','b','c','a','c'};
	std::vector<int> next6(T6.size(), 1);
	GetNextArray(T6_1, next6.data());
	int index6 =KMP(S6, T6, next6.data());
	std::cout<<index6<<std::endl;

	char T7_1[9]={8,'a','b','c','e','a','b','c','c'};
	std::vector<int> next11(9, 1);
	GetNextArray(T7_1, next11.data());

}