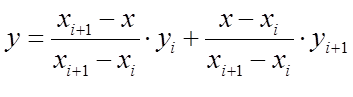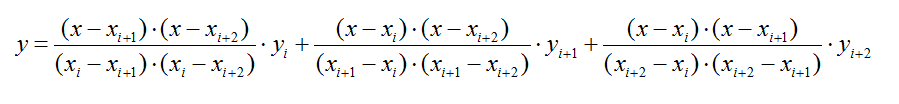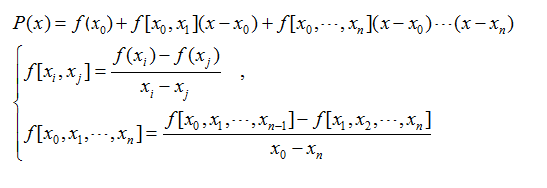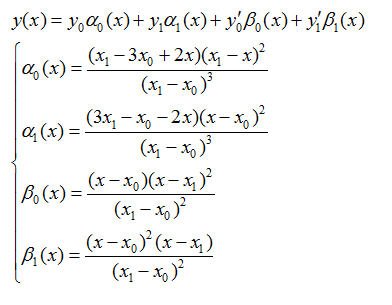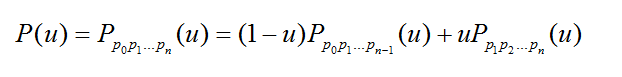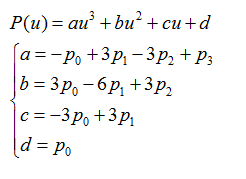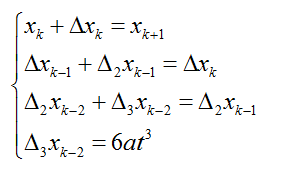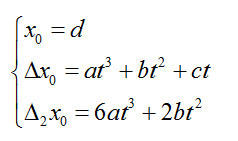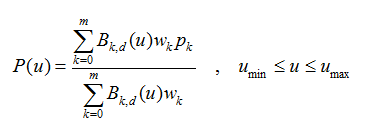常用的插值函数

/*学校的数值分析课程正在讲插值函数，就趁着五一总结一下我所知道的常用的插值函数。每种插值方法都配有图片样例和OpenGL实现代码*/

/*目前由于时间和精力的原因，暂时缺少B-样条和NURBS样条的样例和代码，以后会找时间补上~*/

       据维基百科，科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据，根据这些数据，我们往往希望得到一个连续的函数（也就是曲线）或者更加密集的离散方程与已知数据相吻合，这过程就叫做拟合。通过拟合得到的函数获得未知点的数据的方法，叫做插值。其中，拟合函数经过所有已知点的插值方法，叫做内插。

插值方法

• 多项式插值

        对于大部分多项式插值函数，插值点的高度值可以视为所有（或某些）节点高度值的线性组合，而线性组合的系数一般是x坐标的多项式函数，称作基函数。对于一个节点的基函数，它在x等于该节点的x时等于1，在x等于其他节点的x时等于0。这就保证曲线必定经过所有节点，所以属于内插方法。

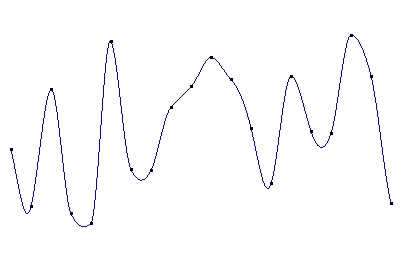
        在本小节，均以一组随机数作为已知的高度值，使它们对应于间隔固定的x坐标，使用不同的插值函数获得各已知点（称为插值函数的节点）之外其它x坐标所对应的高度值，画出这些点所对应的曲线。再把所有高度值转换成灰度值，以颜色的变化比较各插值函数。

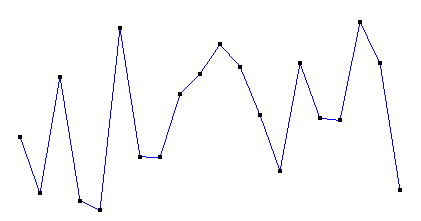
        原点列如图：（假定横向为x，纵向为y。各点x坐标的间隔是固定的，但y坐标是随机的）

     线性插值

        线性插值是用一系列首尾相连的线段依次连接相邻各点，每条线段内的点的高度作为插值获得的高度值。

        以(xi,yi)表示某条线段的前一个端点，(x(i+1),y(i+1))表示该线段的后一个端点，则对于在[xi,x(i+1)]范围内的横坐标为x的点，其高度y为：

       为便于与后面各函数比较，写成比较对称的形式：

        其中，yi和y(i+1)的两个参数称为基函数，二者之和为1，分别代表yi和y(i+1)对插值点高度的权值。

        插值图像如下：

        将高度转化为灰度，得到如下条带：

        线性插值的特点是计算简便，但光滑性很差。如果用线性插值拟合一条光滑曲线，对每一段线段，原曲线在该段内二阶导数绝对值的最大值越大，拟合的误差越大。

     二次插值

       如果按照线性插值的形式，以每3个相邻点做插值，就得到了二次插值：

        实现代码如下：

void quadratic(float p[20][2])
{
	float x,y;
	int i;
	float x01,x02,x12;

	glColor3f(0.0,0.0,1.0);
	glBegin(GL_LINE_STRIP);
	for(i=0;i<20;i+=2)
	{
		x01=p[i][0]-p[i+1][0];
		x02=p[i][0]-p[i+2][0];
		x12=p[i+1][0]-p[i+2][0];
		
		for(x=p[i][0];x<=p[i+2][0];x+=1.0)
		{
			y=(x-p[i+1][0])*(x-p[i+2][0])/x01/x02*p[i][1]-(x-p[i][0])*(x-p[i+2][0])/x01/x12*p[i+1][1]+(x-p[i][0])*(x-p[i+1][0])/x02/x12*p[i+2][1];
			glVertex2f(x,y);
		}
	}
	glEnd();
}

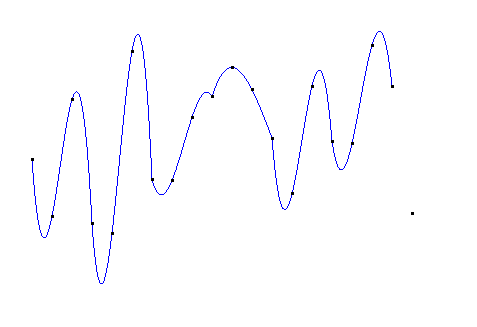
        二次（分段）插值图像如下：

        转换成灰度值如图：

        二次插值在每段二次曲线内是光滑的，但在每条曲线的连接处其光滑性可能甚至比线性插值还差。二次插值只适合3个节点的情形，当节点数超过3个时，就需要分段插值了。

     Cubic插值

       如果想要保证各段曲线连接处光滑（一阶导数相同），并且不想使用除法运算，可以考虑Cubic插值函数：

        其中，v代表插值点，v0、v1、v2、v3代表4个连续的节点。t取值为[0,1]，将会产生一段连接v1和v2的曲线。也就是说，如果有n个节点，Cubic插值函数将会产生(n-2)段曲线，位于首尾两端的节点不会纳入曲线。

        实现代码如下：

float cubic(float v0,float v1,float v2,float v3,float x)
{
	float v32=v3-v2;
	float v01=v0-v1;
	float v20=v2-v0;
	float temp=(v32-v01)*x;
	temp=(temp+v01+v01-v32)*x;
	temp=(temp+v20)*x+v1;
	return temp;
}

void drawCubic(float p[20])
{
	float x,y;
	int step;
	float delta;

	glColor3f(0.0,0.0,1.0);
	glBegin(GL_LINE_STRIP);
	for(step=0;step<17;step++)
	{
		for(delta=0.0;delta<=1.0;delta+=0.05)
		{
			x=delta*(p[step+1][0]-p[step][0])+p[step][0];
			y=cubic(p[step],p[step+1],p[step+2],p[step+3],delta);
			glVertex2f(x,y);
		}
	}
	glEnd();
}

        Cuibc插值图像如下：

        转化成灰度如图：

        Cubic插值可以产生整体上光滑的曲线，但容易产生较剧烈的波动，使得曲线的最高点比最高的节点还高、曲线的最低点比最低的节点还低。所以对颜色等取值有严格的上下界的数据进行插值时，会造成曲线的截取，破坏其光滑性。比如颜色（RGB三个分量取值范围都是[0,255]），如果最高的节点是255，最低的节点是0，那么插值后负数会被截取成0，大于255的数会被截取成255。

    拉格朗日多项式插值

        依照线性插值和二次插值的思路，可以增加基函数分子和分母的阶数，构造拉格朗日插值多项式：

        一个n次的拉格朗日插值函数可以绘制经过(n+1)个节点的曲线，但运算量非常大。而且在次数比较高时，容易产生剧烈的震荡（龙格现象）。所以要选择位置特殊的节点（比如切比雪夫多项式的零点）进行插值，或使用多个次数较低的拉格朗日函数分段插值。（关于拉格朗日多项式和龙格现象，详见维基百科链接）

        分段插值实现代码如下：

//n为次数，nmax为节点的总数。n不大于nmax
void lagrange(float p[][2],int n,int nmax)
{
	float x,y;
	int i,j,t;
	float temp;

	glColor3f(0.0,0.0,1.0);
	for(i=0;i<=(nmax-1);i+=(n-1))
	{
		glBegin(GL_LINE_STRIP);
		for(x=p[i][0];x<=p[i+n-1][0];x+=1.0)
		{
			y=0.0;
			for(j=0;j<n;j++)
			{
				temp=1.0;
				for(t=0;t<n;t++)
				{
					if(t==j)
						continue;
					temp*=(x-p[i+t][0])/(p[i+j][0]-p[i+t][0]);
				}
				y+=temp*p[i+j][1];
			}
			glVertex2f(x,y);
		}
		glEnd();
	}
}

        使用4次拉格朗日多项式分段插值：

        转化为灰度：

        拉格朗日多项式插值也存在连接处不光滑的问题。

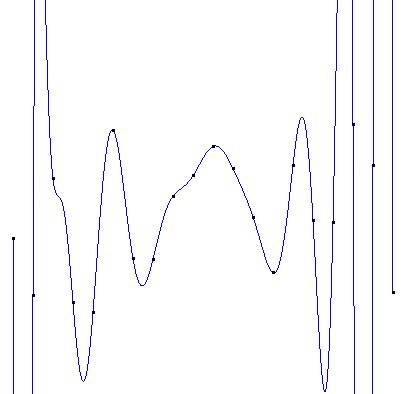
        如果直接使用20次的拉格朗日插值，得到的图像如下：

        这样的插值曲线显然是不能容忍的~

     牛顿插值

        拉格朗日插值每增加一个节点，整个函数要重新计算，计算量巨大。而牛顿插值每增加一个点只需要在多项式的最后增加一项，而且各基函数的系数可以递归计算，减少了很多计算量。

        实现代码如下：

void newton(float p[][2],int n,int nmax)  
{  
    float x,y;  
    int i,j,t;  
    float temp;  
    float f[20][20];  
  
    glColor3f(0.0,0.0,1.0);  
    for(i=0;i<=(nmax-1);i+=(n-1))  
    {  
        for(t=0;t<n;t++)  
        {  
            f[t][0]=(p[i+t][1]-p[i+t+1][1])/(p[i+t][0]-p[i+t+1][0]);  
            for(j=1;j<=t;j++)  
				f[t][j]=(f[t-1][j-1]-f[t][j-1])/(p[i+t-j][0]-p[i+t+1][0]);  
        }  
  
        glBegin(GL_LINE_STRIP);  
        for(x=p[i][0];x<=p[i+n-1][0];x+=1.0)  
        {  
            y=p[i][1];  
            temp=1.0;  
            for(j=0;j<n;j++)  
            {  
                temp*=x-p[i+j][0];  
                y+=temp*f[j][j];  
            }  
            glVertex2f(x,y);  
        }  
        glEnd();  
    }  
}  

        可能由于计算精度的原因，牛顿插值绘制的曲线与拉格朗日插值的曲线略有不同。但次数较高时，牛顿插值也会产生剧烈的震荡。分段4次牛顿插值图像如下：

        转化成灰度如下：

        牛顿插值也存在连接处不光滑的缺陷。

    埃尔米特插值

        以上各多项式插值方法的插值条件都是各节点的坐标，在以低阶函数分段插值时虽然可以保持曲线的稳定（比较平缓），但在各分段曲线的连接处无法保持光滑（一阶导数相等）。埃尔米特插值方法不但规定了各节点的坐标值，还规定了曲线在每个节点的各阶导数，这样就可以既保持曲线的稳定，又保证在连接处足够光滑。

        以3次二重（"m重"就是规定坐标和曲线在所有节点处1到m-1阶导数的值）埃尔米特插值为例：

        4个基函数满足分别只在y0，y1，y0的导数，y1的导数处等于1，而在其他3个条件下等于0。可以把埃尔米特插值看作对坐标和导数的插值的组合。

        曲线在每个节点的导数可以根据相邻节点和它的相对位置确定，也可以完全随机生成。只要位置比较高和比较低的节点的导数绝对值不是很大，就可以使整条曲线落在最高与最低节点定义的带状区域内，这样就可以避免对插值的截取。

        对于本节的示例节点，一种可能的导数值如下：

grad[20]={-4.0,4.0,0.5,-2.0,1.0,-2.0,-2.0,2.0,1.0,1.0,0.0,-1.0,-4.0,3.0,0.0,-3.0,3.0,0.0,-4.0,-4.0};

        实现代码如下：

//p[i][0],p[i][1]为点i的坐标，p[i][2]为曲线在点i的导数
//nmax为节点的总数
void hermite(float p[][3],int nmax)
{
	float x,y;
	float a1,a0,b1,b0;
	float x00,x11;
	int i;
	float temp;

	glColor3f(0.0,0.0,1.0);
	for(i=0;i<nmax;i++)
	{
		glBegin(GL_LINE_STRIP);
		x00=p[i][0];
		x11=p[i+1][0];
		for(x=p[i][0];x<=p[i+1][0];x+=1.0)
		{
			temp=(x11-x00)*(x11-x00);
			a0=(x11-3*x00+2*x)*(x11-x)*(x11-x)/temp/(x11-x00);
			a1=(-x00+3*x11-2*x)*(x-x00)*(x-x00)/temp/(x11-x00);
			b0=(x-x00)*(x-x11)*(x-x11)/temp;
			b1=(x-x00)*(x-x00)*(x-x11)/temp;
			y=a0*p[i][1]+a1*p[i+1][1]+b0*p[i][2]+b1*p[i+1][2];
			glVertex2f(x,y);
		}
		glEnd();
	}
}

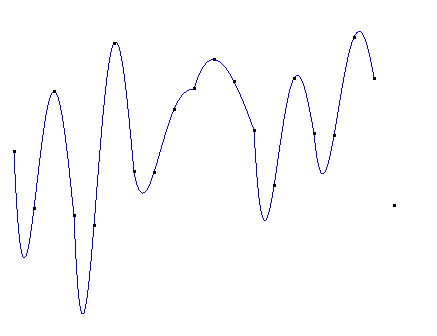
        分段3次埃尔米特插值图像如下：

        转化为灰度如下：

        可见虽然n节点的埃尔米特插值是由(n-1)段曲线构成，但在每一个连接处都是光滑的。

• 样条插值

       B-样条

        B-样条是Bezier样条的一般化，也可推广为NURBS样条。先来介绍一下B-样条：

        该式定义了一个n次的B-样条，它有(m+1)个控制点（样条曲线的“节点”称作控制点，因为这些点控制曲线的弯曲方向和程度，但曲线不一定经过这些点），也就有(m+1)个基函数。一般绘制的是完整的曲线，u(min)取0，u(max)取1。当u取值均匀时，该样条称作均匀B-样条。当m=n时，B-样条退化为Bezier样条。

        函数绘制的曲线始终落在其控制点的凸包（包含一个点集所有点的凸多边形，而且该凸多边形所有顶点都来自这个点集）中。对于一个n次的B-样条，改变一个控制点的位置，只改变它所在的n段曲线（由n+1个控制点定义，且以该点起始）的形状，而不对其余的(m-n)段曲线产生影响。

       Bezier样条

     Bezier（贝塞尔）样条是法国工程师皮埃尔·贝塞尔（Pierre Bézier）在1962年为了设计汽车主体外形曲线而提出的。其一般式表达式为：

        其中，u取值为[0,1]，pk(k=0,...,n)为(n+1)个节点，n称为阶数。

        Bezier样条还可以递归定义为：

        含义是n阶Bezier样条是两条(n-1)阶Bezier样条的插值。

        当阶数降为1时，Bezier插值退化成线性插值。改变任意一个控制点的位置，整条曲线的形状都会发生变化。

        比较常用的Bezier样条是3次Bezier：

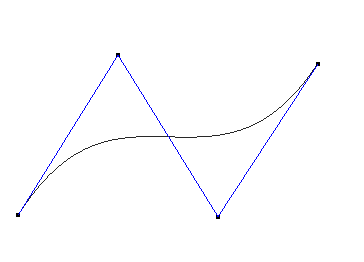
        Beizer样条在首尾端的切线是前两个点和最后两个点的连线。除了第一个点和最后一个点，其他控制点一般都不在曲线上。

        3阶（4控制点）的Bezier函数图像如下：（黑色曲线为Bezier曲线，蓝色折线为控制点的连线）

        Bezier样条可以实现非常快速的运算。为了方便说明，将3次Bezier样条表示成如下形式：

        对于任意给定的u，可以通过合并的方式将原来的7次乘法、4次加法减少为3次乘法、3次加法：

        一般情况下，应用Bezier样条绘制曲线时，都是先给定一个很小的步长t（步长足够小才能保证Bezier曲线的精确），让t从0取到1，从头到尾绘制整条曲线。在t不变的条件下，可以使用更快速的差分方法，利用前一个点计算出下一个点的值，将每步的计算量减小到只有3次加法：

        只需要在绘制曲线之前计算4个常数，就可以很快地计算出曲线上的所有点：

        采用这种方式，Bezier样条的运算量只随阶数线性增长。

        实现代码如下：

void bezier3(float xx0,float yy0,float xx1,float yy1,float xx2,float yy2,float xx3,float yy3)
{
	GLint i;
	GLfloat x,y;
	GLdouble ax,bx,cx,ay,by,cy;
	GLdouble t;
	GLdouble dx,d2x,dy,d2y,delta;
	GLdouble d3x,d3y;

	ax=-xx0+3.0*xx1-3.0*xx2+xx3;
	bx=3.0*xx0-6.0*xx1+3.0*xx2;
	cx=-3.0*xx0+3.0*xx1;
	ay=-yy0+3.0*yy1-3.0*yy2+yy3;
	by=3.0*yy0-6.0*yy1+3.0*yy2;
	cy=-3.0*yy0+3.0*yy1;

	delta=0.0005;
	d3x=6.0*ax*delta*delta*delta;
	d3y=6.0*ay*delta*delta*delta;
	x=xx0;
	y=yy0;

	glBegin(GL_LINE_STRIP);
	glVertex2f(x,y+200);
	d2x=6.0*ax*delta*delta*delta+2.0*bx*delta*delta;
	dx=ax*delta*delta*delta+bx*delta*delta+cx*delta;
	d2y=6.0*ay*delta*delta*delta+2.0*by*delta*delta;
	dy=ay*delta*delta*delta+by*delta*delta+cy*delta;
	for(t=0.0;t<=1.0;t+=delta)
	{
		d2x+=d3x;
		dx+=d2x;
		x+=(float)dx;
		d2y+=d3y;
		dy+=d2y;
		y+=(float)dy;
		glVertex2f(x,y);
	}
	glEnd();
}

       NURBS样条

        NURBS（Non-Uniform Rational B-Splines 非均匀有理B-样条），是贝塞尔样条的推广。“非均匀”的意思是控制点的间隔可以是不均匀的，“有理”的意思是各控制点带有不同的权值。和Bezier样条相比，它对曲线形状的控制更自由：

        其基函数B(k,d)与B-样条的基函数相同，w(k)为各点的权因子。和B-样条一样，改变一个控制点的位置，只改变它所在的n段曲线的形状，而不对其余的(m-n)段曲线产生影响。

插值的一些应用

    噪声

        噪声图像一般需要二维或三维插值函数，不过了解了各一维插值函数，就很容易扩展到二维和三维了。

        关于二维噪声图像的产生，请参见《二维噪声图像》。

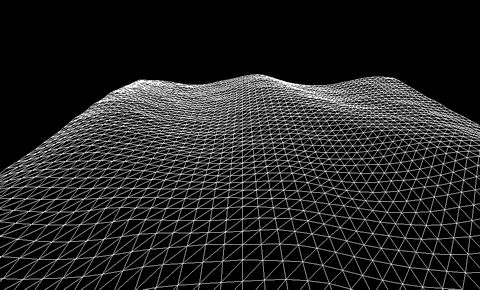
    水波

          下面这个图像就是用插值函数绘制的模拟水波的三维网格（因为动态图片在文章中总是读取失败，所以只能贴张静态图了）：

        虽然这张网格看起来似乎需要二维插值，但这张网格是由6个不同波长和频率的Gestner合成的，每个独立的波形只需要一维插值生成。