KMP算法 Knuth-Morris-Pratt 字符串查找算法

 Knuth-Morris-Pratt 字符串查找算法（常简称为 “KMP算法”）是在一个“主文本字符串”S 内查找一个“词”W 的出现，通过观察发现，在不匹配发生的时候这个词自身包含足够的信息来确定下一个匹配将在哪里开始，以此避免对以前匹配过的字符重新检查。--Wiki定义

这个算法乍看不难，细细考虑起来，却是很难的算法，网上有很多介绍了，我在这里也不重复啰嗦，贴出参考资料，然后给出我自己的例子，程序和分析，以作为这些资料的补充资料。

他们next数组第一个值肯定是-1，我觉得这就不好看，网上的一般都是这种写法，而且基本上都用char实现，大概是标准程序吧，一直都这么写的。

我这里的程序不同的就是我用了string的处理，他们的都是用char的。而且下标处理都和他们的不一样。

我的next数组第一个值也是0.稍微不一样，喜欢的可以研究一下。

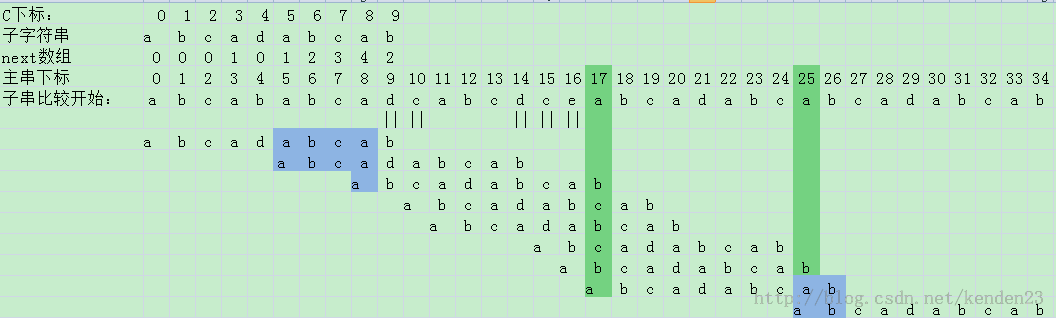
下面是例子示意图：

当前比较值的位置为j，如果当前字符和主字符串不相等，那么就把j位置之前的真后缀和其对应的真前缀重合起来，因为对应的真前缀和真后缀是相等的，那么就不用重新对比一次了，这就是KMP思想的关键所在。
当前比较位置始终保持计算前缀位置+1

可以尝试例子： a b c a d a b c a b 最后一个b是2.这就是回溯到最前面的a，然后比较第二个b得到的数值。 注意：这个是当子串很长的时候才有的情况，当前比较的字符的前一个字符跳到前面相同字符的位子，回溯查找。
思想就是：相同字符往前跳。一定要会举例子，才能明白的！！！

实在不懂的，看下面程序和最后的参考资料。

 其中求next[]数组是运用了动态规划法的思想来求的，其实也可以使用暴力法来求，会简单点。

vector<int> kmpSearch(string &text, string &substr, vector<int> &next)
{
	vector<int> begIndex;
	if(substr.empty() || text.empty()) return begIndex;

	int j = 0;
	for (int i = 0; i < text.size(); i++)
	{
/*当前比较值的位置为j，如果当前字符和主字符串不相等，那么就把j位置之前的真后缀和其对应的真前缀重合起来，因为对应的真前缀和真后缀是相等的，那么就不用重新对比一次了，这就是KMP思想的关键所在。
当前比较位置始终保持计算前缀位置+1
*/
		while (j>0 && substr[j] != text[i])
		{//这里是while不是if，因为不止一个前缀的，如：abcabcdefab;最后的ab前面有两个ab
			j = next[j-1];
		}

		if (substr[j] == text[i])//之前想得不周到，这个判断条件是不能去掉的，因为特殊情况substr只有一个字母的时候，就必须有这个条件
 		{//去掉的话，结果就会不正确！
			j++;
		}

		if (j == substr.size())
		{
			begIndex.push_back(i-j+1);
			j = next[j-1];
		}
	}
	return begIndex;
}

vector<int> generateNext(string &substr)
{
	vector<int> next(substr.size());
	next[0] = 0;
	int j = 0;
	int m = substr.size();
	for (int i = 1; i < m; i++)
	{
/*可以尝试例子： a b c a d a b c a b 最后一个b是2.这就是回溯到最前面的a，然后比较第二个b得到的数值。	注意：这个是当子串很长的时候才有的情况，当前比较的字符的前一个字符跳到前面相同字符的位子，回溯查找。
思想就是：相同字符往前跳。一定要会举例子，才能明白的！！！
*/
		while (j>0 && substr[j] != substr[i])
		{
			j = next[j-1];
		}
		if (substr[j] == substr[i])
 		{
			j++;
		}
		next[i] = j;
	}
	return next;
}
 

int main()
{
	string str1 = "abcababcadcabcdceabcadabcabcadabcab";
	string substr = "abcadabcab";

	cout<<"BF算法结果：\n";
	vector<int> vi = bfSearch(str1, substr);
	for(auto x:vi)
		cout<<x<<" ";
	cout<<endl;

	cout<<"Next数组：\n";
	vector<int> next = generateNext(substr);
	for(auto x:next)
		cout<<x<<" ";
	cout<<endl;

	cout<<"KMP算法结果：\n";
	vector<int> vkmp = kmpSearch(str1, substr, next);
	for(auto x:vkmp)
		cout<<x<<" ";
	cout<<endl;

	system("pause");
	return 0;
}

 

BF算法可以参照下面我的博客：

http://blog.csdn.net/kenden23/article/details/15811425

最后看结果KMP算法和BF算法的结果是一致的。

 

这里是补充资料，入门我就不重复了，看下面的参考资料，不明白可以回来参考参考我的例子：

 比较好懂的英文资料：

http://jakeboxer.com/blog/2009/12/13/the-knuth-morris-pratt-algorithm-in-my-own-words/

 

不过要注意这里的分析和实际写程序的思想又是不大一样的，为什么会这样？因为程序思维和人的思维还是有差别的。

他的分析是为了人好理解，我们写程序是为了计算机好理解。死抱着他的思想去写这个程序的话是写不出来的。

也就是说方法是一样的，但是实际操作起来有点不一样。也正是这么一点不一样，所以光会写伪代码不算多大本事，还是要实际运行处程序才行的。

 

比较好懂的中文资料（差不多就是上面的翻译了）：

http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

Wiki:

http://en.wikipedia.org/wiki/Knuth-Morris-Pratt_algorithm

带程序的博客

http://blog.csdn.net/workformywork/article/details/12780331

http://www.cnblogs.com/dolphin0520/archive/2011/08/24/2151846.html

比较旧的程序但是分析不错的中文博客：

http://www.matrix67.com/blog/archives/115

2014-2-21更新：

重新花了点时间去研究，终于突破了。

其实不难了，更新个自己新写的程序：

//2014-2-21 update
	char *strStr(char *hay, char *ne)
	{
		int len = strlen(hay);
		int n = strlen(ne);
		vector<int> tbl = genTbl(ne, n);
		for (int i = 0, j = 0; i <= len - n; )//改成i<len那么会空串的时候出错
		{
			for ( ; j < len && j < n && hay[i+j] == ne[j]; j++);
			if (j == n) return hay+i;
			if (j > 0) 
			{
				i += j - tbl[j-1] - 1;
				j = tbl[j-1] + 1;
			}
			else i++;
		}
		return nullptr;
	}

	
	vector<int> genTbl(char *ne, int n)
	{
		vector<int> tbl(n, -1);
		for (int i = 1, j = 0; i < n;)
		{
			if (ne[i] == ne[j])
			{
				tbl[i] = j;
				++j;
				++i;
			}
			else if (j > 0) j = tbl[j-1]+1;
			else i++;
		}
		return tbl;
	}

时间效率由原来的暴力法的O(m*n)，优化为O(m+n)；如果两个字符串都很长的时候，优化是十分明显的。