PGM学习之六 从有向无环图（DAG）到贝叶斯网络（Bayesian Networks）

          本文的目的是记录一些在学习贝叶斯网络（Bayesian Networks）过程中遇到的基本问题。主要包括有向无环图（DAG），I-Maps，分解（Factorization），有向分割（d-Separation），最小I-Maps（Minimal I-Maps）等。主要参考Nir Friedman的相关PPT。

1  概率分布（Probability Distributions）

          令X1,...,Xn表示随机变量；令P是X1,...,Xn的联合分布（joint distribution）。如果每个变量均可有两种取值（0-1分布），那么最终我们将得到2^n种取值，也就是说，我们需要用2^n个变量来描述P的分布。

2 随机变量的独立性

       如果随机变量X和Y相互独立（independent），那么：

             1）P（X=x|Y=y）=p(X=x)，对于所有的x和y均成立；2）也就是说，随机变量Y的取值（或者说随机事件Y是否发生），不影响X。

             3）P(X,Y)=P(X|Y)*P(Y)=P(X)*P(Y)；

       推广，如果X1，。。。，Xn独立，那么：

                   P(X1,,,,,Xn)=P(X1)...P(Xn)，共需O(n)个参数。

3 条件独立（Conditional Independence）

        上述独立的情况比较理想，不幸的是，现实中大多数我们感兴趣的随机变量都不是相互独立的。更加常见的假设是条件独立。两个随机变量X和Y对于给定条件Z条件独立，如果：

P(X=x|Y=y,Z=z) = P(X=x|Z=z)，对于所有随机变量取值x,y,z均成立。

也就是说，当我们知道Z的取值时，Y的取值不影响X的预测。记为Ind(X;Y|Z)

4 马尔科夫假设（Markov Assumption）

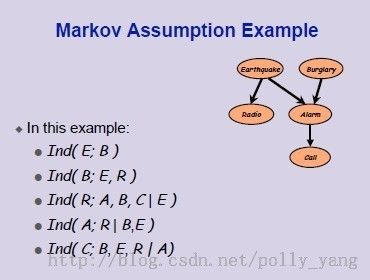
        马尔科夫假设是针对有向无环图做的更清晰的独立性假设。对于图G中的任意一个节点X，X代表一个随机变量，在给定X的父节点集Par(X)的情况下，X和X的所有非子节点相互独立。一般记作Ind(X;NonDesc(x)|Par(x))。这也称作变量的局部马尔科夫性。实例见下图：

                           

5 I-Maps

       一个有向无环图G是分布P的一个I-Map当对G的所有马尔科夫假设也适合于对P（假设G和P均具有相同的随机变量）。这是从有向无环图到概率公式推理的基础。

6 分解 Factorization

        如果G是P的一个I-Map，那么我们能简化P的表示么？

        例如，对于随机变量X和Y，如果Ind(X;Y)，我们可以知道：P(X|Y)=P(X)。

        根据链式法则（Chain Rules），我们知道：P(X,Y)=P(X|Y)*P(Y)=P(X)*P(Y)。

        这样，我们就将P(X,Y)简化成为P(X)*P(Y)的形式。

7 分解定理

       如果G是P的一个I-Map，那么：

8 最小I-Map, Minimal I-Map

一个有向无环图G是P的一个最小I-Map当：G是P的一个I-Map；如果G‘是G的子图，那么G’不是P的I-Map。

9 d-separated 有向分割

d-separated这个概念是由Judea Pearl于1988年提出的算法的名字。这个算法是用来衡量图中的所有的条件独立关系。

令X, Y和Z是一个有向无环图 G中二个不相 交节点的子集，如果在集合X和Y中所有节点间的所有路径都被集合Z所 阻塞，则称集合X和Y被Z集合d-s eparation。

也称Z 为X和Y的切割集。否则，称在给定集合Z下集合X和Y依赖。

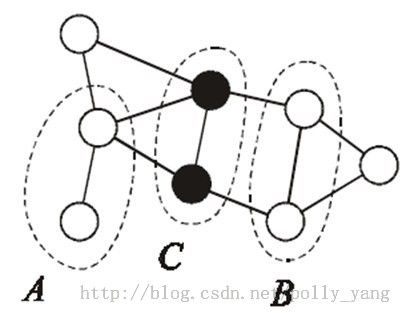
那么，什么时候称点集X和Y中所有节点间的路径被点集Z阻塞呢？如下图所示：

        1.每条从A中的变量（顶点）到B中变量（顶点）的路径都经过集合Z，则称Z分开了点集A和B；

        2.Z阻塞了从A到B的所有路径。

10 信息理论

         增加这个定义的原因是因为评价概率模型时常常要用到，作为笔记留作查阅。

11.扩展阅读

图模型的介绍

An introduction to graphical models，Kevin P. Murphy

关于图模型的课程：课件以书的形式给出，易读

Statistical Learning Theory，berkeley CS281A  

http://www.cs.berkeley.edu/~jordan/courses/281A-fall02/    

更多的tutorials

http://www.cs.ubc.ca/~murphyk/

http://research.microsoft.com/~cmbishop/talks.htm

http://research.microsoft.com/~heckerman/

http://www.autonlab.org/tutorials/

http://www.cs.berkeley.edu/~jordan/tutorials.html

一些工具/源代码

Intel Probabilistic Network Library：C++

www.intel.com/technology/computing/pnl/index.htm 

Jie Cheng ：KDDCup01的优胜者

http://www.cs.ualberta.ca/~jcheng/

Matlab工具：http://prdownloads.sourceforge.net/bnt/