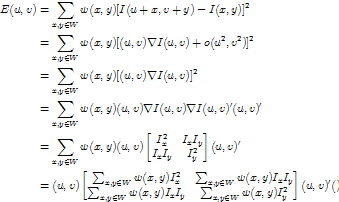Harris原理及OpenCV实
Harris原理及OpenCV实现
概述
Harris算法是一种角点检测算法。
基本思想
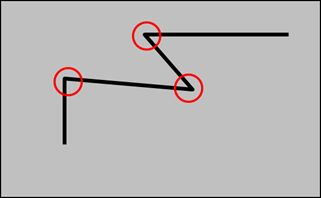
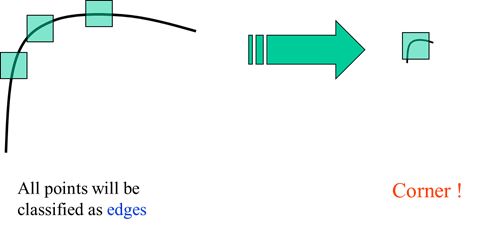
在角点处，绿色小框在图像中沿着任意方向移动，方框覆盖的像素值都会发生很大的改变；平坦区域沿着任意方向都不会有太大变化；边缘区域其实向任意方向移动也不会有什么变化，除非是在边缘的末端。（是不是角点动一动就知道了，是骡子是马拉出来溜溜）
数学描述
表示像素以移动之后像素值变化的方差和：
数学特性
一届泰勒展开：
向指定方向
移动，窗口内的像素值的变化量：
为滤波后的梯度散布矩阵,简写为。
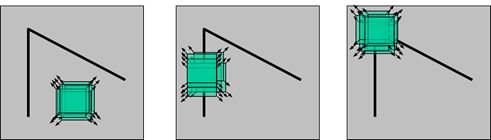
下面用三张图片验证：
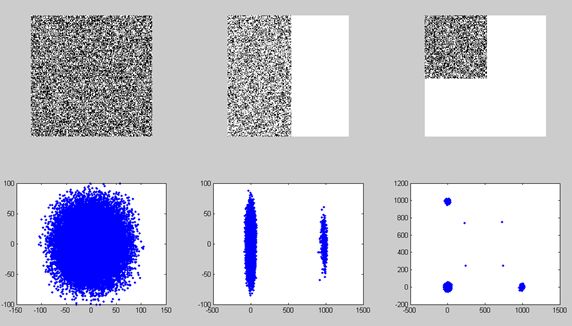
上图是用PS加上5%的杂色，杂色不是很明显，下图第一栏转换成double型后的显示效果，
第二栏是的分布，可以看出，平面的梯度散布范围很小，而边缘则呈扁椭圆，角点呈三角，但可以看到右上角的点
均比较大即我们要找的角点。
对应的特征值如下：
| eigenvalue |
Plane |
Edge |
Corner |
|
|
68483668088 |
116292777117498 |
62741886125931 |
|
|
3358193434 |
7446530637 |
60918946323957 |
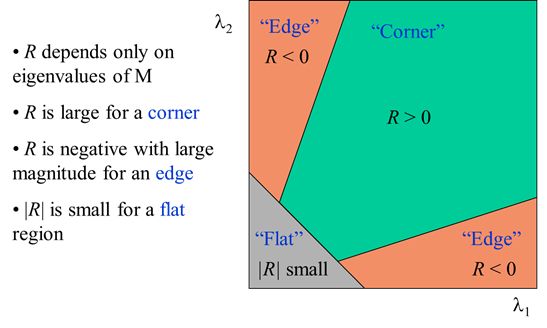
上述只是定性的分析的关系，定量判定如下：
其中经验值
，
越大说明越有可能是角点。
上图为对应的响应。
在SIFT算法中使用了另一种判定方法：
设最大的特征值/最小的特征值为,例如则
考虑下式：
令上式为
，
时为单调递增函数，故
时判断为角点。经验值。为什么角点沿任意方向移动，窗口内的像素都会有很大变化，而平坦区域沿任意方向移动都不会有变化，而边缘沿特定方向移动不会有变化呢？
为什么会有如此特性了，这就取决于M。
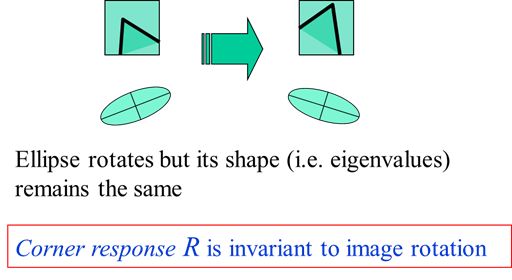
从梯度的散布形状可以判断该点是否是角点。梯度的散布形状又可以由散布矩阵的特征值大小、比例关系反映。因此，对对 进行特征值分解得到特征值 。不变性分析
-
旋转不变性
- 局部仿射不变性
- 尺度不变性-不具备
Harris-Laplace算法具有尺度不变性
算法
- 计算梯度
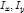，（考虑干扰用Sobel算子滤波），得到三张图片 - 对得到的三张图片继续滤波，实现在窗口
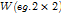下的累积和. - 计算行列式、迹
OpenCV源码分析
cornerEigenValsVecs(constMat&src,Mat&eigenv,intblock_size,
intaperture_size,intop_type,doublek=0.,
intborderType=BORDER_DEFAULT )
{
#ifdef HAVE_TEGRA_OPTIMIZATION
if (tegra::cornerEigenValsVecs(src, eigenv, block_size, aperture_size, op_type, k, borderType))
return;
#endif
int depth =src.depth();
double scale = (double)(1 << ((aperture_size > 0 ?aperture_size : 3) - 1)) *block_size;//1 << 2 *2 =8
if(aperture_size < 0 )
scale *= 2.;
if( depth ==CV_8U )
scale *= 255.;
scale = 1./scale;
CV_Assert(src.type() ==CV_8UC1 ||src.type() ==CV_32FC1 );
Mat Dx, Dy;
if(aperture_size > 0 )
{
//[-1 0 1]
//|-2 0 2|
//[-1 0 1]
Sobel(src, Dx,CV_32F, 1, 0,aperture_size, scale, 0,borderType );//3
Sobel(src, Dy,CV_32F, 0, 1,aperture_size, scale, 0,borderType );//为什么来个这么大的scale？？
}
else
{
Scharr(src, Dx,CV_32F, 1, 0, scale, 0,borderType );
Scharr(src, Dy,CV_32F, 0, 1, scale, 0,borderType );
}
Size size =src.size();
Mat cov( size,CV_32FC3 ); //dx^2,dxdy,dy^2
int i, j;
for( i = 0; i < size.height; i++ )
{
float* cov_data = (float*)(cov.data + i*cov.step);
constfloat* dxdata = (constfloat*)(Dx.data + i*Dx.step);
constfloat* dydata = (constfloat*)(Dy.data + i*Dy.step);
for( j = 0; j < size.width; j++ )
{
float dx = dxdata[j];
float dy = dydata[j];
cov_data[j*3] = dx*dx;
cov_data[j*3+1] = dx*dy;
cov_data[j*3+2] = dy*dy;
}
}
boxFilter(cov, cov, cov.depth(),Size(block_size,block_size),Point(-1,-1),false,borderType );
anchor – anchor point;default value Point(-1,-1) means that the anchor is at the kernel center.
//改成Gaussian滤波
//GaussianBlur(cov, cov, Size(5, 5), 0,0 );
if( op_type == MINEIGENVAL )
calcMinEigenVal( cov, eigenv );
elseif( op_type == HARRIS )
calcHarris( cov, eigenv, k );
elseif( op_type == EIGENVALSVECS )
calcEigenValsVecs( cov, eigenv );
}
}
calcHarris(constMat&_cov,Mat&_dst,doublek )
{
……………………
for( ; j < size.width; j++ )
{
float a = cov[j*3];
float b = cov[j*3+1];
float c = cov[j*3+2];
dst[j] = (float)(a*c - b*b -k*(a + c)*(a + c));//R = det(M)-k*trace(M)
}
………………
}
Note:matlab实现可参见《现代数字图像处理技术提高及应用案例详解（MATLAB版）》-赵小川