教你初步了解KMP算法
教你初步了解KMP算法
作者: July 、saturnma、上善若水。 时间; 二零一一年一月一日
-----------------------
本文参考:数据结构(c语言版) 李云清等编著、算法导论
引言:
在文本编辑中,我们经常要在一段文本中某个特定的位置找出 某个特定的字符或模式。
由此,便产生了字符串的匹配问题。
本文由简单的字符串匹配算法开始,再到KMP算法,由浅入深,教你从头到尾彻底理解KMP算法。
来看算法导论一书上关于此字符串问题的定义:
假设文本是一个长度为n的数组T[1...n],模式是一个长度为m<=n的数组P[1....m]。
进一步假设P和T的元素都是属于有限字母表Σ.中的字符。
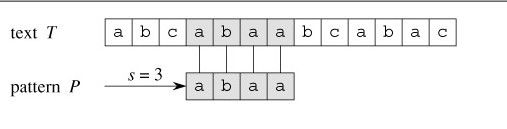
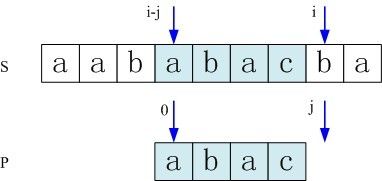
依据上图,再来解释下字符串匹配问题。目标是找出所有在文本T=abcabaabcaabac中的模式P=abaa所有出现。
该模式仅在文本中出现了一次,在位移s=3处。位移s=3是有效位移。
第一节、简单的字符串匹配算法
简单的字符串匹配算法用一个循环来找出所有有效位移,
该循环对n-m+1个可能的每一个s值检查条件P[1....m]=T[s+1....s+m]。
NAIVE-STRING-MATCHER(T, P)
1 n ← length[T]
2 m ← length[P]
3 for s ← 0 to n - m
4 do if P[1 ‥ m] = T[s + 1 ‥ s + m]
//对n-m+1个可能的位移s中的每一个值,比较相应的字符的循环必须执行m次。
5 then print "Pattern occurs with shift" s
简单字符串匹配算法,上图针对文本T=acaabc 和模式P=aab。
上述第4行代码,n-m+1个可能的位移s中的每一个值,比较相应的字符的循环必须执行m次。
所以,在最坏情况下,此简单模式匹配算法的运行时间为O((n-m+1)m)。
--------------------------------
下面我再来举个具体例子,并给出一具体运行程序:
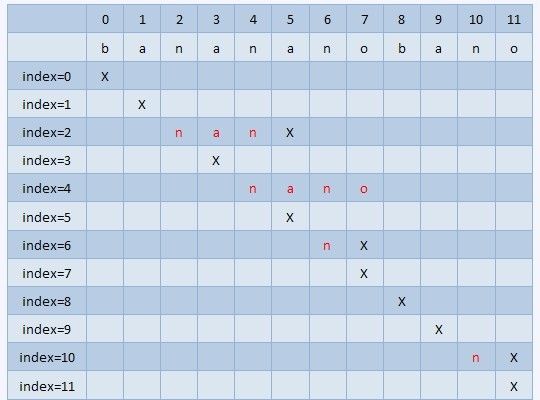
对于目的字串target是banananobano,要匹配的字串pattern是nano,的情况,
下面是匹配过程,原理很简单,只要先和target字串的第一个字符比较,
如果相同就比较下一个,如果不同就把pattern右移一下,
之后再从pattern的每一个字符比较,这个算法的运行过程如下图。
//index表示的每n次匹配的情形。
#include<iostream>
#include<string>
using namespace std;
int match(const string& target,const string& pattern)
{
int target_length = target.size();
int pattern_length = pattern.size();
int target_index = 0;
int pattern_index = 0;
while(target_index < target_length && pattern_index < pattern_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else
{
target_index -= (pattern_index-1);
pattern_index = 0;
}
}
if(pattern_index == pattern_length)
{
return target_index - pattern_length;
}
else
{
return -1;
}
}
int main()
{
cout<<match("banananobano","nano")<<endl;
return 0;
}
//运行结果为4。
上面的算法进间复杂度是O(pattern_length*target_length),
我们主要把时间浪费在什么地方呢,
观查index =2那一步,我们已经匹配了3个字符,而第4个字符是不匹配的,这时我们已经匹配的字符序列是nan,
此时如果向右移动一位,那么nan最先匹配的字符序列将是an,这肯定是不能匹配的,
之后再右移一位,匹配的是nan最先匹配的序列是n,这是可以匹配的。
如果我们事先知道pattern本身的这些信息就不用每次匹配失败后都把target_index回退回去,
这种回退就浪费了很多不必要的时间,如果能事先计算出pattern本身的这些性质,
那么就可以在失配时直接把pattern移动到下一个可能的位置,
把其中根本不可能匹配的过程省略掉,
如上表所示我们在index=2时失配,此时就可以直接把pattern移动到index=4的状态,
kmp算法就是从此出发。
第二节、KMP算法
2.1、 覆盖函数(overlay_function)
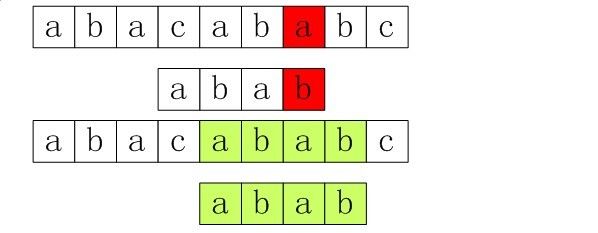
覆盖函数所表征的是pattern本身的性质,可以让为其表征的是pattern从左开始的所有连续子串的自我覆盖程度。
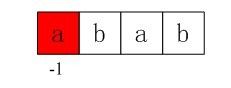
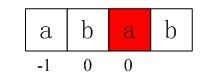
比如如下的字串,abaabcaba
由于计数是从0始的,因此覆盖函数的值为0说明有1个匹配,对于从0还是从来开始计数是偏好问题,
具体请自行调整,其中-1表示没有覆盖,那么何为覆盖呢,下面比较数学的来看一下定义,比如对于序列
a0a1...aj-1 aj
要找到一个k,使它满足
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
而没有更大的k满足这个条件,就是说要找到尽可能大k,使pattern前k字符与后k字符相匹配,k要尽可能的大,
原因是如果有比较大的k存在,而我们选择较小的满足条件的k,
那么当失配时,我们就会使pattern向右移动的位置变大,而较少的移动位置是存在匹配的,这样我们就会把可能匹配的结果丢失。
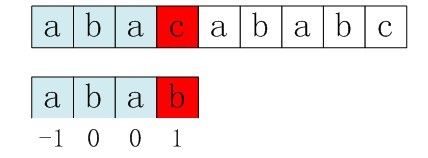
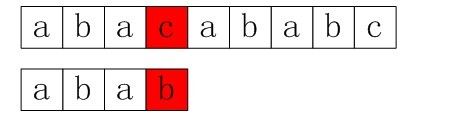
比如下面的序列,
在红色部分失配,正确的结果是k=1的情况,把pattern右移4位,如果选择k=0,右移5位则会产生错误。
计算这个overlay函数的方法可以采用递推,可以想象如果对于pattern的前j个字符,如果覆盖函数值为k
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
则对于pattern的前j+1序列字符,则有如下可能
⑴ pattern[k+1]==pattern[j+1] 此时overlay(j+1)=k+1=overlay(j)+1
⑵ pattern[k+1]≠pattern[j+1] 此时只能在pattern前k+1个子符组所的子串中找到相应的overlay函数,h=overlay(k),如果此时pattern[h+1]==pattern[j+1],则overlay(j+1)=h+1否则重复(2)过程.
下面给出一段计算覆盖函数的代码:
#include<iostream>
#include<string>
using namespace std;
void compute_overlay(const string& pattern)
{
const int pattern_length = pattern.size();
int *overlay_function = new int[pattern_length];
int index;
overlay_function[0] = -1;
for(int i=1;i<pattern_length;++i)
{
index = overlay_function[i-1];
//store previous fail position k to index;
while(index>=0 && pattern[i]!=pattern[index+1])
{
index = overlay_function[index];
}
if(pattern[i]==pattern[index+1])
{
overlay_function[i] = index + 1;
}
else
{
overlay_function[i] = -1;
}
}
for(i=0;i<pattern_length;++i)
{
cout<<overlay_function[i]<<endl;
}
delete[] overlay_function;
}
int main()
{
string pattern = "abaabcaba";
compute_overlay(pattern);
return 0;
}
运行结果为:
-1
-1
0
0
1
-1
0
1
2
Press any key to continue
-------------------------------------
2.2、kmp算法
有了覆盖函数,那么实现kmp算法就是很简单的了,我们的原则还是从左向右匹配,但是当失配发生时,我们不用把target_index向回移动,target_index前面已经匹配过的部分在pattern自身就能体现出来,只要动pattern_index就可以了。
当发生在j长度失配时,只要把pattern向右移动j-overlay(j)长度就可以了。
如果失配时pattern_index==0,相当于pattern第一个字符就不匹配,
这时就应该把target_index加1,向右移动1位就可以了。
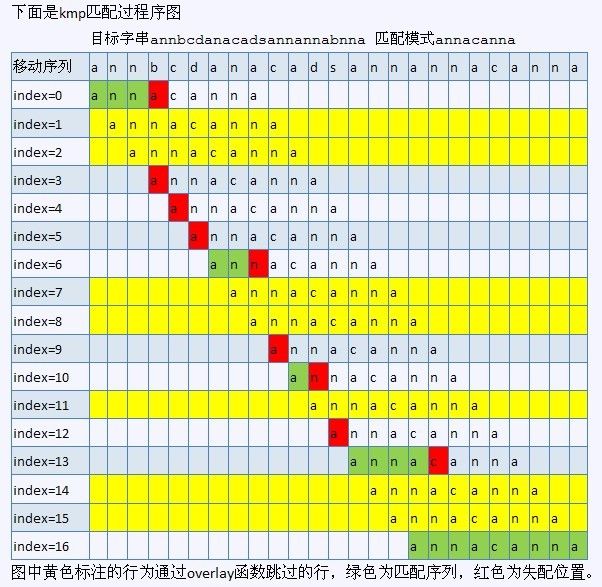
ok,下图就是KMP算法的过程(红色即是采用KMP算法的执行过程):
另一作者saturnman发现,在上述KMP匹配过程图中,index=8和index=11处画错了。还有,anaven也早已发现,index=3处也画错了。非常感谢。但图已无法修改,见谅。
KMP 算法可在O(n+m)时间内完成全部的串的模式匹配工作。
ok,最后给出KMP算法实现的c++代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int kmp_find(const string& target,const string& pattern)
{
const int target_length = target.size();
const int pattern_length = pattern.size();
int * overlay_value = new int[pattern_length];
overlay_value[0] = -1;
int index = 0;
for(int i=1;i<pattern_length;++i)
{
index = overlay_value[i-1];
while(index>=0 && pattern[index+1]!=pattern[i])
{
index = overlay_value[index];
}
if(pattern[index+1]==pattern[i])
{
overlay_value[i] = index +1;
}
else
{
overlay_value[i] = -1;
}
}
//match algorithm start
int pattern_index = 0;
int target_index = 0;
while(pattern_index<pattern_length&&target_index<target_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else if(pattern_index==0)
{
++target_index;
}
else
{
pattern_index = overlay_value[pattern_index-1]+1;
}
}
if(pattern_index==pattern_length)
{
return target_index-pattern_index;
}
else
{
return -1;
}
delete [] overlay_value;
}
int main()
{
string source = " annbcdanacadsannannabnna";
string pattern = " annacanna";
cout<<kmp_find(source,pattern)<<endl;
return 0;
}
//运行结果为 -1.
第三节、kmp算法的来源
kmp如此精巧,那么它是怎么来的呢,为什么要三个人合力才能想出来。其实就算没有kmp算法,人们在字符匹配中也能找到相同高效的算法。这种算法,最终相当于kmp算法,只是这种算法的出发点不是覆盖函数,不是直接从匹配的内在原理出发,而使用此方法的计算的覆盖函数过程序复杂且不易被理解,但是一但找到这个覆盖函数,那以后使用同一pattern匹配时的效率就和kmp一样了,其实这种算法找到的函数不应叫做覆盖函数,因为在寻找过程中根本没有考虑是否覆盖的问题。
说了这么半天那么这种方法是什么呢,这种方法是就大名鼎鼎的确定的有限自动机(Deterministic finite state automaton DFA),DFA可识别的文法是3型文法,又叫正规文法或是正则文法,既然可以识别正则文法,那么识别确定的字串肯定不是问题(确定字串是正则式的一个子集)。对于如何构造DFA,是有一个完整的算法,这里不做介绍了。在识别确定的字串时使用DFA实在是大材小用,DFA可以识别更加通用的正则表达式,而用通用的构建DFA的方法来识别确定的字串,那这个overhead就显得太大了。
kmp算法的可贵之处是从字符匹配的问题本身特点出发,巧妙使用覆盖函数这一表征pattern自身特点的这一概念来快速直接生成识别字串的DFA,因此对于kmp这种算法,理解这种算法高中数学就可以了,但是如果想从无到有设计出这种算法是要求有比较深的数学功底的。
第四节、精确字符匹配的常见算法的解析
KMP算法:
KMP就是串匹配算法
运用自动机原理
比如说
我们在S中找P
设P={ababbaaba}
我们将P对自己匹配
下面是求的过程:{依次记下匹配失败的那一位}
[2]ababbaaba
.......ababbaaba[1]
[3]ababbaaba
.........ababbaaba[1]
[4]ababbaaba
.........ababbaaba[2]
[5]ababbaaba
.........ababbaaba[3]
[6]ababbaaba
................ababbaaba[1]
[7]ababbaaba
................ababbaaba[2]
[8]ababbaaba
..................ababbaaba[2]
[9]ababbaaba
..................ababbaaba[3]
得到Next数组『0,1,1,2,3,1,2,2,3』
主过程:
[1]i:=1 j:=1
[2]若(j>m)或(i>n)转[4]否则转[3]
[3]若j=0或a[i]=b[j]则【inc(i)inc(j)转[2]】否则【j:=next[j]转2】
[4]若j>m则return(i-m)否则return -1;
若返回-1表示失败,否则表示在i-m处成功
BM算法也是一种快速串匹配算法,KMP算法的主要区别是匹配操作的方向不同。虽然T右移的计算方法却发生了较大的变化。
为方便讨论,T="dist :c->{dist称为滑动距离函数,它给出了正文中可能出现的任意字符在模式中的位置。函数 m – j j为 dist(m+1 若c = tm
例如,pattern",则p)a)t)dist(= 2,r)n)BM算法的基本思想是:假设将主串中自位置i + dist(si)位置开始重新进行新一轮的匹配,其效果相当于把模式和主串向右滑过一段距离si),即跳过si)个字符而无需进行比较。
下面是一个S ="T="BM算法可以大大加快串匹配的速度。
下面是KMP算法部分,把调用BM函数便可。
view plain
- #include <iostream>
- using namespace std;
- int Dist(char *t,char ch)
- {
- int len = strlen(t);
- int i = len - 1;
- if(ch == t[i])
- return len;
- i--;
- while(i >= 0)
- {
- if(ch == t[i])
- return len - 1 - i;
- else
- i--;
- }
- return len;
- }
- int BM(char *s,char *t)
- {
- int n = strlen(s);
- int m = strlen(t);
- int i = m-1;
- int j = m-1;
- while(j>=0 && i<n)
- {
- if(s[i] == t[j])
- {
- i--;
- j--;
- }
- else
- {
- i += Dist(t,s[i]);
- j = m-1;
- }
- }
- if(j < 0)
- {
- return i+1;
- }
- return -1;
- }
Horspool算法
这个算法是由R.Nigel Horspool在1980年提出的。其滑动思想非常简单,就是从后往前匹配模式串,若在某一位失去匹配,此位对应的文本串字符为c,那就将模式串向右滑动,使模式
串之前最近的c对准这一位,再从新从后往前检查。那如果之前找不到c怎么办?那好极了,直接将整个模式串滑过这一位。
例如:文本串:abdabaca
模式串:baca倒数第2位失去匹配,模式串之前又没有d,那模式串就可以整个滑过,变成这样:
文本串:abdabaca
模式串: baca发现倒数第1位就失去匹配,之前1位有c,那就向右滑动1位:
文本串:abdabaca
模式串: baca实现代码:
view plain
- #include <iostream>
- #include <vector>
- #include <string>
- #include <cstdlib>
- using namespace std;
- int Horspool_match(const string & S,const string & M,int pos)
- {
- int S_len = S.size();
- int M_len = M.size();
- int Mi = M_len-1,Si= pos+Mi; //这里的串的第1个元素下标是0
- if( (S_len-pos) < M_len )
- return -1;
- while ( (Mi>-1) && (Si<S_len) )
- {
- if (S[Si] == M[Mi])
- {
- --Mi;
- --Si;
- }
- else
- {
- do
- {
- Mi--;
- }
- while( (S[Si]!=M[Mi]) || (Mi>-1) );
- Mi = M_len - 1;
- Si += M_len - 1;
- }
- }
- if(Si < S_len)
- return(Si + 1);
- else
- return -1;
- }
- int main( )
- {
- string S="abcdefghabcdefghhiijiklmabc";
- string T="hhiij";
- int pos = Horspool_match(S,T,3);
- cout<<"/n"<<pos<<endl;
- system("pause");
- return 0;
- }
SUNDAY算法:
BM算法的改进的算法SUNDAY--Boyer-Moore-Horspool-Sunday Aglorithm
BM算法优于KMP
SUNDAY 算法描述:
字符串查找算法中,最著名的两个是KMP算法(Knuth-Morris-Pratt)和BM算法(Boyer-Moore)。两个算法在最坏情况下均具有线性的查找时间。但是在实用上,KMP算法并不比最简单的c库函数strstr()快多少,而BM算法则往往比KMP算法快上3-5倍。但是BM算法还不是最快的算法,这里介绍一种比BM算法更快一些的查找算法即Sunday算法。
例如我们要在"substring searching algorithm"查找"search",刚开始时,把子串与文本左边对齐:
substring searching algorithm
search
^
结果在第二个字符处发现不匹配,于是要把子串往后移动。但是该移动多少呢?这就是各种算法各显神通的地方了,最简单的做法是移动一个字符位置;KMP是利用已经匹配部分的信息来移动;BM算法是做反向比较,并根据已经匹配的部分来确定移动量。这里要介绍的方法是看紧跟在当前子串之后的那个字符(上图中的 'i')。
显然,不管移动多少,这个字符是肯定要参加下一步的比较的,也就是说,如果下一步匹配到了,这个字符必须在子串内。所以,可以移动子串,使子串中的最右边的这个字符与它对齐。现在子串'search'中并不存在'i',则说明可以直接跳过一大片,从'i'之后的那个字符开始作下一步的比较,如下图:
substring searching algorithm
search
^
比较的结果,第一个字符就不匹配,再看子串后面的那个字符,是'r',它在子串中出现在倒数第三位,于是把子串向前移动三位,使两个'r'对齐,如下:
substring searching algorithm
search
^
哈!这次匹配成功了!回顾整个过程,我们只移动了两次子串就找到了匹配位置,可以证明,用这个算法,每一步的移动量都比BM算法要大,所以肯定比BM算法更快。
view plain
- #include<iostream>
- #include<fstream>
- #include<vector>
- #include<algorithm>
- #include<string>
- #include<list>
- #include<functional>
- using namespace std;
- int main()
- {
- char *text=new char[100];
- text="substring searching algorithm search";
- char *patt=new char[10];
- patt="search";
- size_t temp[256];
- size_t *shift=temp;
- size_t patt_size=strlen(patt);
- cout<<"size : "<<patt_size<<endl;
- for(size_t i=0;i<256;i++)
- *(shift+i)=patt_size+1;//所有值赋于7,对这题而言
- for(i=0;i<patt_size;i++)
- *(shift+unsigned char(*(patt+i) ) )=patt_size-i;
- /* // 移动3步-->shift['r']=6-3=3;移动三步
- //shift['s']=6步,shitf['e']=5以此类推
- */
- size_t text_size=strlen(text);
- size_t limit=text_size-i+1;
- for(i=0;i<limit;i+=shift[text[i+patt_size] ] )
- if(text[i]==*patt)
- {
- /* ^13--这个r是位,从0开始算
- substring searching algorithm
- search
- searching-->这个s为第10位,从0开始算
- 如果第一个字节匹配,那么继续匹配剩下的
- */
- char* match_text=text+i+1;
- size_t match_size=1;
- do{
- if(match_size==patt_size)
- cout<<"the no is "<<i<<endl;
- }while( (*match_text++)==patt[match_size++] );
- }
- cout<<endl;
- return 0;
- }
- //运行结果如下:
- /*
- size : 6
- the no is 10
- the no is 30
- Press any key to continue
- */
在此之前,说明下写作本文的目的:1、之前承诺过,这篇文章六、教你从头到尾彻底理解KMP算法、updated之后,KMP算法会写一个续集;2、写这个kMP算法的文章很多很多,但真正能把它写明白的少之又少;3、这个KMP算法曾经困扰过我很长一段时间。我也必须让读者真真正正彻彻底底的理解它。希望,我能做到。
ok,子串的定位操作通常称做串的模式匹配,是各种串处理系统中最重要的操作之一.在很多应用中都会涉及子串的定位问题,如普通的字符串查找问题.如果我们把模式匹配的串看成一字节流的话,那应用空间一下子就广阔了很多,如HTTP协议里就是字节流,有各种关键的字节流字段,对HTTP数据进行解释就需要用到模式匹配算法.
本文是试图清楚的讲解模式匹配算法里两个最为重要的算法:KMP与BM算法,这两个算法都较为高效,特别是BM算法在工程用应用得非常多的,然而网上很多BM算法都不算准确的。本文开始讲解简单回溯字符串匹配算法,后面过渡到KMP算法,最后再过渡到BM算法,希望能够讲得明白易懂。
模式匹配问题抽象为:给定主串S(Source,长度为n),模式串P(Pattern, 长度为m),要求查找出P在S中出现的位置,一般即为第一次出现的位置,如果S中没有P子串,返回相应的结果。如下图0查找成功,则查找结果返回2:
图0 字符串查找
本文,接下来,将一步一步讲解KMP算法。希望看完本文后,读者日后对Kmp算法能做到胸中丘壑自成。文章有任何错误,烦请一定指出来。谢谢。
第一部分、KMP算法
- 1、回溯法字符串匹配算法
回溯法字符串匹配算法就是用一个循环来找出所有有效位移,该循环对n-m+1个可能的位移中的每一个index值,检查条件为P[0…m-1]= S[index…index+m-1](因为模式串的长度是m,索引范围为0…m-1)。
S 0......index.... index+m-1 (src[i]表示)
P 0 .... m-1 (patn[j]表示)
- //代码1-1
- //int search(char const*, int, char const*, int)
- //查找出模式串patn在主串src中第一次出现的位置
- //plen为模式串的长度
- //返回patn在src中出现的位置,当src中并没有patn时,返回-1
- int search(char const* src, int slen, char const* patn, int plen)
- {
- int i = 0, j = 0;
- while( i < slen && j < plen )
- {
- if( src[i] == patn[j] ) //如果相同,则两者++,继续比较
- {
- ++i;
- ++j;
- }
- else
- {
- //否则,指针回溯,重新开始匹配
- i = i - j + 1; //退回到最开始时比较的位置
- j = 0;
- }
- }
- if( j >= plen )
- return i - plen; //如果字符串相同的长度大于模式串的长度,则匹配成功
- else
- return -1;
- }
该算法思维比较简单(但也常被一些公司做为面试题),很容易分析出本算法的时间复杂度为O(pattern_length*target_length),我们主要是把时间浪费在什么地方呢,相信,你已经看到上面的代码注释中有这么一句话:“指针回溯,重新开始匹配”,这句话的意思就是好比我们乘坐一辆火车已经离站好远了,后来火车司机突然对全部乘客说,你们搭错了列车,要换一辆火车。也就是说在咱们的字符串匹配中,本来已经比较到前面的字符去了,现在又要回到原来的某一个位置重新开始一个个的比较。这就是问题的症结所在。
在继续分析之前,咱们来思考这样一个问题:为什么快排或者堆排序比直接的选择排序快?直接的选择排序,每次都是重复的比较数值的大小,每扫描一次,只得出一个最大(小值),再没有其它的结果信息能给下一次扫描带来便捷。我们看看快排,每扫一次,将数据按某一值分成了两边,至少有右边的数据都大于左边的数据,所以在比较的时候,下一次就不用比较了。再看看堆排序,建堆的过程也是O(n)的比较,但比较的结果得到了最大(小)堆这种三角关系,之后的比较就不用再每一个都需要比较了。
由上述思考,咱们总结出了一点优化的归律:采用一种简单的数据结构或者方式,将每次重复性的工作得到的信息记录得尽量多,方便下一次做同样的工作,这样将带来一定的优化(个人性总结)。
回溯法做的多余的工作
以下给出一个例子来启发,如下图2:
图1-1 回溯法的一个示例
可以看出当匹配到g与h的时候,不匹配了(后面,你将看到,KMP算法会直接从匹配失效的位置,即g位置处重新开始匹配,这就是KMP的高效之处),模式串的下一个位置该怎么移动,需要回溯到第二个位置如:
图1-2 回溯到第二个位置
在第二个位置发现还是不匹配,便再次回溯到第三个位置:
图1-3 回溯到第三个位置
其实可以分析一下模式串里,每个字符都不相同,如果前面有匹配成功,那移动一位或者几位后,是不可能匹配成功的。
启示:模式串里有蕴含信息的,可以简化扫描。接下来深入的讨论另一算法KMP算法。
- 2、KMP算法的简介
KMP算法就是一种基于分析模式串蕴含信息的改进算法,是D.E.Knuth与V.R.Pratt和J.H.Morris同时发现的,因此人们称它为KMP算法。
咱们还是以上面的例子为例,如下图2-1:图2-1 KMP算法的一个例子
如果是普通的匹配算法,那么接下来,模式串的下一个匹配将如上一节读者所看到的那样,回溯到第二个位置b处。而KMP算法会怎么做呢?KMP算法会直接把模式串移到匹配失效的位置上,如下图2-2,g处:
图2-2 直接移到匹配失效的位置g处
Ok,咱们下面再看一个例子,如下图2-3/4:图2- 3/4 另一个例子
我们为什么要这么做呢?如上面的例子,每个字符都不相同,如果前面有匹配成功,那移动一位或者几位后,是不可能匹配成功的,所以我们完全可以就模式串的特点来决定下一次匹配从哪个地方开始。
问题转化成为对于模式串P,当P[j](0<=j<m)与主串匹配到第i个字符(S[i], 0<=i<n)失败的时候,接下来应该用什么位置的字符P[j_next](我们设j_next即匹配失效后下一个匹配的位置)与主串S[i]开始匹配呢?重头开始匹配?No,在P[j]!=S[i]之前的时候,有S[i-j…i-1]与P[0…j-1]是相同的,所以S不用回溯,因为S[i]前面的值都已经确切的知道了。S 0 i-j..i-1 i .... n (S[i]表示,S[i]处匹配失败)
P 0.. j-1 j.. m (P[j]表示,要找下一个匹配的位置P[j_next])以上,在P[j]!=S[i]之前的时候,有S[i-j…i-1]与P[0…j-1]是匹配即相同的字符,各自都用下划线表示。
咱们先写下算法,你将看到,其实KMP算法的代码非常简洁,只有20来行而已。如下描述为:
- //代码2-1
- //int kmp_seach(char const*, int, char const*, int, int const*, int pos) KMP模式匹配函数
- //输入:src, slen主串
- //输入:patn, plen模式串
- //输入:nextval KMP算法中的next函数值数组
- int kmp_search(char const* src, int slen, char const* patn, int plen, int const* nextval, int pos)
- {
- int i = pos;
- int j = 0;
- while ( i < slen && j < plen )
- {
- if( j == -1 || src[i] == patn[j] )
- {
- ++i;
- ++j; //匹配成功,就++,继续比较。
- }
- else
- {
- j = nextval[j];
- //当在j处,P[j]与S[i]匹配失败的时候直接用patn[nextval[j]]继续与S[i]比较,
- //所以,Kmp算法的关键之处就在于怎么求这个值拉,
- //即匹配失效后下一次匹配的位置。下面,具体阐述。
- }
- }
- if( j >= plen )
- return i-plen;
- else
- return -1;
- }
- 3、如何求next数组各值
现在的问题是p[j_next]中的j_next即上述代码中的nextval[j]怎么求。
当匹配到S[i] != P[j]的时候有 S[i-j…i-1] = P[0…j-1]. 如果下面用j_next去匹配,则有P[0…j_next-1] = S[i-j_next…i-1] = P[j-j_next…j-1]。此过程如下图3-1所示。当匹配到S[i] != P[j]时,S[i-j…i-1] = P[0…j-1]:
S: 0 … i-j … i-1 i …
P: 0 … j-1 j …
如果下面用j_next去匹配,则有P[0…j_next-1] = S[i-j_next…i-1] = P[j-j_next…j-1]。
所以在P中有如下匹配关系(获得这个匹配关系的意义是用来求next数组):P: 0 … j-j_next .…j-1_ …
P: 0 … .j_next-1 …
所以,根据上面两个步骤,推出下一匹配位置j_next:
S: 0 … i-j … i-j_next … i-1 i …
P: 0 … j_next-1 j_next …
图3-1 求j-next(最大的值)的三个步骤
下面,我们用变量k来代表求得的j_next的最大值,即k表示这S[i]、P[j]不匹配时P中下一个用来匹配的位置,使得P[0…k-1] = P[j-k…j-1],而我们要尽量找到这个k的最大值。如你所见,当匹配到S[i] != P[j]的时候,最大的k为1(当S[i]与P[j]不匹配时,用P[k]与S[i]匹配,即P[1]和S[i]匹配,因为P[0]=P[2],所以最大的k=1)。
图3-2 j_next=1,即最大的k的值为1
如上图3-1,当P[3]!=S[i],而P[0]=P[2](当P[3]!=S[i],而P[0]=P[2],P[2]=S[i-1],所以肯定有P[0]=S[i-1])),所以只需比较P[1]与S[i]就可以了,即k是P可以跳过比较的最大长度,换句话说,就是k能标示出S[i]与P[j]不匹配时P的下一个匹配的位置。
图3-3 第二步匹配中,跳过P[0](a),只需要比较 P[1]与S[3](b)了
也就是说,如上图3-2,在第一次匹配中,就是因为S[2]=P[0],所以在下一次匹配中,只需要比较S[3]=P[1],跳过了几步?一步。那么k等于多少?k=1。即把 P 右移两个位置后,P[0]与S[2]不必再比较,因为前一步已经得出他们相等。所以,此时,只需要比较 P[1]与S[3]了。
接下来的问题是,怎么求最大的数k使得p[0…k-1] = p[j-k…j-1]呢。这就是KMP算法中最核心的问题,即怎么求next数组的各元素的值?只有真正弄懂了这个next数组的求法,你才能彻底明白KMP算法到底是怎么一回事。
那么,怎么求这个next数组呢?咱们一步一步来考虑。
求最大的数k使得P[0…k-1] = P[j-k…j-1],一个直接的办法是对于j,从P[j-1]往回查,看是否有满足P[0…k-1] = P[j-k…j-1]的k存在,而且还要最大的一个k。下面咱们换一个角度思考。
当P[j+1]与S[i+1]不匹配时,分两种情况求next数组(注:以下皆有k=next[j]):
- P[j] = p[k], 那么next[j+1]=k+1,这个很容易理解。采用递推的方式求出next[j+1]=k+1(代码3-1的if部分)。
- P[j] != p[k],那么next[j+1]=next[k]+1(代码3-1的else部分)
稍后,你将看到,由这个方法得出的next值还不是最优的,也就是说是不能允许P[j]=P[next[j]]出现的。ok,请跟着我们一步一步登上山顶,不要试图一步登天,那是不可能的。由以上,可得如下代码:
- //代码3-1,稍后,你将由下文看到,此求next数组元素值的方法有错误
- void get_next(char const* ptrn, int plen, int* nextval)
- {
- int i = 0;
- nextval[i] = -1;
- int j = -1;
- while( i < plen-1 )
- {
- if( j == -1 || ptrn[i] == ptrn[j] ) //循环的if部分
- {
- ++i;
- ++j;
- nextval[i] = j;
- }
- else //循环的else部分
- j = nextval[j]; //递推
- }
- }
next数组求值的验证
上述求next数组各值的方法(代码)是否正确呢?我们来举一个例子,应用上述的get_next函数来试验一下,即具体求解一下next数组各元素的值(通过下面的验证,我们将看到上面的求next数组的方法是有问题的,而后我们会在下文的第4小节具体修正上述求next数组的方法)。ok,请看:
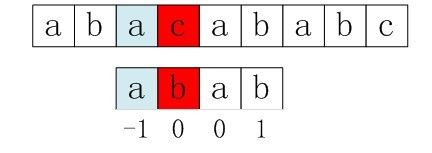
首先,模式串如下:字符串abab下面对应的数值即是已经求出的对应的nextval[i]值:
图3-4 求next数组各值的示例
接下来,咱们来具体解释下上面next数组中对应的各个nextval[i]的值是怎么求得来的,因为,理解KMP算法的关键就在于这个求next值的过程。Ok,如下,咱们再次引用一下上述求next数组各值的核心代码:int i = 0;
nextval[i] = -1;
int j = -1;
while( i < plen-1 )
{
if( j == -1 || ptrn[i] == ptrn[j] ) //循环的if部分
{
++i;
++j;
nextval[i] = j;
}
else //循环的else部分
j = nextval[j]; //递推
}所以,根据上面的代码,咱们首先要初始化nextval[0] = -1,我们得到第一个next数组元素值即-1(注意,咱们现在的目标是要求nextval[i]各个元素的值,i是数组的下标,为0.1.2.3);
图3-5 第一个next数组元素值-1
首先初始化:i = 0,j = -1,由于j == -1,进入上述函数中循环的if部分,++i得 i=1,++j得j=0,所以我们得到第二个next值即nextval[1] = 0;
图3-6 第二个next数组元素值0
i= 1,j = 0,由于不满足条件j == -1 || ptrn[i] == ptrn[j](第一个元素a与第二个元素b不相同,所以也不满足第2个条件),所以进入上述循环的else部分,得到j = nextval[j] = -1(原来的nextval[0]=-1并没有改变),得到i = 1,j = -1;此时,由于j == -1且i<plen-1依然成立,所以再次进入上述循环的if部分,++i的i=2,++j得j=0,所以得到第三个next值即nextval[2] = 0;
图3-7 第三个next数组元素值0
此时,i = 2,j = 0,由于ptrn[i] == ptrn[j](第1个元素和第3个元素都是a,相同,所以,虽然不满足j=-1的第1个条件,但满足第2个条件即ptrn[i] == ptrn[j]),进入循环的if部分,++i得i=3,++j得j=1,所以得到我们的第四个next值即nextval[3] = 1(由下文的第4小节,你将看到,求出的next数组之所以有误,问题就是出在这里。正确的解决办法是,如下文的第4小节所述,++i,++j之后,还得判断patn[i]与patn[j]是否相等,即杜绝出现P[j]=P[next[j]]这样的情况);
自此,我们得到了 nextval[i]数组的4个元素值,分别为-1,0,0,1。如下图3-8所示:图3-8 第四个next数组元素值1
求得了相应的next数组(本文约定,next数组是指一般意义的next数组,而nextval[i]则代表具体求解next数组各数值的意义)各值之后,接下来的一切工作就好办多了。
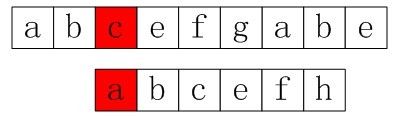
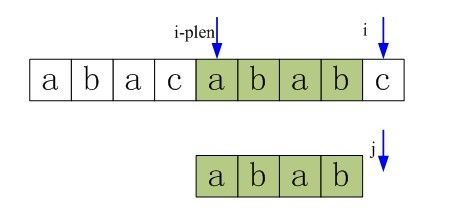
第一步:主串和模式串如下,由下图可以看到,我们在p[3]处匹配失败(即p[3]!=s[3])。
图3-9 第一步,在p[3]处匹配失败
第二步:接下来要用p[next[3]](看到了没,是该我们上面求得的next数组各值大显神通的时候了),即p[1]与s[3]匹配( 不要忘了,上面我们已经求得的nextval[i]数组的4个元素值,分别为-1,0,0,1)。但在p[1]处还是匹配失败(即p[1]!=s[3])。
图3-10 第二步,p[1]处还是匹配失败
第三步:接下来模式串指针指向下一位置next[1]=0处(注意此过程中主串指针是不动的),即模式串指针指向p[0],即用p[0]与s[3]匹配(看起来,好像是k步步减小,这就是咱们开头所讲到的怎么求最大的数k使得P[0…k-1] = [j-k…j-1])。而p[0]与s[3]还是不匹配。

图3-11 第三步,p[0]与s[3]还是不匹配
第四步:由于上述第三步中,P[0]与S[3]还是不匹配。此时i=3,j=nextval[0]=-1,由于满足条件j==-1,所以进入循环的if部分,++i=4,++j=0,即主串指针下移一个位置,从p[0]与s[4]处开始匹配。最后j==plen,跳出循环,输出结果i-plen=4(即字串第一次出现的位置)
图3-12 第四步,跳出循环,输出结果i-plen=4
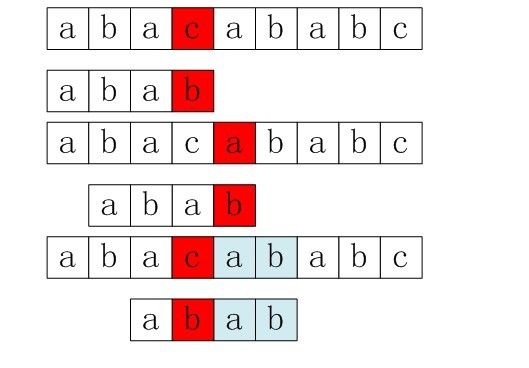
所以,综上,总结上述四步为:
- P[3]!=S[3],匹配失败;
- nextval[3]=1,所以P[1]继续与S[3]匹配,匹配失败;
- nextval[1]=0,所以P[0]继续与S[3]匹配,再次匹配失败;
- nextval[0]=-1,满足循环if部分条件j==-1,所以,++i,++j,主串指针下移一个位置,从P[0]与S[4]处开始匹配,最后j==plen,跳出循环,输出结果i-plen=4,算法结束。
不知,读者是否已看出,上面的匹配过程隐藏着一个不容忽略的问题,即有一个完全可以改进的地方。对的,问题就出现在上述过程的第二步。
观察上面的匹配过程,看匹配的第二步,在第一步的时候已有P[3]=b与S[3]=c不匹配,而下一步如果还是要让P[next[3]]=P[1]=b与s[3]=c匹配的话,那么结果很明显,还是肯定会匹配失败的。由此可以看出我们的next值还不是最优的,也就是说是不能允许P[j]=P[next[j]]出现的,即上面的求next值的算法需要修正。
也就是说上面求得的nextval[i]数组的4个元素值,分别为-1,0,0,1是有问题的。有什么问题呢?就是不容许出现这种情况P[j]=P[next[j]]。为什么?
好比上面的例子。请容许我再次引用上面例子中的两张图。在上面的第一步匹配中,我们已经得出P[3]=b是不等于S[3]=c的。而在上面的第二步匹配中,根据求得的nextval[i]数组值中的nextval[3]=1,即让P[1]重新与S[3]再次匹配。这不是明摆着有问题么?因为P[1]也等于b阿,而在第一步匹配中,我们已经事先得知b是不可能等于S[3]的。所以,第二步匹配之前就已注定是失败的。图3-13/14 求next数组各值的错误解法
这里读者理解可能有困难的是因为文中,时而next,时而nextval,把他们的思维搞混乱了。其实next用于表达数组索引,而nextval专用于表达next数组索引下的具体各值,区别细微。至于文中说不允许P
=P[next[j] ]出现,是因为已经有P
=b与S
匹配败,而P[next
]=P
=b,若再拿P[1]去与S
匹配则必败。
- 4、求解next数组各值的方法修正
那么,上面求解next数组各值的问题到底出现在哪儿呢?我们怎么才能摆脱掉这种情况呢?:即不能让P[j]=P[next[j]]成立成立。不能再出现上面那样的情况啊!即不能有这种情况出现:P[3]=b,而竟也有P[next[3]]=P[1]=b。
让我们再次回顾一下之前求next数组的函数代码:
- //引用之前上文第3小节中的有错误的求next的代码3-1。
- void get_next(char const* ptrn, int plen, int* nextval)
- {
- int i = 0;
- nextval[i] = -1;
- int j = -1;
- while( i < plen-1 )
- {
- if( j == -1 || ptrn[i] == ptrn[j] ) //循环的if部分
- {
- ++i;
- ++j;
- nextval[i] = j; //这里有问题
- }
- else //循环的else部分
- j = nextval[j]; //递推
- }
- }
由上面之前的代码,我们看到,在求next值的时候采用的是递推。这里的求法是有问题的。因为在s[i]!=p[j]的时候,如果p[j]=p[k](k=nextval[j],为之前的错误方法求得的next值),那么P[k]!=S[i],用之前的求法求得的next[j]==k,下一步直接导致匹配(S[i]与P[k]匹配)失败。
根据上面的分析,我们知道求next值的时候还要考虑P[j]与P[k]是否相等。当有P[j]=P[k]的时候,只能向前递推出一个p[j]!=p[k'],其中k'=next[next[j]]。修正的求next数组的get_nextval函数代码如下:
- //代码4-1
- //修正后的求next数组各值的函数代码
- void get_nextval(char const* ptrn, int plen, int* nextval)
- {
- int i = 0;
- nextval[i] = -1;
- int j = -1;
- while( i < plen-1 )
- {
- if( j == -1 || ptrn[i] == ptrn[j] ) //循环的if部分
- {
- ++i;
- ++j;
- //修正的地方就发生下面这4行
- if( ptrn[i] != ptrn[j] ) //++i,++j之后,再次判断ptrn[i]与ptrn[j]的关系
- nextval[i] = j; //之前的错误解法就在于整个判断只有这一句。
- else
- nextval[i] = nextval[j];
- }
- else //循环的else部分
- j = nextval[j];
- }
- }
举个例子,举例说明下上述求next数组的方法。
S a b a b a b c
P a b a b c
S[4] != P[4]
那么下一个和S[4]匹配的位置是k=2(也即P[next[4]])。此处的k=2也再次佐证了上文第3节开头处关于为了找到下一个匹配的位置时k的求法。上面的主串与模式串开头4个字符都是“abab”,所以,匹配失效后下一个匹配的位置直接跳两步继续进行匹配。
S a b a b a b c
P a b a b c
匹配成功P的next数组值分别为-1 0 -1 0 2
next数组各值怎么求出来的呢?分以下五步:
- 初始化:i=0,j=-1;
- i=1,j=0,进入循环esle部分,j=nextval[j]=nextval[0]=-1;
- 进入循环的if部分,++i,++j,i=2,j=0,因为ptrn[i]=ptrn[j]=a,所以nextval[2]=nextval[0]=-1;
- i=2, j=0, 由于ptrn[i]=ptrn[j],再次进入循环if部分,所以++i=3,++j=1,因为ptrn[i]=ptrn[j]=b,所以nextval[3]=nextval[1]=0;
- i=3,j=1,由于ptrn[i]=ptrn[j]=b,所以++i=4,++j=2,因为ptrn[i]!=ptrn[j],所以nextval[4]=2。
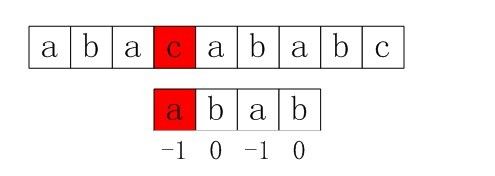
这样上例中模式串的next数组各值最终应该为:
图4-1 正确的next数组各值
next数组求解的具体过程如下:
初始化:nextval[0] = -1,我们得到第一个next值即-1.图4-2 第一个next值即-1
i = 0,j = -1,由于j == -1,进入上述循环的if部分,++i得i=1,++j得j=0,且ptrn[i] != ptrn[j](即a!=b)),所以得到第二个next值即nextval[1] = 0;
图4-3 第二个next值0
上面我们已经得到,i= 1,j = 0,由于不满足条件j == -1 || ptrn[i] == ptrn[j],所以进入循环的esle部分,得j = nextval[j] = -1;此时,仍满足循环条件,由于i = 1,j = -1,因为j == -1,再次进入循环的if部分,++i得i=2,++j得j=0,由于ptrn[i] == ptrn[j](即ptrn[2]=ptrn[0],也就是说第1个元素和第三个元素都是a),所以进入循环if部分内嵌的else部分,得到nextval[2] = nextval[0] = -1;
图4-4 第三个next数组元素值-1
i = 2,j = 0,由于ptrn[i] == ptrn[j],进入if部分,++i得i=3,++j得j=1,所以ptrn[i] == ptrn[j](ptrn[3]==ptrn[1],也就是说第2个元素和第4个元素都是b),所以进入循环if部分内嵌的else部分,得到nextval[3] = nextval[1] = 0;
图4-5 第四个数组元素值0
如果你还是没有弄懂上述过程是怎么一回事,请现在拿出一张纸和一支笔出来,一步一步的画下上述过程。相信我,把图画出来了之后,你一定能明白它的。
然后,我留一个问题给读者,为什么上述的next数组要那么求?有什么原理么?
- 5、利用求得的next数组各值运用Kmp算法
Ok,next数组各值已经求得,万事俱备,东风也不欠了。接下来,咱们就要应用求得的next值,应用KMP算法来匹配字符串了。还记得KMP算法是怎么一回事吗?容我再次引用下之前的KMP算法的代码,如下:
- //代码5-1
- //int kmp_seach(char const*, int, char const*, int, int const*, int pos) KMP模式匹配函数
- //输入:src, slen主串
- //输入:patn, plen模式串
- //输入:nextval KMP算法中的next函数值数组
- int kmp_search(char const* src, int slen, char const* patn, int plen, int const* nextval, int pos)
- {
- int i = pos;
- int j = 0;
- while ( i < slen && j < plen )
- {
- if( j == -1 || src[i] == patn[j] )
- {
- ++i;
- ++j;
- }
- else
- {
- j = nextval[j];
- //当匹配失败的时候直接用p[j_next]与s[i]比较,
- //下面阐述怎么求这个值,即匹配失效后下一次匹配的位置
- }
- }
- if( j >= plen )
- return i-plen;
- else
- return -1;
- }
我们上面已经求得的next值,如下:
图5-1 求得的正确的next数组元素各值
以下是匹配过程,分三步:
第一步:主串和模式串如下,S[3]与P[3]匹配失败。图5-2 第一步,S[3]与P[3]匹配失败
第二步:S[3]保持不变,P的下一个匹配位置是P[next[3]],而next[3]=0,所以P[next[3]]=P[0],即P[0]与S[3]匹配。在P[0]与S[3]处匹配失败。图5-3 第二步,在P[0]与S[3]处匹配失败
第三步:与上文中第3小节末的情况一致。由于上述第三步中,P[0]与S[3]还是不匹配。此时i=3,j=nextval[0]=-1,由于满足条件j==-1,所以进入循环的if部分,++i=4,++j=0,即主串指针下移一个位置,从P[0]与S[4]处开始匹配。最后j==plen,跳出循环,输出结果i-plen=4(即字串第一次出现的位置),匹配成功,算法结束。
图5-4 第三步,匹配成功,算法结束
所以,综上,总结上述三步为:
- 开始匹配,直到P[3]!=S[3],匹配失败;
- nextval[3]=0,所以P[0]继续与S[3]匹配,再次匹配失败;
- nextval[0]=-1,满足循环if部分条件j==-1,所以,++i,++j,主串指针下移一个位置,从P[0]与S[4]处开始匹配,最后j==plen,跳出循环,输出结果i-plen=4,算法结束。
与上文中第3小节的四步匹配相比,本节运用修正过后的next数组,去掉了第3小节的第2个多余步骤的nextval[3]=1,所以P[1]继续与S[3]匹配,匹配失败(缘由何在?因为与第3小节的next数组相比,此时的next数组中nextval[3]已等于0)。所以,才只需要三个匹配步骤了。
ok,KMP算法已宣告完结,希望已经了却了心中的一块结石。毕竟,这个KMP算法此前也困扰了我很长一段时间。耐心点,慢慢来,总会搞懂的。闲不多说,接下来,咱们开始介绍BM算法。
第二部分、BM算法
1、简单的后比对算法
为了更好的理解BM算法,我分三步引入BM算法。首先看看下面的一个字符串匹配算法,它与前面的回溯法差不多,看看差别在哪儿。
- /*! int search_reverse(char const*, int, char const*, int)
- */bref 查找出模式串patn在主串src中第一次出现的位置
- */return patn在src中出现的位置,当src中并没有patn时,返回-1
- */
- int search_reverse(char const* src, int slen, char const* patn, int plen)
- {
- int s_idx = plen, p_idx;
- if (plen == 0)
- return -1;
- while (s_idx <= slen)//计算字符串是否匹配到了尽头
- {
- p_idx = plen;
- while (src[--s_idx] == patn[--p_idx])//开始匹配
- {
- //if (s_idx < 0)
- //return -1;
- if (p_idx == 0)
- {
- return s_idx;
- }
- }
- s_idx += (plen - p_idx)+1;
- }
- return -1
- }
仔细分析上面的代码,可以看出该算法的思路是从模式串的后面向前面匹配的,如果后面的几个都不匹配了,就可以直接往前面跳了,直觉上这样匹配更快些。是否真是如此呢?请先看下面的例子。
上面是详细的算法流程,接下来我们就用上面的例子,来引出坏2、字符规则,3、最好后缀规则,最终引出4、BM算法。
2、坏字符规则
在上面的例子里面,第一步的时候,S[3] = ‘c’ != P[3],下一步应该当整个模式串移过S[3]即可,因为S[3]已经不可能与P中的任何一个部分相匹配了。那是不是只是对于P中不存在的字符就这样直接跳过呢,如果P中存在的字符该怎么定位呢?
如模式串为P=”acab”,基于坏字符规则匹配步骤分解图如下:
从上面的例子可以看出,我们需要建一张表,表示P中字符存在的情况,不存在,则s_idx直接加上plen跳过该字符,如果存在,则需要找到从后往前最近的一个字符对齐匹配,如上面的例子便已经说明了坏字符规则匹配方法.
再看下面的例子:
由此可见,第一个匹配失败的时候S[i]=’c’,主串指针需要+2才有可能在下一次匹配成功,同理第二次匹配失败的时候,S[i]=’a’,主串指针需要+3直接跳过’a’才能下一次匹本成功。
对于S[i]字符,有256种可能,所以需要对于模式串建立一张长度为256的坏字符表,其中当P中没出现的字符,表值为plen,如果出现了,则设置为最近的一个对齐的值。具体算法比较简单如下:
这个时候整个算法的匹配算法该是怎么样的呢,是将上面的search_reverse函数中的s_idx+=(plen-p_idx)+1改成s_idx+= shift[(unsigned char)patn[p_idx]] +1吗? 不是的,代码给出如下,具体原因读者可自行分析。
- /*
- 函数:void BuildBadCharacterShift(char *, int, int*)
- 目的:根据好后缀规则做预处理,建立一张好后缀表
- 参数:
- pattern => 模式串P
- plen => 模式串P长度
- shift => 存放坏字符规则表,长度为的int数组
- 返回:void
- */
- void BuildBadCharacterShift(char const* pattern, int plen, int* shift)
- {
- for( int i = 0; i < 256; i++ )
- *(shift+i) = plen;
- while ( plen >0 )
- {
- *(shift+(unsigned char)*pattern++) = --plen;
- }
- }
- /*! int search_badcharacter(char const*, int, char const*, int)
- */bref 查找出模式串patn在主串src中第一次出现的位置
- */return patn在src中出现的位置,当src中并没有patn时,返回-1
- */
- int search_badcharacter(char const* src, int slen, char const* patn, int plen, int* shift)
- {
- int s_idx = plen, p_idx;
- int skip_stride;
- if (plen == 0)
- return -1;
- while (s_idx <= slen)//计算字符串是否匹配到了尽头
- {
- p_idx = plen;
- while (src[--s_idx] == patn[--p_idx])//开始匹配
- {
- //if (s_idx < 0)
- //Return -1;
- if (p_idx == 0)
- {
- return s_idx;
- }
- }
- skip_stride = shift[(unsigned char)src[s_idx]];
- s_idx += (skip_stride>plen-p_idx ? skip_stride: plen-p_idx)+1;
- }
- return -1;
- }
在讲最好后缀规则之前,我们先回顾一下本部分第1小节中所举的一个简单后比对算法的例子:
上面倒数第二步匹配是没必要的。为什么呢?在倒数第三步匹配过程中,已有最后两个字符与模式串P中匹配,而模式串中有前两个与后两个字符相同的,所以可以直接在接下来将P中的前两个与主串中匹配过的’ab’对齐,做为下一次匹配的开始。
其实思路与本文第一部分讲过的KMP算法差不多,也是利用主串与模式串已匹配成功的部分来找一个合适的位置方便下一次最有效的匹配。只是这里是需要寻找一个位置,让已匹配过的后缀与模式串中从后往前最近的一个相同的子串对齐。(理解这句话就理解了BM算法的原理)这里就不做数学描述了。
ok,主体思想有了,怎么具体点呢?下面,直接再给一个例子,说明这种匹配过程。看下图吧。
由图可以goodsuffixshift[5] = 5
求解最好后缀数组是BM算法之所以难的根本,所以建议多花时间理清思路。网上有很多方法,我也试过两个,一经测试,很多都不算准确,最好后缀码的求解不像KMP的“最好前缀数组”那样可以用递推的方式求解,而是有很多细节。
代码如下:
- /*
- 函数:void BuildGoodSuffixShift(char *, int, int*)
- 目的:根据最好后缀规则做预处理,建立一张好后缀表
- 参数:
- pattern => 模式串P
- plen => 模式串P长度
- shift => 存放最好后缀表数组
- 返回:void
- */
- void BuildGoodSuffixShift(char const* pattern, int plen, int* shift)
- {
- shift[plen-1] = 1; // 右移动一位
- char end_val = pattern[plen-1];
- char const* p_prev, const* p_next, const* p_temp;
- char const* p_now = pattern + plen - 2; // 当前配匹不相符字符,求其对应的shift
- bool isgoodsuffixfind = false; // 指示是否找到了最好后缀子串,修正shift值
- for( int i = plen -2; i >=0; --i, --p_now)
- {
- p_temp = pattern + plen -1;
- isgoodsuffixfind = false;
- while ( true )
- {
- while (p_temp >= pattern && *p_temp-- != end_val); // 从p_temp从右往左寻找和end_val相同的字符子串
- p_prev = p_temp; // 指向与end_val相同的字符的前一个
- p_next = pattern + plen -2; // 指向end_val的前一个
- // 开始向前匹配有以下三种情况
- //第一:p_prev已经指向pattern的前方,即没有找到可以满足条件的最好后缀子串
- //第二:向前匹配最好后缀子串的时候,p_next开始的子串先到达目的地p_now,
- //需要判断p_next与p_prev是否相等,如果相等,则继续住前找最好后缀子串
- //第三:向前匹配最好后缀子串的时候,p_prev开始的子串先到达端点pattern, 这个可以算是最好的子串
- if( p_prev < pattern && *(p_temp+1) != end_val ) // 没有找到与end_val相同字符
- break;
- bool match_flag = true; //连续匹配失败标志
- while( p_prev >= pattern && p_next > p_now )
- {
- if( *p_prev --!= *p_next-- )
- {
- match_flag = false; //匹配失败
- break;
- }
- }
- if( !match_flag )
- continue; //继续向前寻找最好后缀子串
- else
- {
- //匹配没有问题, 是边界问题
- if( p_prev < pattern || *p_prev != *p_next)
- {
- // 找到最好后缀子串
- isgoodsuffixfind = true;
- break;
- }
- // *p_prev == * p_next 则继续向前找
- }
- }
- shift[i] = plen - i + p_next - p_prev;
- if( isgoodsuffixfind )
- shift[i]--; // 如果找到最好后缀码,则对齐,需减修正
- }
- }
注:代码里求得到的goodsuffixshift值与上述图解中有点不同,这也是我看网上代码时做的一个小的改进。请注意。另外,如上述代码的注释里所述,开始向前匹配有以下三种情况:
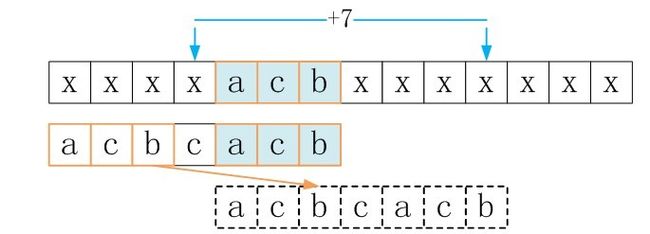
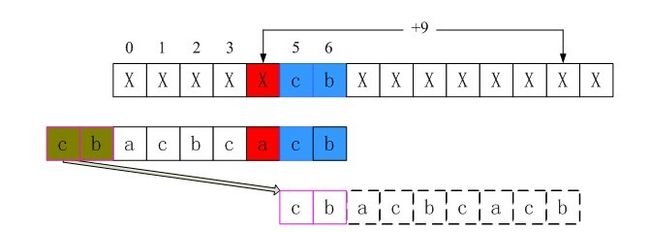
从图中可以看出,在模式串P中,P[2]=P[6]但P[1]也等于P[5],所以如果只移5位让P[2]与S[6]对齐是没必要的,因为P[1]不可能与S[5]相等(如红体字符表示),对于这种情况,P[2]=P[6]就不算最好后缀码了,所以应该直接将整个P滑过S[6],所以goodsuffixshift[5]=8而不是5。也就是说,在匹配过程中已经得出P[1]是不可能等于S[5]的,所以,就算为了达到P[2]与S[6]匹配的效果,让模式串P右移5位,但在P[1]处与S[5]处还是会导致匹配失败。所以,必定会匹配失败的事,我们又何必多次一举呢?
那么,我们到底该怎么做呢?如果我现在直接给出代码的话,可能比较难懂,为了进一步说明,以下图解是将BM算法的好后缀表数组shift(不匹配时直接跳转长度数组)的求解过程。其中第一行为src数组,第二行为patn数组,第三行为匹配失败时下一次匹配时的patn数组(粉色框的元素实际不存在)。
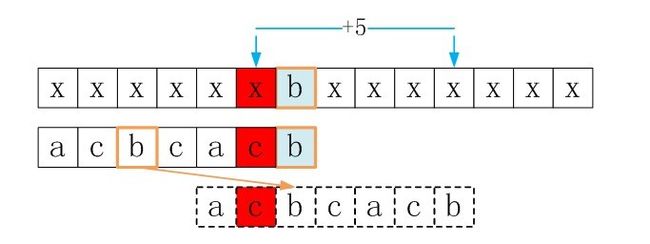
ok,现在咱们定位于P[5]处,当i = 5时src[5] != patn[5],p_now指向patn[5],而p_prev指向patn[1],即情况二。由于此时*p_prev == *p_now,则继续往前找最好后缀子串。循环直到p_prev指向patn[0]的前一个位置(实际不存在,为了好理解加上去的)。此时p_prev指向patn[0]的前方,即情况一。此时条件p_prev < pattern && *(p_temp+1) != end_val满足,所以跳出循环。计算shift[5]= plen - i + p_next - p_prev =8(实际上是第三行的长度)。
i= 4时,src[4] != patn[4],此时p_prev指向patn[0],p_now指向patn[4],即情况二。由于此时*p_prev == *p_now,则继续往前找最好后缀子串。循环直到p_prev指向patn[0]的前一个位置。此时p_prev指向patn[0]的前方,即情况一。此时条件p_prev < pattern && *(p_temp+1) != end_val满足,所以跳出循环。计算shift[4]= plen - i + p_next - p_prev =9(实际上是第三行的长度)。
同样的过程可以得到,i = 3时shift[3]也为第三行的长度7。
同样的过程可以得到,i = 2时shift[2]也为第三行的长度8。
5、i = 1时不匹配的情况
同样的过程可以得到,i = 1时shift[1]也为第三行的长度9。
6、i = 0时不匹配的情况
同样的过程可以得到,i = 0时shift[0]也为第三行的长度10。
计算好后缀表数组后,这种情况下的字模式匹配算法为:
- /*! int search_goodsuffix(char const*, int, char const*, int)
- */bref 查找出模式串patn在主串src中第一次出现的位置
- */return patn在src中出现的位置,当src中并没有patn时,返回-1
- */
- int search_goodsuffix(char const* src, int slen, char const* patn, int plen, int* shift)
- {
- int s_idx = plen, p_idx;
- int skip_stride;
- if (plen == 0)
- return -1;
- while (s_idx <= slen)//计算字符串是否匹配到了尽头
- {
- p_idx = plen;
- while (src[--s_idx] == patn[--p_idx])//开始匹配
- {
- //if (s_idx < 0)
- //return -1;
- if (p_idx == 0)
- {
- return s_idx;
- }
- }
- skip_stride = shift[p_idx];
- s_idx += skip_stride +1;
- }
- return -1;
- }
4、BM算法
有了前面的三个步骤的算法的基础,BM算法就比较容易理解了,其实BM算法就是将坏字符规则与最好后缀规则的综合具体代码如下,相信一看就会明白。
- /*
- 函数:int* BMSearch(char *, int , char *, int, int *, int *)
- 目的:判断文本串T中是否包含模式串P
- 参数:
- src => 文本串T
- slen => 文本串T长度
- ptrn => 模式串P
- pLen => 模式串P长度
- bad_shift => 坏字符表
- good_shift => 最好后缀表
- 返回:
- int - 1表示匹配失败,否则反回
- */
- int BMSearch(char const*src, int slen, char const*ptrn, int plen, int const*bad_shift, int const*good_shift)
- {
- int s_idx = plen;
- if (plen == 0)
- return 1;
- while (s_idx <= slen)//计算字符串是否匹配到了尽头
- {
- int p_idx = plen, bad_stride, good_stride;
- while (src[--s_idx] == ptrn[--p_idx])//开始匹配
- {
- //if (s_idx < 0)
- //return -1;
- if (p_idx == 0)
- {
- return s_idx;
- }
- }
- // 当匹配失败的时候,向前滑动
- bad_stride = bad_shift[(unsigned char)src[s_idx]]; //根据坏字符规则计算跳跃的距离
- good_stride = good_shift[p_idx]; //根据好后缀规则计算跳跃的距离
- s_idx += ((good_stride > bad_stride) ? good_stride : bad_stride )+1;//取大者
- }
- return -1;
- }