1066. Root of AVL Tree (25)
题目链接：http://www.patest.cn/contests/pat-a-practise/1066
题目：
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
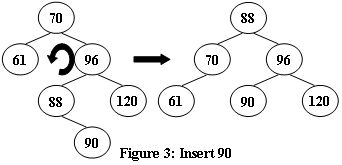
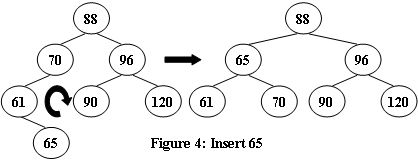
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (<=20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print ythe root of the resulting AVL tree in one line.
Sample Input 1:5 88 70 61 96 120Sample Output 1:
70Sample Input 2:
7 88 70 61 96 120 90 65Sample Output 2:
88
分析：
平衡二叉树的插入
参考资料：
http://www.cppblog.com/cxiaojia/archive/2013/07/22/187776.html平衡二叉树的介绍，用模版写的
http://blog.csdn.net/realxuejin/article/details/12871919针对PAT66的代码
//左左情况下的旋转
template<class T>
void AVLTree<T>::SingRotateLeft(TreeNode<T>* &k2)
{
TreeNode<T>* k1;
k1=k2->lson;
k2->lson=k1->rson;
k1->rson=k2;
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->lson),k2->hgt)+1;
}
//右右情况下的旋转
template<class T>
void AVLTree<T>::SingRotateRight(TreeNode<T>* &k2)
{
TreeNode<T>* k1;
k1=k2->rson;
k2->rson=k1->lson;
k1->lson=k2;
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->rson),k2->hgt)+1;
}
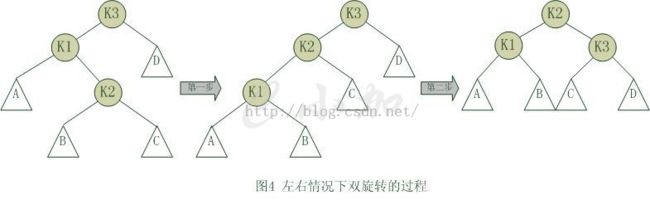
//左右情况的旋转
template<class T>
void AVLTree<T>::DoubleRotateLR(TreeNode<T>* &k3)
{
SingRotateRight(k3->lson);
SingRotateLeft(k3);
}
//右左情况的旋转
template<class T>
void AVLTree<T>::DoubleRotateRL(TreeNode<T>* &k3)
{
SingRotateLeft(k3->rson);
SingRotateRight(k3);
}插入：
//插入
template<class T>
void AVLTree<T>::insertpri(TreeNode<T>* &node,T x)
{
if(node==NULL)//如果节点为空,就在此节点处加入x信息
{
node=new TreeNode<T>();
node->data=x;
return;
}
if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中插入x
{
insertpri(node->lson,x);
if(2==height(node->lson)-height(node->rson))
if(x<node->lson->data)
SingRotateLeft(node);
else
DoubleRotateLR(node);
}
else if(node->data<x)//如果x大于节点的值,就继续在节点的右子树中插入x
{
insertpri(node->rson,x);
if(2==height(node->rson)-height(node->lson))//如果高度之差为2的话就失去了平衡,需要旋转
if(x>node->rson->data)
SingRotateRight(node);
else
DoubleRotateRL(node);
}
else ++(node->freq);//如果相等,就把频率加1
node->hgt=Max(height(node->lson),height(node->rson));
}
//插入接口
template<class T>
void AVLTree<T>::insert(T x)
{
insertpri(root,x);
}
AC代码：
#include<iostream>
#include<cstdio>
#include<cmath> //abs需要
using namespace std;
struct Node{
int value;
Node *lchild;
Node *rchild;
int height;
Node(int v) :value(v), lchild(NULL), rchild(NULL), height(0){}
Node() :lchild(NULL), rchild(NULL){}
};
int getHeight(Node *t){
if (t == NULL)return -1;
else return t->height;
}
int max(int a, int b){
return a > b ? a : b;
}
Node *SingleRotateLeft(Node *k2){//左左的情况
Node *k1;
k1 = k2->lchild;
k2->lchild = k1->rchild;
k1->rchild = k2;
k2->height = max(getHeight(k2->lchild), getHeight(k2->rchild)) + 1;
k1->height = max(getHeight(k1->lchild), getHeight(k1->rchild)) + 1;
return k1;
}
Node *SingleRotateRight(Node *k2){//右右的情况
Node *k1;
k1 = k2->rchild;
k2->rchild = k1->lchild;
k1->lchild = k2;
k2->height = max(getHeight(k2->lchild), getHeight(k2->rchild)) + 1;
k1->height = max(getHeight(k1->lchild), getHeight(k1->rchild)) + 1;
return k1;
}
Node *DoubleRotateLR(Node *k3){//左右的情况
k3->lchild = SingleRotateRight(k3->lchild);
return SingleRotateLeft(k3);
}
Node *DoubleRotateRL(Node *k3){//右左的情况
k3->rchild = SingleRotateLeft(k3->rchild);
return SingleRotateRight(k3);
}
bool isBalanced(Node *left, Node *right){
return abs(getHeight(left) - getHeight(right)) < 2;
}
Node *insert(int v, Node *root){
if (root == NULL){
root = new Node(v);
return root;
}
else if (v > root->value){
root->rchild = insert(v, root->rchild);
if (!isBalanced(root->lchild, root->rchild)){
if (v > root->rchild->value)
root = SingleRotateRight(root);
else
root = DoubleRotateRL(root);
}
}
else{
root->lchild = insert(v, root->lchild);
if (!isBalanced(root->lchild, root->rchild)){
if (v < root->lchild->value)
root = SingleRotateLeft(root);
else
root = DoubleRotateLR(root);
}
}
root->height = max(getHeight(root->lchild), getHeight(root->rchild)) + 1;
return root;
}
int main(void){
freopen("F://Temp/input.txt", "r", stdin);
int n;
scanf("%d", &n);
Node *root = NULL;
int tmp;
for (int i = 0; i < n; i++){
scanf("%d", &tmp);
root = insert(tmp, root);
}
printf("%d\n", root->value);
return 0;
}
截图：
——Apie陈小旭