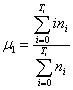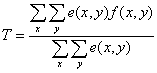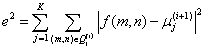图像分割理论

在对图像的研究和应用中，人们往往仅对图像中的某些部分感兴趣，这些部分一般称为目标或前景。为了辨识和分析目标，需要将有关区域分离提取出来，在次基础上对目标进一步利用，如进行特征提取和测量。图像分割就是指把图像分成各具特性区域并提取出感兴趣目标的技术过程。其中边缘检测就是图像分割的一部分。

Hough变换：

Hough变换是图像处理中从图像中识别几何形状的基本方法之一。Hought变换的基本原理在于利用点到线的对偶性，将原始图像空间中给定的曲线通过曲线表达形式变为参数空间中的一个点。这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题，也即把检测整体特性转化为检测局部特性，比如直线、椭圆、圆、弧线等。

Hough变换原理：

在图像空间X-Y中的一点，经过点-正弦曲线对偶的Hough变换：

在参数空间中变为一条正弦曲线，其中取（）。可以证明，图像空间X-Y中直线上的点经过Hough变换后，它们的正弦曲线在参数空间中有一个公共交点。也就是说，参数空间中的一点，对应于图像空间X-Y中的一条直线，而且它们是一一对应的。

因此，为了检测出图像空间X-Y中由点所构成的直线，可以将参数空间量化成许多小格。根据图像空间X-Y中每个点的坐标。在内以小格的步长计算各个值，所得值落在某个小格内，便使该小格的累加计数器加1.当图像空间中全部的点都变换后，对小格进行检验，计数值最大的小格，其值对应于图像空间中所求直线。

参数空间中的、与图像空间中直线的斜率k和截距b的关系为：

阈值法：

阈值分割法是一种基于区域的图像分割技术，其基本原理是：通过设定不同的特征阈值，把图像像素点分为若干类。设原始图像为，按照一定的准则在该图像中找到特征值T，将图像分割为两个部分，分割后的图像为：

若取为黑，为白，即为图像的二值化。

阈值分割法是一种最常用也是最简单的图像分割方法，它特别适用于目标和背景占据不同灰度级范围的图像。阈值分割法一般分为人工选择和自动选择法，人工法就是结合直方图人为地选择阈值。在这主要介绍自动阈值选择法，其中包括：迭代法、Otsu法、一维最大熵法、二维最大熵法、简单统计法。

迭代法

迭代法的基本思想是：开始时选择一个阈值作为初始化估计值，然后按照某种车辆通过迭代不断地改变这一估值，直到满足给定的准则为止，其具体步骤如下。

（1）在一幅灰度范围为[0,L-1]的图像中，选择图像灰度的中值作为初始化阈值，其中图像中对应灰度级i的像素为。

（2）利用阈值T把图像分割成两个区域：和，用下式计算区域和的平均灰度值和。

         ，   

（3）计算出和后，用下式计算出新的阈值。

        

（4）重复步骤（2）~（3），直到和的差小于某个给定值为止。

Otsu法

Otsu法是一种使类间方差最大的阈值确定法，所以也称为最大类间方差法。该方法具有简单、处理速度快等特点，是一种常用的阈值选取方法。其基本思想是：把图像中的像素按灰度值用阈值T分成 两类和，由灰度值在之间的像素组成，由灰度值在之间的像素组成，按下式计算两类之间的类间方差：

式中，为中包含的像素数，为中包含的像素数，为中所有像素的平均灰度值，为中所有像素的平均灰度值。让在范围依次取值，让最大的值即为Otsu法的最佳阈值。

一维最大熵法

熵是平均信息量的表征。把信息熵的概念应用于图像阈值分割的基本思想是：利用图像的灰度分布密度函数定义图像的信息熵，根据假设的不同或视角的不同提出不同的熵准则，最后通过优化该准则得到熵值。其中一维最大熵求阈值的方法如下。

在一幅灰度范围为的图像中，熵函数定义为：

式中：

，   ， 

为灰度级出现的概率。

当熵函数取得最大值时，对应的灰度值就是所求的最佳熵值。

二维最大熵法

由于灰度一维最大熵是基于图像原始直方图的，它仅仅利用了点灰度信息而未充分利用图像的空间信息，而二维最大熵综合利用了点灰度特征和区域灰度特征，从而较好地表征了图像的信息。它的基本方法是：以原始灰度图像（个灰度级）中各像素及其4邻域的4个像素为一个区域，计算出区域灰度均值图像，这样原始图像中的每一个像素都对应于一个点灰度-区域灰度均值时，设为图像中点灰度为及其区域灰度均值为的像素点数，为点灰度-区域灰度均值对发生的概率，则：

其中为图像的大小。

则二维最大熵的判别函数为：

使为最大的阈值和即为所求阈值。其中：

                                 

                  

                  

简单统计法

简单统计法是一种基于简单的图像统计的阈值选取方法。使用该方法，能直接计算一幅图像为的阈值。该方法的计算公式为：

其中：

特征空间聚类法：

特征空间聚类法即根据某些特征将目标点划分到相应的类别中，这种方法是一种比较简单有效的图像分割方法。典型的特征空间聚类方法包括：K-均值聚类法、ISODATA法、模糊C-均值法等。

K-均值聚类法原理

K-均值聚类法可以将一幅图像分割成个区域。设代表数字图像像素的坐标，代表像素的灰度，则K-均值法的最小化指标为：

式中：表示图像中有个区域，表示在第次迭代后图像中第个区域，表示次迭代后第个区域的平均值。上式实际上给出了每个像素与其对应区域均值的距离和。

K-均值聚类算法的具体步骤如下：

（1）任意选个初始类均值，。

（2）在第次迭代时，根据下述距离准则将每个像素都赋给类（区域）之一：

               若

          即将每个像素赋给均值离开它最近的类。

（3）对每个类，更新该类的均值：

          

          式中是更新后的类中的像素个数。

（4）如果对所有的类，有，则算法收敛，结束；否则退回步骤（2）继续下一迭代。

ISODATA聚类法原理

ISODATA聚类方法是在K-均值算法上发展起来的，它是在没有先验知识的情况下进行的一种无监督分类。首先，它选择若干样本作为聚类中心，再按照某种聚类准则，使其余样归入最近的聚类中心，得到初始聚类；然后判断初始聚类结果是否合理，若不合理则按照特定规则将聚类集合进行分裂或合并，以获得新的聚类中心，再判断聚类结果是否符合要求。如此反复迭代，直到聚类划分符合要求为止。

为了简化程序，在此选择的初始聚类数目远远大于预期聚类数目，因此只需考虑合并聚类，而不会出现分裂聚类这种情况。具体的步骤如下：

（1）设置初始聚类数目为预期聚类数目的两倍，并任意选取个初始聚类的均值；

（2）求各个样本到所有聚类中心的距离，按照与聚类中心距离最小的原则将各样本归入最近的聚类；

（3）更新各聚类均值；如果某聚类内的样本数目为零，则抛弃该聚类，并使聚类数目；

（4）计算全部聚类均值之间的距离，找到其最小距离。设聚类和聚类之间的距离最小，则将两个类合并，合并后的聚类均值为：

          

         式中：、和分别为合并前聚类和聚类的均值，及其合并后聚类的均值，和为聚类和聚类内的样本数目。合并后聚类的样本数目为和之和，此时聚类数目；

（5）如果不大于，则结束；否则退回步骤（2）继续下一次迭代。

松弛迭代法

松弛迭代分割法是以像素为操作对象，借助迭代逐步确定各像素的归类。每次迭代中，需要用到称为相容性的准则。它的基本思想是图像中每一个像素的归属不仅应该由其本身来决定，而且应该受到它的邻域像素的影响。

松弛迭代分割法可以用以下3个步骤来完成。

（1）随机初始化标记

          设图像的大小为，像素为，用阈值法将图像分为个类；第类的均值和方差分别为和。因为像素点和第类的马氏距离为：

          

          则初始化概率为：

          

（2）规则更新

          对于类和类，相容性矩阵R定义为：

          

          如果用表示类对点的相容性因素，用表示点的邻域，则：

          

          当只考察8点邻域时，则。在第步的概率矢量可用下式计算：

          

（3）迭代终止

         松弛迭代是一种像素标记方法，所以可设定一个量（如百分比）来确定迭代是否达到预期目标，并在达到时认为迭代收敛，终止算法。