每天学一点算法-Dijkstra算法

Dijkstra算法

定义

戴克斯特拉算法（Dijkstra’s algorithm）是由荷兰计算机科学家艾兹赫尔·戴克斯特拉提出。迪科斯彻算法使用了广度优先搜索解决非负权有向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

　　该算法的输入包含了一个有权重的有向图 G，以及G中的一个来源顶点 S。我们以 V 表示 G 中所有顶点的集合。每一个图中的边，都是两个顶点所形成的有序元素对。(u, v) 表示从顶点 u 到 v 有路径相连。我们以 E 表示G中所有边的集合，而边的权重则由权重函数 w: E → [0, ∞] 定义。因此，w(u, v) 就是从顶点 u 到顶点 v 的非负权重（weight）。边的权重可以想像成两个顶点之间的距离。任两点间路径的权重，就是该路径上所有边的权重总和。已知有 V 中有顶点 s 及 t，Dijkstra 算法可以找到 s 到 t的最低权重路径(例如，最短路径)。这个算法也可以在一个图中，找到从一个顶点 s 到任何其他顶点的最短路径。对于不含负权的有向图，Dijkstra 算法是目前已知的最快的单源最短路径算法。

步骤

1.初始时令 S={V0},T={其余顶点}，T中顶点对应的距离值

　　若存在<V0,Vi>，d(V0,Vi)为<V0,Vi>弧上的权值

　　若不存在<V0,Vi>，d(V0,Vi)为∞

2.  从T中选取一个其距离值为最小的顶点W且不在S中，加入S

3.  对其余T中顶点的距离值进行修改：若加进W作中间顶点，从 V0 到 Vi 的距离值缩短，则修改此距离值

　　重复上述步骤2、3，直到S中包含所有顶点，即W=Vi 为止

理解

花了宝贵的一下午研究了算法，遍历所需。总结如下：

时间复杂度：执行算法所需要的计算工作量

空间复杂度：执行算法所需要的内存空间

T(n)：时间复杂度,大O标识。

  时间复杂度T(n)按数量级递增顺序为：

常数阶		对数阶	线性阶	线性对数阶	平方阶	立方阶	……	K次方阶	指数阶
O(1)		O(log2n)	O(n)	O(nlog2n)	O(n2)	O(n3)		O(nk)	O(2n)

复杂度低 ---->---->---->---->---->---->---->---->---->---->---->---->----> 复杂度高

S(n)：空间复杂度。大O标识，空间的复杂度要上机实际运行才能知道。

有向图非负权最短路径算法，时间复杂度O（n的平方）。

1.有2个保存顶点的数组，S和U。S保存已经已经获得与起始点最短路径的顶点。U中保存剩下的没有获得最短距离的顶点。

2.遍历开始：将起始点从U移到S中，然后遍历U中顶点到起始点的距离，取最小的距离的顶点移到S中。然后以该顶点为中间点开始遍历，意思就是：起始点A，然后发现了A->C的距离是A可到达的所有顶点中最小的距离，然后把C从U中移到S中，然后下一次遍历就要以C为中间点A-C->莫个跟C邻近的点。

3.计算剩下的顶点距起始点距离，如果存在S中直接可以到达的，比如A可以到达B，然后它的距离又比A-C-B（且是唯一一条从C为中间点）的距离要近，那么A-B的最短距离要更新为a-b的权值，而不是A-C-B的权值。

而在程序中实现的时候是通过2维数组的形式保存有向图的信息。例如A-C-B的保存形式为,权值为2-1

int[][]  a = {{0,max,2}，{max,0,max},{max,1,0}};

数组中的第一个元素表示A顶点，和自己的距离为0。与B因为不临近，所以为无穷大。与C的距离为2

第二个元素表示B元素与A不临近，与自己为0。与C不临近。

第三个元素表示C与A不临近，与B为1的距离，与自己为0。

然后我们将该数组做dijkstra遍历。我们默认以A为标准点，也就是以A为起始点。

首先第一步将数组a的第一个元素保存到map中。保存已经获得最近距离的点，和该距离的数值。map<索引，值>

刚开始map中的数值是这样的<0,0><1,max><2,2>代表的就是各点与A的距离。然后我们会取距离最小的点，也就是起始点本身（距离为0），加入到保存已得到最低距离的数组S中（List<interger> S=new ArrayList(interger)）。至于第一步中的U数组，在编程中并没有具体，而是保存在原始的map中。

然后进入第三步的遍历的状态，因为第二步的转移过程已经完成。第三步就是判断A的邻近点是否有比A到本身距离低的。（当然这是不可能的）它会遍历二维数组的其他元素，将里面的权值调出来和当前顶点与起始点的距离相加看是否还小于当前的距离。如果成立，那么该节点的最低距离就会变为该值。

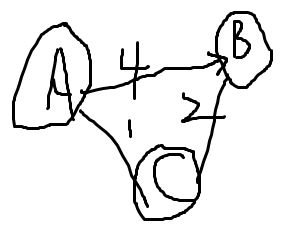
抛开上面A-C-B的限制，为了讲的清楚，我假设如下图：

刚开始，我遍历A-C，A-B。然后A-C的距离近，我把C添加到S中。然后以C为中间节点A-C-B=3。发现比A-B的距离近，这时候我就更新map里的值啦。<1,4>就要变为<1,3>。

将B添加到S中，以A-B遍历剩下的顶点。

OY。爽！

时间复杂度

O(n^2)

摘录别人的代码，帮助分析：

代码

package com.spreadtrum.apptraverse.test;

import java.util.HashMap;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Map.Entry;
import java.util.Set;

public class ShortestPath {
	private static final int minDis = 0;
	private static final int maxDis = Integer.MAX_VALUE;
	// 图的邻接矩阵
	int[][] matrix;
	// 起始点
	int startIndex;
	// 用来存放起始点到其它点当前的距离
	HashMap<Integer, Integer> distanceMap = new HashMap<Integer, Integer>();
	// 用来存放已经找到最短路径的点的集合
	Set<Integer> findedSet = new HashSet<Integer>();

	public ShortestPath(int[][] matrix, int start) {
		this.matrix = matrix;
		this.startIndex = start;
		// findedSet.add(startIndex);
		find();
		printDistance();
	}

	public void find() {
		// 用start相邻的点初始化distanceMap
		for (int i = 0; i < matrix.length; i++) {
			// if (matrix[startIndex][i] != maxDis)
			//i代表第几个点，第二个参数代表到起始点的距离，第i个点到起始点的距离为matrix[startIndex][i]的值，也就是二维数组中一行里的数据。
			distanceMap.put(i, matrix[startIndex][i]);
		}

		while (findedSet.size() != matrix.length) {
			//剩余节点中距离起始点最近的距离的点
			int currentMinIndex = currentMinIndex();
			// 用此结点更新其它结点的距离
			for (int i = 0; i < matrix.length; i++) {
				//S数组中没有该索引点，必须是当前点的邻近点，当前距离+当前点与相邻点的距离相加<i索引点的距离。
				if (!findedSet.contains(i) && matrix[currentMinIndex][i] != maxDis
						&& matrix[currentMinIndex][i] + distanceMap.get(currentMinIndex) < distanceMap.get(i))
					distanceMap.put(i, matrix[currentMinIndex][i] + distanceMap.get(currentMinIndex));
			}
			// 放入findedset
			findedSet.add(currentMinIndex);
		}
	}

	// 打印从起始点到所有点的最短距离
	public void printDistance() {
		Iterator<Entry<Integer, Integer>> it = distanceMap.entrySet().iterator();
		int min = Integer.MIN_VALUE;
		int minIndex = -1;
		while (it.hasNext()) {
			Entry<Integer, Integer> entry = it.next();
			System.out.println(startIndex + "---->" + entry.getKey() + ":" + entry.getValue());
		}
	}

	// 返回当前最小距离的点(必须不包含在findedSet中)
	private int currentMinIndex() {
		Iterator<Entry<Integer, Integer>> it = distanceMap.entrySet().iterator();
		int min = Integer.MAX_VALUE;
		int minIndex = -1;
		while (it.hasNext()) {
			Entry<Integer, Integer> entry = it.next();
			System.out.println("距起始点距离" + entry.getValue());
			if (!findedSet.contains(entry.getKey()) && entry.getValue() < min) {
				min = entry.getValue();
				minIndex = entry.getKey();
			}
		}
		System.out.println("=====");
		return minIndex;
	}

	public static void main(String[] args) {
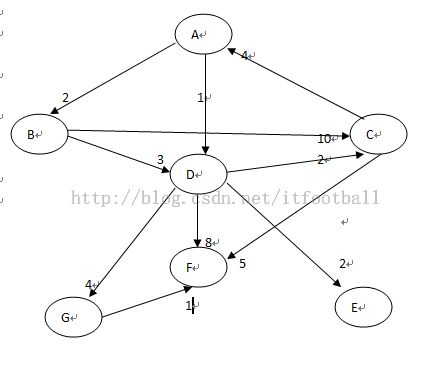
		int[][] inputMatrix = new int[][] { { minDis, 2, maxDis, 1, maxDis, maxDis, maxDis },
				{ maxDis, minDis, maxDis, 3, 10, maxDis, maxDis }, { 4, maxDis, minDis, maxDis, maxDis, 5, maxDis },
				{ maxDis, maxDis, 2, minDis, 2, 8, 4 }, { maxDis, maxDis, maxDis, maxDis, minDis, maxDis, 6 },
				{ maxDis, maxDis, maxDis, maxDis, maxDis, minDis, maxDis },
				{ maxDis, maxDis, maxDis, maxDis, maxDis, 1, minDis } };
		ShortestPath path = new ShortestPath(inputMatrix, 0);
		/*path.find();
		path.printDistance();*/

	}
}