算法和数据结构面试题(24)-几个数的和等于m

题目

输入两个整数n 和m，从数列1，2，3.......n 中随意取几个数,
使其和等于m ,要求将其中所有的可能组合列出来.

解题思路

有没有和之前做过的一题有点类似。

算法与数据结构面试题(14)-在数组中查找2个数的和为已知数

但是这一题不只是求出2个数之和，任意个数之和等与m。动态规划法-背包问题：

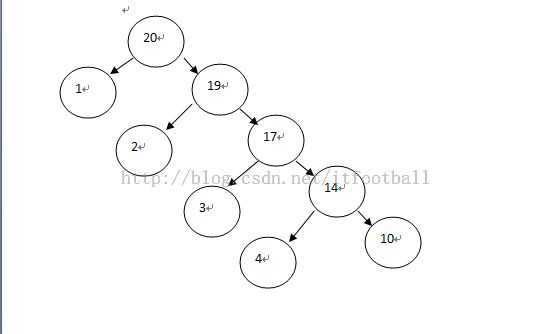
例如上图，比如我们要求20。那么它可以是1+19。这个时候我们就将19作为目标，再遍历，因为1已经被用过了，所以从2开始，19 = 2+17。依次类推

符合20的组合为：

1，19

1，2，17

1，2，3，14

1，2，3，4，10

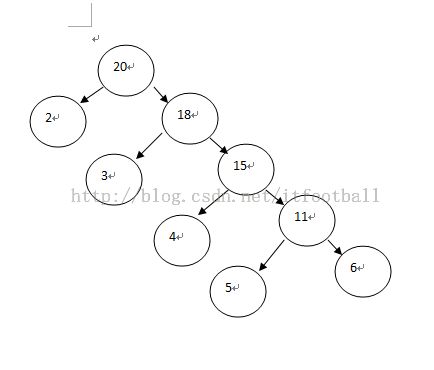
再以2开始

符合条件的是

2，18

2，3，15

2，3，4，11

2，3，4，5，6

为了防止有重复的，我们用一个hashset来保存所有的可选元素，被选择以后，就要从这个里面删除。放到另一个list集合，该list代表已选的点。这样当有符合条件的组合的时候，我们就将该组合输出。

代码

/**
 * 
 * @author: hui.qian Created on 2014年12月31日 下午5:01:33 Description: 输入两个整数n
 *          和m，从数列1，2，3.......n 中随意取几个数, 使其和等于m ,要求将其中所有的可能组合列出来.
 */
public class Problem21 {
    Queue<String> queue = new LinkedList<String>();
    Set<Integer> total = new HashSet<Integer>();
    List<Integer> list = new ArrayList<Integer>();

    // 递归
    public void f(int n, int m) {
        // m=1或者m=2情况,都没有2个数相加的情况.n小于2的时候,就不符合相加的条件,至少需要2个数吧。
        if (m < 3 || n < 2) {
            return;
        }
        for (int i = n; i > 0; i--) {
            int m1 = m - i;
            // 阻止重复的方式。(1,9=9,1)
            if (m1 > i || !total.contains(m1)) {
                continue;
            }
            // 为当前分支的数组做一次调整
            initData(list, i);

            if (!list.contains(m1)) {
                // 符合要求的放入打印队列中
                if (!list.isEmpty()) {
                    addListToPrintQueue(list);
                }
                addToPrintQueue(m1);
                addTabToQueue();
            }
            // 然后再从剩下的数中找出和等于m1
            f(m1, m1);

            // 分支结束后,要把状态恢复到最初的状态
            releaseData(list, i);
        }

    }

    // 还原到最初的状态
    private void releaseData(List<Integer> list, int i) {
        list.remove((Integer) i);
        total.add(i);
    }

    // 调整2个集合中的数字,就是将total中的数字移到list中
    private void initData(List<Integer> list, int i) {
        // 保存最大的数
        list.add(i);
        // 从待选择数据结合中移除该数
        total.remove((Integer) i);
    }

    private void parseToList(int n) {
        for (int i = 1; i <= n; i++) {
            total.add(i);
        }
    }

    // 将list表中的所有数据添加到打印队列中
    private void addListToPrintQueue(List<Integer> list) {
        for (Integer in : list) {
            addToPrintQueue(in);
        }

    }

    // 将某个数添加到打印队列中
    private void addToPrintQueue(int a) {
        queue.add(a + "");
    }

    // 将换行符添加到打印队列中
    private void addTabToQueue() {
        queue.add("\n");
    }

    private void printQueue() {
        while (!queue.isEmpty()) {
            System.out.print(queue.poll());
        }
    }

    public static void main(String[] args) {
        Problem21 problem = new Problem21();

        int n = 20;
        int m = 21;
        problem.parseToList(n);
        // 如果m小于n，那么大于n的部分肯定不会被取到，只会从m的下一个开始取，增加一点效率
        // m是否在1-n范围内。如果在的话，首先要m一个数就符合要求。
        // 获取所有组合
        problem.f(n, m);
        // 打印所有组合
        problem.printQueue();
    }

}

n = 20,m = 21的时候输出。

20 1 
 19 2 
 18 3 
 18 2 1 
 17 4 
 17 3 1 
 16 5 
 16 4 1 
 16 3 2 
 15 6 

n=20,m=8的时候

7 1 
6 2 
5 3 
5 2 1 
4 3 1