关于大整数包的设计！
C/C++中的int类型能表示的范围是-2E31－2E31–1。unsigned类型能表示的范围是0－2E32–1，即 0－4294967295。所以，int和unsigned类型变量，都不能保存超过10位的整数。有时我们需要参与运算的数，可能会远远不止10 位，例如，可能需要保留小数点后面100位（比如求π的值），那么，即便使用能表示很大数值范围的double变量，但是由于double变量只有64位，所以还是不可能达到精确到小数点后面100位这样的精度。
double变量的精度也不足以表示一个100位的整数。一般我们称这种基本数据类型无法表示的整数为大整数。如何表示和存放大整数呢？基本的思想就是：用数组存放和表示大整数。一个数组元素，存放大整数中的一位。
2.开一个比较大的整型数组，数组的元素代表数组的某一位或者某几位。
3.通过对数组元素的运算模拟大数的运算。
大整数乘法
再下来算4×3。此处4×3 的结果代表12 个100，因此要 c[2]+= 12，变为：
最后算 4×8。此处4×8 的结果代表 32 个1000，因此要 c[3]+= 32，变为：
乘法过程完毕。接下来从 c[0]开始向高位逐位处理进位问题。c[0]留下5，把4 加到c[1]上，c[1]变为51
后，应留下1，把5 加到c[2]上……最终使得c 里的每个元素都是1 位数，结果就算出来了：
规律：一个数的第i位和另一个数的第j位相乘所得的数，一定是要累加到结果的第i+j位上。这里i,j都是从右往 左，从0开始数。
大整数除法
double变量的精度也不足以表示一个100位的整数。一般我们称这种基本数据类型无法表示的整数为大整数。如何表示和存放大整数呢？基本的思想就是：用数组存放和表示大整数。一个数组元素，存放大整数中的一位。
那么，如何解决类似大整数这样的高精度计算问题呢？
大数是指计算的数值非常大或者对运算的精度要求非常高，用已知的数据类型无法表示的数值。设计思想如下：
2.开一个比较大的整型数组，数组的元素代表数组的某一位或者某几位。
3.通过对数组元素的运算模拟大数的运算。
4.将数组输出。
大整数加法
问题：求两个不超过200位的非负整数的和
思路：题目很明确告诉是很长的大整数相加，所以采用大数的加法；开一个整型数组，模拟加法：注意加法是尾对齐的。注意：1.不需要特殊的数据结构；2.大数一般使用数组模拟。
首先要解决的就是存储200 位整数的问题。显然，任何C/C++固有类型的变量都无法保存它。最直观的想法是可以用一个字符串来保存它。字符串本质上就是一个字符数组，因此为了编程更方便，我们也可以用数组unsigned an[200]来保存一个200 位的整数，让an[0]存放个位数，an[1]存放十位数，an[2]存放百位数……
那么如何实现两个大整数相加呢？方法很简单，就是模拟小学生列竖式做加法，从个位开始逐位相加，超过或达到10 则进位。也就是说，用unsigned an1[201]保存第一个数，用unsigned an2[200]表示第二个数，然后逐位相加，相加的结果直接存放在an1 中。要注意处理进位。另外，an1 数组长度定为201，是因为两个200 位整数相加，结果可能会有201 位。
实际编程时，不一定要费心思去把数组大小定得正好合适，稍微开大点也无所谓，以免不小心没有算准这个“正好合适”的数值，而导致数组小了，产生越界错误。
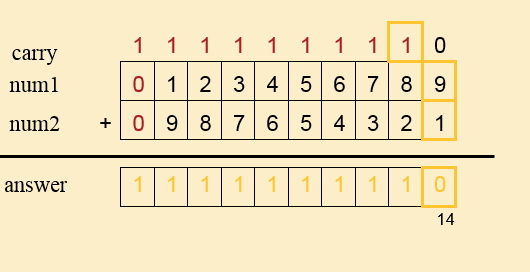
问 ： 123456789 + 987654321 ？
答： 把 123456789存在num1之中，987654321存在num2，結果存在answer中
#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
int an1[MAX_LEN+10];
int an2[MAX_LEN+10];
char szLine1[MAX_LEN+10];
char szLine2[MAX_LEN+10];
int main(void)
{
scanf("%s", szLine1);
scanf("%s", szLine2);
int i, j;
memset( an1, 0, sizeof(an1));
memset( an2, 0, sizeof(an2));
int nLen1 = strlen( szLine1);
for( j = 0, i = nLen1 - 1;i >= 0 ; i --)
an1[j++] = szLine1[i] - '0';
int nLen2 = strlen(szLine2);
for( j = 0, i = nLen2 - 1;i >= 0 ; i --)
an2[j++] = szLine2[i] - '0';
for( i = 0;i < MAX_LEN ; i ++ )
{ an1[i] += an2[i]; //逐位相加
if( an1[i] >= 10 )
{ //看是否要进位
an1[i] -= 10;
an1[i+1] ++; //进位
}
}
for( i = MAX_LEN; (i >= 0) && (an1[i] == 0); i -- ) ;
if(i>=0)
for( ; i >= 0; i--)
printf("%d", an1[i]);
else printf("0");
return 0;
}
大整数乘法
问题：求两个不超过200 位的非负整数的积。输入数据有两行，每行是一个不超过200 位的非负整数，没有多余的前导0。输出要求一行，即相乘后的结果。结果里不能有多余的前导0，即如果结果是342，那么就不能输出为0342。
比如说要计算 835×49:
先算835×9。5×9 得到45 个1，3×9 得到27 个10，8×9 得到72 个100。由于不急于处理进位，所以835×9算完后，结果如下：
接下来算4×5。此处4×5 的结果代表20 个10，因此要 c[1]+=20，变为：
再下来算4×3。此处4×3 的结果代表12 个100，因此要 c[2]+= 12，变为：
最后算 4×8。此处4×8 的结果代表 32 个1000，因此要 c[3]+= 32，变为：
规律：一个数的第i位和另一个数的第j位相乘所得的数，一定是要累加到结果的第i+j位上。这里i,j都是从右往 左，从0开始数。
#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
int main(void)
{
int i, j;
int len1,len2;
int a[MAX_LEN+10],b[MAX_LEN+10],c[MAX_LEN*2+10];
char str1[MAX_LEN+10],str2[MAX_LEN+10];
for(i=0;i<MAX_LEN+10;i++) a[i]=b[i]=0;
for(i=0;i<MAX_LEN*2+10;i++) c[i]=0;
gets(str1); //按字符串形式读入第一个整数
gets(str2);
len1=strlen(str1);
for(j=0,i=len1-1; i>=0; i--)//把数字倒过来
a[j++]=str1[i]-'0';
len2=strlen(str2);
for(j=0,i=len2-1; i>=0; i--)//倒转第二个整数
b[j++]=str2[i]-'0';
for(i=0; i<len2; i++)//用第二个数乘以第一个数,每次一位
{
for(j=0; j<len1; j++)
c[i+j]+= b[i]*a[j]; //先乘起来,后面统一进位
}
for(i=0; i<MAX_LEN*2; i++)//循环统一处理进位问题
{
if(c[i]>=10)
{
c[i+1]+=c[i]/10;
c[i]%=10;
}
}
for(i=MAX_LEN*2; (c[i]==0)&&(i>=0); i--);//跳过高位的0
if(i>=0)
for(;i>=0;i--)
printf("%d", c[i]);
else
printf("0");
return 0;
}
大整数除法
基本的思想是反复做减法，看看从被除数里最多能减去多少个除数，商就是多少。一个一个减显然太慢，如何减得更快一些呢？以7546除以23 为例来看一下：开始商为0。先减去23 的100 倍，就是2300，发现够减3次，余下646。于是商的值就增加300。然后用646 减去230，发现够减2次，余下186，于是商的值增加20。最后用186 减去 23，够减8 次，因此最终商就是328。
所以本题的核心是要写一个大整数的减法函数，然后反复调用该函数进行减法操作。 计算除数的10倍、100倍的时候，不用做乘法，直接在除数后面补0 即可。
#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
char szLine1[MAX_LEN + 10];
char szLine2[MAX_LEN + 10];
int an1[MAX_LEN + 10]; //被除数, an1[0]对应于个位
int an2[MAX_LEN + 10]; //除数, an2[0]对应于个位
int aResult[MAX_LEN + 10]; //存放商，aResult[0]对应于个位
//长度为 nLen1 的大整数p1 减去长度为nLen2 的大整数p2
//结果放在p1 里，返回值代表结果的长度
//如不够减返回-1，正好减完返回 0
int Substract( int * p1, int * p2, int nLen1, int nLen2)
{
int i;
if( nLen1 < nLen2 )
return -1;
//下面判断p1 是否比p2 大，如果不是，返回-1
if( nLen1 == nLen2 )
{
for( i = nLen1-1; i >= 0; i -- )
{
if( p1[i] > p2[i] ) break; //p1>p2
else if( p1[i] < p2[i] ) return -1; //p1<p2
}
}
for( i = 0; i < nLen1; i ++ )
{ //要求调用本函数确保当i>=nLen2 时，p2[i] ＝ 0
p1[i] -= p2[i];
if( p1[i] < 0 )
{
p1[i]+=10;
p1[i+1] --;
}
}
for( i = nLen1 -1 ; i >= 0 ; i-- )
if( p1[i] )//找到最高位第一个不为0
return i + 1;
return 0;//全部为0，说明两者相等
}
int main()
{
int t, n;
scanf("%d", &n);
for( t = 0; t < n; t ++ )
{
scanf("%s", szLine1);
scanf("%s", szLine2);
int i, j;
int nLen1 = strlen( szLine1);
memset( an1, 0, sizeof(an1));
memset( an2, 0, sizeof(an2));
memset( aResult, 0, sizeof(aResult));
for( j = 0, i = nLen1 - 1;i >= 0 ; i --)
an1[j++] = szLine1[i] - '0';
int nLen2 = strlen(szLine2);
for( j = 0, i = nLen2 - 1;i >= 0 ; i --)
an2[j++] = szLine2[i] - '0';
if( nLen1 < nLen2 )
{
printf("0\n");
continue;
}
int nTimes = nLen1 - nLen2;
if(nTimes > 0)
{
for( i = nLen1 -1; i >= nTimes; i -- )
an2[i] = an2[i-nTimes];//朝高位移动
for( ; i >= 0; i--)//低位补0
an2[i] = 0;
nLen2 = nLen1;
}
for( j = 0 ; j <= nTimes; j ++ )
{
int nTmp;
//一直减到不够减为止
//先减去若干个 an2×(10 的 nTimes 次方)，
//不够减了，再减去若干个 an2×(10 的 nTimes-1 次方)，......
while( (nTmp = Substract(an1, an2+j, nLen1, nLen2-j)) >= 0)
{
nLen1 = nTmp;
aResult[nTimes-j]++; //每成功减一次，则将商的相应位加1
}
}
//下面输出结果，先跳过高位0
for( i = MAX_LEN ; (i >= 0) && (aResult[i] == 0); i -- );
if( i >= 0)
for( ; i>=0; i--)
printf("%d", aResult[i]);
else
printf("0");
printf("\n");
}
return 0;
}
按照上面的思路，我们可以把它统一起来做成一个大数包！我花了一个星期来完成这个大数包，不过测试数据很少，不太敢保证绝对正确，发出来仅供参考！
这个大数包产生大素数比较慢，如果需要产生大素数的比较快的大数包请参考这里！
http://blog.csdn.net/lishuhuakai/article/details/9083339
//下面的代码勉强算是bignum_beta1版本！
//实现了大整数的加减乘除四则运算,以及求两个整数的最大公约数,以及求乘法逆,miller_rabin素性检验,平方_乘法算法
//不足之处，位数还很难扩展至几千位,以及运算速度有一点慢,既然是beta1,说明bug还是挺多的
//程序缺少测试数据来测试,所以有的结果不敢保证其正确性
//由于使用c++复写了很多运算符,加入这个文件之后,大数bignum可以看做是一个如同如同int一样的基本类型
//可以像int一样加减乘除和输入输出
#include<iostream>
#include<string>
#include<ctime>//用于产生随机数
using namespace std;
const int base=1000;//base用来表示数组中每个数的进制,逢base向前一位进1
const int MAX_LEN=300;//数组的最大长度
class bigNum{
public:
int num[MAX_LEN];
int len;
int flag;//增设一个标志，表示正负，这样大数包就可以扩展置负数
friend istream& operator>>(istream& input,bigNum &obj);
friend ostream& operator<<(ostream& output,bigNum& obj);
bigNum &operator=(const bigNum &s);//对于"="号的重载
//类的赋值运算符"="只能重载为成员函数，而不能把它重载为友元函数
bigNum();//构造函数
void eucli_setnum(int x);//设置数值
};
void bigNum::eucli_setnum(int x)//设置这个函数主要应对扩展的欧几里德算法
{
num[0]=x;
if(x!=0)
len=1;
else len=0;
}
bigNum::bigNum()//构造函数
{
memset(num,0,sizeof(num));//清零
len=0;
flag=1;//默认的数为正数
}
//关于下面的运算符重载函数，有一点需要特别记住，那就是len一定要记得更新，不然会出错！
//以下的几个函数都是逻辑运算符的重载函数
bool operator==(bigNum &a,bigNum &b)//"=="号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)
if(a.num[i]!=b.num[i])
return false;
return true;
}
bool operator!=(bigNum &a,bigNum &b)//"!="号的重载
{
for(int i=0;i<MAX_LEN;i++)
if(a.num[i]!=b.num[i])
return true;//只要有一个不相等,就返回true
return false;
}
/*
bool operator!=(bigNum &a,int &b)//"!="号的重载
{
if(a.num[0]!=b)
return false;//只要有一个不相等,就返回true
for(int i=1;i<MAX_LEN-1;i++)
if(a.num[i]!=0)
return false;
return true;
}*/
bool operator>(bigNum &a,bigNum &b)//">"号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]>b.num[i])
return true;
else return false;
return false;//两个数相同也返回false
}
bool operator<(bigNum &a,bigNum &b)//"<"号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
{
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]<b.num[i])
return true;
else
return false;
}
return false;
}
bool operator<=(bigNum &a,bigNum &b)
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]<b.num[i])
return true;
else
return false;
return true;//最后相等返回true
}
bool operator>=(bigNum &a,bigNum &b)
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]>b.num[i])
return true;
else
return false;
return true;//最后相等返回true
}
bigNum &bigNum::operator=(const bigNum &s)//"="号的重载
{
if(this==&s) return *this;//防止s=s
for(int i=0;i<MAX_LEN;i++)
num[i]=s.num[i];
len=s.len;
flag=s.flag;
}
//以下几个函数是四则运算符的重载函数
bigNum operator-(bigNum a,bigNum b);//声明,防止编译出错
bigNum operator+(bigNum a,bigNum b)//加法的重载
{
bigNum sum;//存储结果
int i;
if(a.flag<0 && b.flag>0)//a为负,b为正,则a+b=b-|a|
{
a.flag=1;//这里对a进行了修改(将a变为正数),以便于进行减法运算,这也是重写不用引用的reason
sum=b-a;
if(b>a)
sum.flag=1;//结果为正
else
sum.flag=-1;//结果为负
return sum;
}
if(a.flag>0 && b.flag<0)//a为正,b为负,则b+a=a-|b|
{
b.flag=1;
sum=a-b;
if(a>b)
sum.flag=1;//结果为正
else
sum.flag=-1;//结果为负
return sum;
}
//余下的情况是a,b两者符号相同,即a+b=(|a|+|b|)*flag,flag与a,b符号一致
for(i=0;i<MAX_LEN;i++)
{
sum.num[i]+=a.num[i]+b.num[i];
if(sum.num[i]>base)//超出base,则要进位
{
sum.num[i]-=base;
sum.num[i+1]++;
}
if(sum.num[i]!=0) sum.len=i+1;//len要同步更新
}
sum.flag=a.flag;//如果a,b不是一正一负,那么a,b必定同号
return sum;
}
bigNum operator-(bigNum a,bigNum b)//减法的重载
{
bigNum sum;//存储结果
if(a.flag<0 && b.flag>0)//a为负,b为正,则a-b=-(|a|+|b|)
{
a.flag=1;
sum=b+a;
sum.flag=-1;//两个负数相加，结果一定为负数
return sum;
}
if(a.flag>0 && b.flag<0 && a>b)//a为正,b为负,则a-b=|a|+|b|
{
b.flag=1;
sum=b+a;
sum.flag=1;//两个正数相加，结果一定为正数
return sum;
}
//下面a,b的符号值一致
if(a<b)//a<b,则|a|-|b|<0,转化为-(|b|-|a|)
{
sum=b-a;
sum.flag=-b.flag;
return sum;
}
//下面表示的就是|a|>|b|,且a,b同号
for(int i=0;i<MAX_LEN;i++)
{
a.num[i]-=b.num[i];
if(a.num[i]<0)//不够减时向前借位
{
a.num[i]+=base;
a.num[i+1]--;
}
if(a.num[i]!=0) a.len=i+1;//len要同步更新
}
return a;
}
bigNum operator*(bigNum &a,bigNum &b)//对于乘法的重载
{//乘法的flag已经设置完毕
bigNum sum;
int i,j;
for(i=0;i<b.len;i++)//用第二个数b乘以第一个数a
{
for(j=0;j<a.len;j++)
sum.num[i+j]+=b.num[i]*a.num[j];//先乘起来,后面统一进位
}
for(i=0;i<MAX_LEN;i++)//循环统一处理进位问题
{
if(sum.num[i]>=base)
{
sum.num[i+1]+=sum.num[i]/base;
sum.num[i]%=base;
}
if(sum.num[i]!=0) sum.len=i+1;//len要同步更新
}
//现在设置数的正负
if(a.flag+b.flag==0) sum.flag=-1;
else sum.flag=a.flag;
return sum;
}
int substract(int *p1,int *p2,int n1,int n2)
{
int i;
//被除数不能小于除数
if(n1<n2) return -1;//p2数的长度不能大于p1数的长度
if(n1==n2)//两数长度一致情况下(所占用数组长度),p2数要小于p1数
{
for(i=n1-1;i>=0;i--)
{
if(p1[i]>p2[i]) break;
else if(p1[i]<p2[i]) return -1;
}
}
for(i=0;i<n1;i++)
{//减去一个p2值
p1[i]-=p2[i];
if(p1[i]<0)
{
p1[i]+=base;
p1[i+1]--;
}
}
for(i=n1-1;i>=0;i--)
if(p1[i])
return i+1;//返回所占用的数组长度
return 0;
}
bigNum operator/(bigNum a,bigNum b)//除法的重载
{//除法的flag设置完毕
bigNum sum;
int i,j;
if(a<b)//a<b时返回0
return sum;
int nTimes=a.len-b.len;
if(nTimes>0)
{
for(i=a.len-1;i>=nTimes;i--)
b.num[i]=b.num[i-nTimes];//朝高位移动
for(;i>=0;i--)
b.num[i]=0;//低位补0
b.len=a.len;
}
for(j=0;j<=nTimes;j++)
{
int nTmp;
//一直减到不够减为止
while((nTmp=substract(a.num,b.num+j,a.len,b.len-j))>=0)
{
a.len=nTmp;
sum.num[nTimes-j]++;//每减成功一次,则将商的对应为加1
}
if(sum.len==0 && sum.num[nTimes-j]!=0)
sum.len=nTimes-j+1;//同步更新len
}
//现在设置数的正负
if(a.flag+b.flag==0) sum.flag=-1;
else sum.flag=a.flag;
return sum;
}
bigNum operator%(bigNum &a,bigNum &b)//取模运算的重载
{
return a-b*(a/b);
}
istream& operator>>(istream& input,bigNum& obj)//重载输入函数
{//输入flag已经设置完毕
string str;
input>>str;
int l=str.size();//l为字符串长度
int i,k,j;
for(j=0,i=base;i!=1;)
if(i>0)
{
j++;
i=i/10;
}//j用来表示base的位数
int p=l/j,q=l%j;//输入的数按照每个可以存放j个的标准,恰好放进,一共占用p个位置
if(q) obj.len=p+1;//当然,不一定恰好放进,就需要p+1个位置来放
else obj.len=p;
if(str[0]=='-')//输入为负数
obj.flag=-1;
else
obj.flag=1;//设置符号位,正数则flag为1，否则为-1
for(i=0;i<q;i++)//用来存放不能整除的高位部分
{
if(str[i]=='-') i++;//如果是负数的话,第一位不用处理
obj.num[p]=obj.num[p]*10+str[i]-'0';
}
p--;
for(;p>=0;p--)//下面的字符，以j为一组,字符个数恰好能够被j整除,一组组存入num数组里
{
for(k=1;k<=j;k++)
{
obj.num[p]=obj.num[p]*10+str[i]-'0';
i++;
}
}
return input;
}
ostream& operator<<(ostream& output,bigNum& obj)
{//输出flag就已经设置好了
int i;
for(i=MAX_LEN-1; (i>=0)&&(obj.num[i]==0);i--);
if(i>=0)
{
if(obj.flag==-1) output<<'-';
for(;i>=0;i--)
output<<obj.num[i];
}
else
output<<'0';//整个数组都是0
return output;
}
bigNum extended_euclidean(bigNum n,bigNum m,bigNum &x,bigNum &y)//扩展的欧几里德算法的另一种形式
{
bigNum x1, x2, x3=n;
x1.eucli_setnum(1);
x2.eucli_setnum(0);
bigNum y1, y2, y3=m;
y1.eucli_setnum(0);
y2.eucli_setnum(1);
bigNum zero;
while(x3%y3!=zero)
{
bigNum d=x3/y3;
bigNum t1,t2,t3;
t1=x1-d*y1;
t2=x2-d*y2;
t3=x3-d*y3;
x1=y1; x2=y2; x3=y3;
y1=t1; y2=t2; y3=t3;
}
x=y1; y=y2;
return y3;
}
bigNum gcd(bigNum &n,bigNum &m)//求两个大数的最大公约数
{
bigNum x,y;
return extended_euclidean(n,m,x,y);
}
//求乘法逆其实也没有特别好的算法，主要还是依靠欧几里德算法
bigNum mutirinverse(bigNum &n,bigNum &m)//求乘法逆
{
bigNum x,y;
extended_euclidean(m,n%m,x,y);
return x;
}
//平方——乘法算法
bigNum Square_and_Mutiply(bigNum a,bigNum m,bigNum n)
{
bigNum sum,zero,two;
two.eucli_setnum(2);
sum.eucli_setnum(1);
int length=1;
int bin[300];
//先将m转化为二进制
do
{
sum=m%two;
bin[length++]=sum.num[0];
m=m/two;
}while(m!=zero);
sum.eucli_setnum(1);
while(length>=0)
{
sum=(sum*sum)%n;
if(bin[length]==1)
{
sum=(sum*a)%n;
}
length--;
}
return sum;
}
//最后一个函数,用于素数判定的Miller-Rabin算法
bool wintess(bigNum a,bigNum n)
{
bigNum m,x,y,one,two,zero;
one.eucli_setnum(1);two.eucli_setnum(2);
bigNum i,j;
m=n-one;
while(m%two==zero)
{
m=m/two;
j=j+one;
}
x=Square_and_Mutiply(a,m,n);
for(i.eucli_setnum(1);i<=j;i=i+one)
{
y=Square_and_Mutiply(x,two,n);
if((y==one)&&(x!=one)&&(x!=n-one))
return true;
x=y;
}
if(y!=one) return true;
return false;
}
bool Miller_Robin(int times,bigNum &n)
//n为大于3的奇数,输出n是否通过素性检验
{
bigNum a,one,two,random;
one.eucli_setnum(1);two.eucli_setnum(2);
if(n==one) return false; if(n==two) return true;
srand((unsigned)time(0));
for(int i=1;i<=times;i++)
{
random.eucli_setnum(rand());
a=random%(n-two)+two;
if(wintess(a,n)) return false;
}
return false;
}
int main()
{
bigNum a,b;
while(1)
{
cin>>a;
cin>>b;
cout<<a*b<<endl;
}
system("pause");
return 0;
}
发个最终的beta_2版本吧！再也不改了！
//下面的代码勉强算是bignum_beta2版本！
//实现了大整数的加减乘除四则运算,以及求两个整数的最大公约数,以及求乘法逆,miller_rabin素性检验,平方_乘法算法
//不足之处,位数还很难扩展至几千位,以及运算速度有一点慢,既然是beta1,说明bug还是挺多的
//程序缺少测试数据来测试,所以有的结果不敢保证其正确性
//由于使用c++复写了很多运算符,加入这个文件之后,大数bignum可以看做是一个如同如同int一样的基本类型
//可以像int一样加减乘除和输入输出
#include<iostream>
#include<string>
#include<ctime>//用于产生随机数
using namespace std;
const int base=1000;//base用来表示数组中每个数的进制,逢base向前一位进1
const int MAX_LEN=300;//数组的最大长度
class bigNum{
public:
int num[MAX_LEN];
int len;
int flag;//增设一个标志,表示正负,这样大数包就可以扩展置负数
friend istream& operator>>(istream& input,bigNum &obj);
friend ostream& operator<<(ostream& output,bigNum& obj);
bigNum &operator=(const bigNum &s);//对于"="号的重载
bigNum &bigNum::operator=(const int &num);
//类的赋值运算符"="只能重载为成员函数,而不能把它重载为友元函数
bigNum();//构造函数
};
bigNum::bigNum()//构造函数
{
memset(num,0,sizeof(num));//清零
len=0;
flag=1;//默认的数为正数
}
//关于下面的运算符重载函数,有一点需要特别记住,那就是len一定要记得更新,不然会出错！
//以下的几个函数都是逻辑运算符的重载函数
/********************************************************
关于等于的判断
********************************************************/
bool operator==(bigNum &a,bigNum &b)//两个大整数之间"=="号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)
if(a.num[i]!=b.num[i])
return false;
return true;
}
bool operator==(bigNum &a,int b)//大整数与整数之间"=="号的重载
{
if(a.num[0]==b)
{
for(int i=1;i<MAX_LEN;i++)
if(a.num[i]!=0)
return false;
return true;
}
return false;
}
/**************************************************************
关于不等号的重载
***************************************************************/
bool operator!=(bigNum &a,bigNum &b)//两个大整数之间"!="号的重载
{
for(int i=0;i<MAX_LEN;i++)
if(a.num[i]!=b.num[i])
return true;//只要有一个不相等,就返回true
return false;
}
bool operator!=(bigNum &a,int b)//大整数与整数之间"!="号的重载
{
if(a.num[0]!=b)
return true;
return false;
}
/**************************************************************
关于大于号的重载
***************************************************************/
bool operator>(bigNum &a,bigNum &b)//">"号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]>b.num[i])
return true;
else return false;
return false;//两个数相同也返回false
}
/***************************************************************
关于小于号的重载
****************************************************************/
bool operator<(bigNum &a,bigNum &b)//两个大整数之间"<"号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
{
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]<b.num[i])
return true;
else
return false;
}
return false;
}
/***************************************************************
关于小于等于号的重载
****************************************************************/
bool operator<=(bigNum &a,bigNum &b)
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]<b.num[i])
return true;
else
return false;
return true;//最后相等返回true
}
/****************************************************************
关于大于等于号的重载
*****************************************************************/
bool operator>=(bigNum &a,bigNum &b)
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相等,必定有一大一小
if(a.num[i]>b.num[i])
return true;
else
return false;
return true;//最后相等返回true
}
/****************************************************************
对于等于的重载
*****************************************************************/
bigNum &bigNum::operator=(const bigNum &s)//两个大整数之间"="号的重载
{
if(this==&s) return *this;//防止s=s
for(int i=0;i<MAX_LEN;i++)
num[i]=s.num[i];
len=s.len;
flag=s.flag;
return *this;
}
bigNum &bigNum::operator=(const int &a)//大整数和整数之间"="的重载
{
int i;
memset(num,0,sizeof(num));//先清零
len=1;
num[0]=a;
for(i=0;i<MAX_LEN;i++)//主要防止a>base
{
if(num[i]>base)
{
len++;//len要时时更新
num[i+1]+=num[i]/base;
num[i]%=base;
}
else break;
}
return *this;
}
//以下几个函数是四则运算符的重载函数
bigNum operator-(bigNum a,bigNum b);//声明,防止编译出错
/***********************************************************
对于加法的重载
***********************************************************/
bigNum operator+(bigNum a,bigNum b)//加法的重载
{
bigNum sum;//存储结果
int i;
if(a.flag<0 && b.flag>0)//a为负,b为正,则a+b=b-|a|
{
a.flag=1;//这里对a进行了修改(将a变为正数),以便于进行减法运算,这也是重写不用引用的reason
sum=b-a;
//符号位要特别处理，因为在处理加减号的时候并没有特别强调符号
if(b>a)
sum.flag=1;//结果为正
else
sum.flag=-1;//结果为负
return sum;
}
if(a.flag>0 && b.flag<0)//a为正,b为负,则b+a=a-|b|
{
b.flag=1;
sum=a-b;
if(a>b)
sum.flag=1;//结果为正
else
sum.flag=-1;//结果为负
return sum;
}
//余下的情况是a,b两者符号相同,即a+b=(|a|+|b|)*flag,flag与a,b符号一致
for(i=0;i<MAX_LEN;i++)
{
sum.num[i]+=a.num[i]+b.num[i];
if(sum.num[i]>base)//超出base,则要进位
{
sum.num[i]-=base;
sum.num[i+1]++;
}
if(sum.num[i]!=0) sum.len=i+1;//len要同步更新
}
sum.flag=a.flag;//如果a,b不是一正一负,那么a,b必定同号
return sum;
}
bigNum operator+(bigNum a,int b)//大整数和整数之间的加法
{
int sum,carry,i;
sum=a.num[0]+b;
for(i=0,carry=0;i<MAX_LEN;i++)
{
if(sum>base)
{
carry=sum/base;//向前的进位
a.num[i]=sum%base;
a.num[i+1]+=carry;
}
if(carry==0)
break;
}
if(i>a.len) a.len=i;
return a;
}
bigNum operator+(int b,bigNum a)
{
int sum,carry,i;
sum=a.num[0]+b;
for(i=0,carry=0;i<MAX_LEN;i++)
{
if(sum>base)
{
carry=sum/base;//向前的进位
a.num[i]=sum%base;
a.num[i+1]+=carry;
}
if(carry==0)
break;
}
if(i>a.len) a.len=i;
return a;
}
/*************************************************************
对于减法的重载
************************************************************/
bigNum operator-(bigNum a,bigNum b)//减法的重载
{
bigNum sum;//存储结果
if(a.flag<0 && b.flag>0)//a为负,b为正,则a-b=-(|a|+|b|)
{
a.flag=1;
sum=b+a;
sum.flag=-1;//两个负数相加,结果一定为负数
return sum;
}
if(a.flag>0 && b.flag<0 && a>b)//a为正,b为负,则a-b=|a|+|b|
{
b.flag=1;
sum=b+a;
sum.flag=1;//两个正数相加,结果一定为正数
return sum;
}
//下面a,b的符号值一致
if(a<b)//a<b,则|a|-|b|<0,转化为-(|b|-|a|)
{
sum=b-a;
sum.flag=-b.flag;
return sum;
}
//下面表示的就是|a|>|b|,且a,b同号
for(int i=0;i<MAX_LEN;i++)
{
a.num[i]-=b.num[i];
if(a.num[i]<0)//不够减时向前借位
{
a.num[i]+=base;
a.num[i+1]--;
}
if(a.num[i]!=0) a.len=i+1;//len要同步更新
}
return a;
}
/****************************************************
关于乘法的重载
*****************************************************/
bigNum operator*(bigNum &a,bigNum &b)//对于乘法的重载
{//乘法的flag已经设置完毕
bigNum sum;
int i,j;
for(i=0;i<b.len;i++)//用第二个数b乘以第一个数a
{
for(j=0;j<a.len;j++)
sum.num[i+j]+=b.num[i]*a.num[j];//先乘起来,后面统一进位
}
for(i=0;i<MAX_LEN;i++)//循环统一处理进位问题
{
if(sum.num[i]>=base)
{
sum.num[i+1]+=sum.num[i]/base;
sum.num[i]%=base;
}
if(sum.num[i]!=0) sum.len=i+1;//len要同步更新
}
//现在设置数的正负
if(a.flag+b.flag==0) sum.flag=-1;//两数符号不同
else sum.flag=a.flag;//符号相同
return sum;
}
/**************************************************************
关于除法的重载
**************************************************************/
int substract(int *p1,int *p2,int n1,int n2)//核心减法函数
{
int i;
//除数不能大于被除数
if(n1<n2) return -1;//p2数的长度不能大于p1数的长度
if(n1==n2)//两数长度一致情况下(所占用数组长度),p2数要小于p1数
{
for(i=n1-1;i>=0;i--)
{
if(p1[i]>p2[i]) break;
else if(p1[i]<p2[i]) return -1;
}
}
for(i=0;i<n1;i++)
{//减去一个p2值
p1[i]-=p2[i];
if(p1[i]<0)//向前借位
{
p1[i]+=base;
p1[i+1]--;
}
}
for(i=n1-1;i>=0;i--)
if(p1[i])
return i+1;//返回所占用的数组长度
return 0;
}
bigNum operator/(bigNum a,bigNum b)//两个大整数之间除法的重载
{//除法的flag设置完毕
bigNum sum;
int i,j;
if(a<b)//a<b时返回0
return sum;
int nTimes=a.len-b.len;
if(nTimes>0)
{
for(i=a.len-1;i>=nTimes;i--)
b.num[i]=b.num[i-nTimes];//除数朝高位移动
for(;i>=0;i--)
b.num[i]=0;//低位补0
b.len=a.len;
}
for(j=0;j<=nTimes;j++)
{
int nTmp;
//一直减到不够减为止
while((nTmp=substract(a.num,b.num+j,a.len,b.len-j))>=0)
{
a.len=nTmp;
sum.num[nTimes-j]++;//每减成功一次,则将商的对应值为加1
}
if(sum.len==0 && sum.num[nTimes-j]!=0)
sum.len=nTimes-j+1;//同步更新len
}
//现在设置数的正负
if(a.flag+b.flag==0) sum.flag=-1;
else sum.flag=a.flag;
return sum;
}
/******************************************************
关于取模符号的重载
*******************************************************/
bigNum operator%(bigNum &a,bigNum &b)//取模运算的重载
{
return a-b*(a/b);
}
/*******************************************************
关于输入函数的重载
********************************************************/
istream& operator>>(istream& input,bigNum& obj)//重载输入函数
{//输入flag已经设置完毕
string str;
input>>str;
int l=str.size();//l为字符串长度
int i,k,j;
for(j=0,i=base;i!=1;)
if(i>0)
{
j++;
i=i/10;
}//j用来表示base的位数
int p=l/j,q=l%j;//输入的数按照每个可以存放j个的标准,恰好放进,一共占用p个位置
if(q) obj.len=p+1;//当然,不一定恰好放进,就需要p+1个位置来放
else obj.len=p;
if(str[0]=='-')//输入为负数
obj.flag=-1;
else
obj.flag=1;//设置符号位,正数则flag为1,否则为-1
for(i=0;i<q;i++)//用来存放不能整除的高位部分
{
if(str[i]=='-') i++;//如果是负数的话,第一位不用处理
obj.num[p]=obj.num[p]*10+str[i]-'0';
}
p--;
for(;p>=0;p--)//下面的字符,以j为一组,字符个数恰好能够被j整除,一组组存入num数组里
{
for(k=1;k<=j;k++)
{
obj.num[p]=obj.num[p]*10+str[i]-'0';
i++;
}
}
return input;
}
/*******************************************************
关于输出函数的重载
********************************************************/
ostream& operator<<(ostream& output,bigNum& obj)
{//输出flag就已经设置好了
int i;
for(i=MAX_LEN-1; (i>=0)&&(obj.num[i]==0);i--);
if(i>=0)
{
if(obj.flag==-1) output<<'-';
for(;i>=0;i--)
output<<obj.num[i];
}
else
output<<'0';//整个数组都是0
return output;
}
/***********************************************************
扩展的欧几里德算法
***********************************************************/
bigNum extended_euclidean(bigNum n,bigNum m,bigNum &x,bigNum &y)//扩展的欧几里德算法的另一种形式
{
bigNum x1, x2, x3=n;
x1=1;
x2=0;
bigNum y1, y2, y3=m;
y1=0;
y2=1;
bigNum zero;
while(x3%y3!=0)
{
bigNum d=x3/y3;
bigNum t1,t2,t3;
t1=x1-d*y1;
t2=x2-d*y2;
t3=x3-d*y3;
x1=y1; x2=y2; x3=y3;
y1=t1; y2=t2; y3=t3;
}
x=y1; y=y2;
return y3;
}
/********************************************************
求两个大数的最大公约数
*********************************************************/
bigNum gcd(bigNum &n,bigNum &m)//求两个大数的最大公约数
{
bigNum x,y;
return extended_euclidean(n,m,x,y);
}
/*****************************************************
求乘法逆其实也没有特别好的算法,主要还是依靠欧几里德算法
*****************************************************/
bigNum mutirinverse(bigNum &n,bigNum &m)//求乘法逆
{
bigNum x,y;
extended_euclidean(m,n%m,x,y);
return x;
}
/****************************************************
平方——乘法算法
*****************************************************/
bigNum Square_and_Mutiply(bigNum a,bigNum m,bigNum n)
{
bigNum sum,zero,two;
two=2;//由于大整数与整数之间的乘法没有实现，所以就用大整数代替了！
sum=1;
int length=0;
int bin[5000];
//先将m转化为二进制
do
{
sum=m%two;
bin[length++]=sum.num[0];
m=m/two;
}while(m!=0);//不得不说，效率的确很低
sum=1;
while(length>=0)
{
sum=(sum*sum)%n;
if(bin[length]==1)
{
sum=(sum*a)%n;
}
length--;
}
return sum;
}
/****************************************************
最后一个函数,用于素数判定的Miller-Rabin算法
*****************************************************/
bool wintess(bigNum a,bigNum n)
{
bigNum m,x,y,one,two,zero;
one=1;two=2;
bigNum i,j;
m=n-one;
while(m%two==0)
{
m=m/two;
j=j+1;
}
x=Square_and_Mutiply(a,m,n);
for(i=1;i<=j;i=i+one)
{
y=Square_and_Mutiply(x,two,n);
if((y==1)&&(x!=1)&&(x!=n-one))
return true;//返回true时,n为和数
x=y;
}
if(y!=1) return true;
return false;
}
bool Miller_Robin(int times,bigNum &n)
//n为大于3的奇数,输出n是否通过素性检验
{
bigNum a,one,two,random;
one=1;two=2;
if(n==1) return false; if(n==2) return true;
srand((unsigned)time(0));
for(int i=1;i<=times;i++)
{
random=rand();
a=random%(n-two)+two;
if(wintess(a,n)) return false;
}
return true;
}
/***************************************************
用于伪素数的生成
***************************************************/
const static int PrimeTable[550]=
{ 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,
37, 41, 43, 47, 53, 59, 61, 67, 71, 73,
79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
131, 137, 139, 149, 151, 157, 163, 167, 173, 179,
181, 191, 193, 197, 199, 211, 223, 227, 229, 233,
239, 241, 251, 257, 263, 269, 271, 277, 281, 283,
293, 307, 311, 313, 317, 331, 337, 347, 349, 353,
359, 367, 373, 379, 383, 389, 397, 401, 409, 419,
421, 431, 433, 439, 443, 449, 457, 461, 463, 467,
479, 487, 491, 499, 503, 509, 521, 523, 541, 547,
557, 563, 569, 571, 577, 587, 593, 599, 601, 607,
613, 617, 619, 631, 641, 643, 647, 653, 659, 661,
673, 677, 683, 691, 701, 709, 719, 727, 733, 739,
743, 751, 757, 761, 769, 773, 787, 797, 809, 811,
821, 823, 827, 829, 839, 853, 857, 859, 863, 877,
881, 883, 887, 907, 911, 919, 929, 937, 941, 947,
953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019,
1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087,
1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153,
1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229,
1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297,
1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381,
1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453,
1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523,
1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597,
1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663,
1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741,
1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823,
1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901,
1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993,
1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063,
2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131,
2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221,
2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293,
2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371,
2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437,
2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539,
2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621,
2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689,
2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749,
2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833,
2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909,
2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001,
3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083,
3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187,
3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259,
3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343,
3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433,
3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517,
3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581,
3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659,
3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733,
3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823,
3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911,
3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001
};//构建一个素数表,用于筛选大整数
/*********************************************************
素数的生成
**********************************************************/
bigNum Getprime()
{
bigNum sum,temp;
bigNum zero,two;
two=2;
int i,j,k=MAX_LEN/2;
bool flag=false;//flag=true表示数为合数，flag=false表示数可能为素数
srand((unsigned)time(0));
for(i=0;i<k;i++)//前期的实验数就小一点吧
sum.num[i]=rand()%base;//随机产生了一个大整数
if(sum.num[0]%2==0) sum.num[0]++;//保证为奇数
cout<<"运行之中… … … …"<<endl;
cout<<"随机产生的大整数为："<<endl;
cout<<sum<<endl;
cout<<endl;
while(!flag)
{
cout<<"正在进行素性检验… … … …"<<endl;
cout<<"参与检验的素数为："<<endl;
for(j=0;j<10;j++)
{
temp=PrimeTable[j];
cout<<temp<<endl;
if(sum%temp==0)
{
cout<<sum%temp<<endl;
flag=true;//表明sum是合数
break;
}
}
if(!flag)//通过了之前的素性检验
{
cout<<"第一轮素性检验通过… … … …"<<endl;
cout<<"正在进行Miller_Robin素性检验… … … …"<<endl;
if(Miller_Robin(1,sum))//进行1次Miller_Robin检验
return sum;//通过了就返回sum
else flag=true;//表明sum是和数,没有通过检验
}
if(flag)//如果没有通过检验,就+2,继续检验
sum=sum+2;
cout<<"运行之中… … … …"<<endl;
}
return sum;
}
int main()
{
bigNum a,b;
//cin>>a;
//cin>>b;
cout<<Getprime()<<endl;
system("pause");
return 0;
}
/***********************************************************
基本上就是这样了！这个程序我也不改了，做一个总结吧！这个程序
运行加减乘除还行，可是如果要用它生成大素数的话，速度远远不够，
本来我选择的数据结构就不太快，最快的应该是用2^n进制，而不是用
10^n进制，完全仿照计算机内部运算，用移位什么的操作，速度会快
上一大截，具体的做法可以参考这本书！
《密码编码学——加密方法的C与C十十实现(第二版)》
***********************************************************/