acm题目及我的程序（2）——Knight Moves (骑士跳跃) ——任意两点间的最短路径所有信息（算法2）

要求：

求出任意两点间的最短路径、最短路径个数及所有最短路径上的点

解决方法：

在搜索的过程中就开始求最短路径的长度，用变量代替回溯的值，若当前搜索的点已经超过当前最短路径长度，则从这个点回溯，从点出发的8个方向均不需要搜索，即在搜索树中，该点的儿子节点直接跳过；  该算法效率较高。

程序提供三种输入方法：求所有任意两点间的最短路径、个数及其点；求出这些数据并写入文件，输入两点坐标。

源代码如下：

/**/ /************************************************************************
 *  骑士遍历任意两点,求其长度小于等于6的路径个数,最短路径及其个数
 ************************************************************************/

#include  < STDIO.H >
#include  < STDLIB.H >
#include  < CONIO.H >
#include  < string .h >

#define  MAXLENGTH 8             // 棋盘边长
#define  MAXSTEP 10             // 最大步数
#define  MAXPATH 1000         // 所有路径最多个数
#define  FILENAMELENGTH 100     // 文件名长度
#define  MAXMINSTEP 6         // 最短步长最大数

// 定义棋盘点(i,j),i 为行,j为列
typedef  struct  
... {
    int i;        //棋盘上点行下标
    int j;        //棋盘上点列下标
} ChessPoint;

// 定义路径数据结构
typedef  struct
... {
    ChessPoint curpath[MAXSTEP];    //该条路径的路径数组
    int curstep;                    //该条路径的步数
} ALLPATH;

int  chess[MAXLENGTH + 1 ][MAXLENGTH + 1 ] = ... {0} ;     // 棋盘,行列下标均从1开始
int  offseti[ 9 ] = ... {0,-2,-1,+1,+2,+2,+1,-1,-2} ;     // i下标增量数组
int  offsetj[ 9 ] = ... {0,+1,+2,+2,+1,-1,-2,-2,-1} ;     // j下标增量数组
int  pathcount = 0 ;             // 路径的个数
int  pathstep[MAXPATH] = ... {0} ;     // 每一条路径步数数组
int  maxpathcount = 0 ;             // 路径个数最大值
int  maxminstep = 0 ;             // 最短路径个数最大值

/**/ /************************************************************************
 * 方向数组,存放已经走过的每一步的走向
 *     该数组初始化为0,第0号单元不用,第i个单元存放第i步的走向
 *     当前活动单元索引号为step
 ************************************************************************/
int  direction[MAXSTEP] = ... {0} ;

/**/ /************************************************************************
 * 路径数组,存放已经走过的每一步走向到达的点
 *     该数组初始化为0,第0号单元存放源点(srci,srcj)
 *     第i个单元存放第i-1个单元的点沿direction[i]方向走一步后的新点
 *     当前活动单元索引号为step
 ************************************************************************/
ChessPoint path[MAXSTEP];

/**/ /************************************************************************
 * 任意两点间所有路径数组,存放两点间的每一条路径
 *     该两点间的路径总数存于pathcount变量中
 ************************************************************************/
ALLPATH allpath[MAXPATH];

/**/ /************************************************************************
 * 函数说明: 
 *     knight 在点(i,j) 沿着 k 方向走一步,到达新点 (newi,newj)
 * 参数说明:
 *     i    : 走一步前的行下标 (i>=1 and i<=8)
 *     j    : 走一步前的列下标 (j>=1 and j<=8)
 *     k    : 方向 (k>=1 and k<=8)
 *     newi : 走一步后的行下标 (newi>=1 and newi<=8)
 *     newj : 走一步后的列下标 (newj>=1 and newj<=8)
 ************************************************************************/
void  new_point_at_direction( int  i, int  j, int  k, int   & newi, int   & newj)
... {
    newi=i+offseti[k];
    newj=j+offsetj[k];
}

/**/ /************************************************************************
 * 函数说明: 
 *     判断 knight 到达的新点 (newi,newj) 是否在棋盘上
 * 参数说明:
 *     newi : 新点行下标 (newi>=1 and newi<=8)
 *     newj : 新点列下标 (newj>=1 and newj<=8)
 * 返回值说明:
 *     true : 新点在棋盘上
 *     false: 新点不在棋盘上
 ************************************************************************/
bool  new_point_is_on_chessboard( int  newi, int  newj)
... {
    if((newi>=1 && newi<=MAXLENGTH) && (newj>=1 && newj<=MAXLENGTH))
        return true;
    return false;
}

// 求解前初始化各种参数初始化
void  initialize()
... {
    pathcount=0;

    for(int i=0;i<MAXLENGTH+1;i++)
        for(int j=0;j<MAXLENGTH+1;j++)
            chess[i][j]=0;

    for(int k=0;k<MAXPATH;k++)
        pathstep[k]=0;

    for(k=0;k<MAXSTEP;k++)
        path[k].i=path[k].j=0;
}

/**/ /************************************************************************
 * 函数说明: 
 *     骑士knight 从源点(srci,srcj) 走到目的点(desti,destj)
 * 参数说明:
 *     srci  : 源点行下标 (srci>=1 and srci<=8)
 *     srcj  : 源点列下标 (srcj>=1 and srcj<=8)
 *     desti : 目的行下标 (desti>=1 and desti<=8)
 *     destj : 目的列下标 (destj>=1 and destj<=8)
 *     minstep : 从源点到目的点的最短路径步数
 ************************************************************************/
int  knight_walk( int  srci, int  srcj, int  desti, int  destj)
... {
    //初始化棋盘和其他参数
    initialize();

    if(srci==desti && srcj==destj)
        return 0;

    int k=0;    //初始化方向,每个点都从第1个方向开始搜索
    int i,j,newi,newj,step;
    int minstep=MAXMINSTEP;    //当前最短路径

    pathcount=0;
    chess[srci][srcj]=1;
    
    path[0].i=srci;
    path[0].j=srcj;

    step=1;    //先走第一步
    i=srci;
    j=srcj;

    while(step>0)
    ...{
        k++;    //搜索下一个方向

        while(k==9)
        ...{
            //回溯并记录上一步当前出发点
            step--;
            if(step==0)
                break;

            //记录上一步的方向
            k=direction[step];

            //取消上一步到达的点的赋值
            chess[path[step].i][path[step].j]=0;

            i=path[step-1].i;
            j=path[step-1].j;

            //准备搜索下一个方向
            k++;
        }

        if(step==0)
            break;

        //得到新点
        new_point_at_direction(i,j,k,newi,newj);
        //找到一个走后的新点仍在棋盘上的方向
        while(new_point_is_on_chessboard(newi,newj)==false)
        ...{
            k++;    //搜索下一个方向
            if(k==9)
                break;
            new_point_at_direction(i,j,k,newi,newj);
        }

        //8个方向都已经搜索
        if(k==9)
        ...{
            k=8;
            continue;
        }

        //若该点已经访问过
        if(chess[newi][newj]!=0)
            continue;

        //若到达目的点,记录该路径,结束本次搜索,启动下一次搜索
        if(newi==desti && newj==destj)
        ...{
            //记录该步
            direction[step]=k;
            path[step].i=newi;
            path[step].j=newj;

            //记录第pathcount条路径走step步
            pathstep[pathcount++]=step;                    
            chess[newi][newj]=step+1;
            
            /**///////////////////////////////////////////////////////////////////////////            
            //将当前路径存于所有路径数组中
            allpath[pathcount-1].curstep=step;
            for(int m=0;m<=step;m++)
                allpath[pathcount-1].curpath[m]=path[m];
            /**///////////////////////////////////////////////////////////////////////////

            //////////////////////////////////////////////////////////////////////////
            //求当前最短路径
            if(minstep>step)
                minstep=step;
                        
            /**///////////////////////////////////////////////////////////////////////////
            //第1种回溯,回2步
            //该步已经到达,其他的不需要再搜索,只需回溯
            k=direction[step-1];

            //取消上一步到达的点的赋值
            chess[path[step].i][path[step].j]=0;
            chess[path[step-1].i][path[step-1].j]=0;

            //回溯并记录上一步当前出发点
            step--;
            i=path[step-1].i;
            j=path[step-1].j;
            /**///////////////////////////////////////////////////////////////////////////
            
            continue;
        }

        /**///////////////////////////////////////////////////////////////////////////
        //最快的一般不会超过6步,故若在第6步已经试探了所有8个方向还没有到达
        //则回溯,搜索下一个方向,在第6步相当于广度优先搜索
        //即在第6步还有其他方向没有搜索,则继续
        //若求出当前最短路径了,再求出的路径大于此值的路径多可以忽略
        //if(step==MAXMINSTEP)
        if(step==minstep)
            continue;
        /**///////////////////////////////////////////////////////////////////////////

        //记录该步
        direction[step]=k;
        path[step].i=newi;
        path[step].j=newj;

        //记录第step步到达的位置
        i=newi;
        j=newj;
        chess[i][j]=step+1;

        //开始下一步搜索
        step++;
        k=0;
    }

    return minstep;
}

/**/ /************************************************************************
 * 函数说明: 
 *     求最短路径的个数
 * 参数说明:
 *     nMinStep : 最短路径
 * 返回值说明:
 *     nMinStepCount : 最短路径的个数
 ************************************************************************/
int  min_step_count( int  nMinStep)
... {
    int nMinStepCount=0;

    for(int i=0;i<pathcount;i++)
    ...{
        if(pathstep[i]==nMinStep)
            nMinStepCount++;
    }
    return nMinStepCount;
}

// 显示菜单
void  show_menu()
... {
    printf("--------------------------------------------- ");
    printf("input command to test the program ");
    printf("   g or G : get path count (step<=6) ");
    printf("   w or W : get path count and wirte in files ");
    printf("   p or P : test data by input ");
    printf("   q or Q : quit ");
    printf("--------------------------------------------- ");
    printf("$ input command >");
}

/**/ /************************************************************************
 * 函数说明: 
 *     将每一个点到其他64个点路径个数写入文件
 * 参数说明:
 *     srci  : 源点行下标 (srci>=1 and srci<=8)
 *     srcj  : 源点列下标 (srcj>=1 and srcj<=8)
 *     a     : 源点(srci,srcj) 到其他64 个点的路径个数数组
 ************************************************************************/
void  write_path_count( int  srci, int  srcj, int  a[][MAXLENGTH + 1 ])
... {
    FILE *fp;
    char filename[FILENAMELENGTH];
    sprintf(filename,"path number from (%d,%d) to others.txt",srci,srcj);

    fp=fopen(filename,"w");
    if(fp==NULL)
    ...{
        printf("can not wirte file!");
        exit(0);
    }

    for(int i=1;i<=MAXLENGTH;i++)
    ...{
        for(int j=1;j<=MAXLENGTH;j++)
            fprintf(fp,"%-5d",a[i][j]);
        fprintf(fp," ");
    }
    
    fclose(fp);
}

/**/ /************************************************************************
 * 函数说明: 
 *     将每一个点到其他64个点最短路径及其个数写入文件
 * 参数说明:
 *     srci  : 源点行下标 (srci>=1 and srci<=8)
 *     srcj  : 源点列下标 (srcj>=1 and srcj<=8)
 *     aMinStep : 源点(srci,srcj) 到其他64 个点的最短路径数组
 *     aMinStepCount : 源点(srci,srcj) 到其他64 个点的最短路径个数数组
 ************************************************************************/
void  write_min_step_count( int  srci, int  srcj, int  aMinStep[][MAXLENGTH + 1 ],
     int  aMinStepCount[][MAXLENGTH + 1 ])
... {
    FILE *fp;
    char filename[FILENAMELENGTH];
    sprintf(filename,"min step from (%d,%d) to others.txt",srci,srcj);

    fp=fopen(filename,"w");
    if(fp==NULL)
    ...{
        printf("can not wirte file!");
        exit(0);
    }

    //写入提示,(a - b),a 为最短路径,b为最短路径的个数
    fprintf(fp,"(a - b), a is the min step, b is the number of min path ");

    for(int i=1;i<=MAXLENGTH;i++)
    ...{
        for(int j=1;j<=MAXLENGTH;j++)
            fprintf(fp,"(%d - %-3d)  ",aMinStep[i][j],aMinStepCount[i][j]);
        fprintf(fp," ");
    }
    
    fclose(fp);
}

// 计算要搜索的路径个数,求出最短路径个数
void  get_path_count()
... {
    int srci,srcj,desti,destj;
    int minstep;        //最短路径
    int minstepcount;    //最短路径个数

    for(srci=1;srci<=MAXLENGTH;srci++)
    ...{
        for(srcj=1;srcj<=MAXLENGTH;srcj++)
        ...{
            for(desti=1;desti<=MAXLENGTH;desti++)
            ...{
                for(destj=1;destj<=MAXLENGTH;destj++)
                ...{
                    //求(srci,srcj) 到(desti,destj) 最短路径
                    minstep=knight_walk(srci,srcj,desti,destj);

                    //求(srci,srcj) 到(desti,destj) 最短路径的个数
                    minstepcount=min_step_count(minstep);

                    //求要搜索的路径个数最大值
                    if(maxpathcount<pathcount)
                        maxpathcount=pathcount;

                    //求最短路径个数的最大值
                    if(maxminstep<minstepcount)
                        maxminstep=minstepcount;
                }
            }
            printf(".");
        }
    }
    printf(" calculation finished! ");
}

// 计算要搜索的路径个数,求出最短路径个数并写入文件
void  get_and_write_path_count()
... {
    int srci,srcj,desti,destj;
    int minstep;        //最短路径
    int minstepcount;    //最短路径个数

    //所有路径个数
    int aPathCount[MAXLENGTH+1][MAXLENGTH+1]=...{0};

    //最短路径步数
    int aMinStep[MAXLENGTH+1][MAXLENGTH+1]=...{0};

    //最短路径个数
    int aMinStepCount[MAXLENGTH+1][MAXLENGTH+1]=...{0};

    for(srci=1;srci<=MAXLENGTH;srci++)
    ...{
        for(srcj=1;srcj<=MAXLENGTH;srcj++)
        ...{
            for(desti=1;desti<=MAXLENGTH;desti++)
            ...{
                for(destj=1;destj<=MAXLENGTH;destj++)
                ...{
                    //求(srci,srcj) 到(desti,destj) 最短路径
                    minstep=knight_walk(srci,srcj,desti,destj);
                    aPathCount[desti][destj]=pathcount;                    
                    aMinStep[desti][destj]=minstep;

                    //求(srci,srcj) 到(desti,destj) 最短路径的个数
                    minstepcount=min_step_count(minstep);
                    aMinStepCount[desti][destj]=minstepcount;

                    //求要搜索的路径个数最大值
                    if(maxpathcount<pathcount)
                        maxpathcount=pathcount;

                    //求最短路径个数的最大值
                    if(maxminstep<minstepcount)
                        maxminstep=minstepcount;
                }
            }
            //将计算结果写入文件
            write_path_count(srci,srcj,aPathCount);
            write_min_step_count(srci,srcj,aMinStep,aMinStepCount);

            printf(".");
        }
    }
    printf(" calculation finished! ");
}

// 初始化棋盘
void  initialize_chess()
... {
    for(int i=0;i<MAXLENGTH+1;i++)
        for(int j=0;j<MAXLENGTH+1;j++)
            chess[i][j]=0;
}

/**/ /************************************************************************
 * 函数说明: 
 *     输出棋盘上的路径
 * 参数说明:
 *     pathnumber : 路径编号
 *     step       : 第 pathcount 条路径的步数
 ************************************************************************/
void  output_chess( int  pathnumber, int  step)
... {
    printf("path no. = %d, step = %d ",pathnumber,step);
    for(int i=1;i<MAXLENGTH+1;i++)
    ...{
        for(int j=1;j<MAXLENGTH+1;j++)
            printf("%-3d",chess[i][j]);
        printf(" ");
    }
    printf(" ");
}

/**/ /************************************************************************
 * 函数说明: 
 *     输出棋盘上的路径
 * 参数说明:
 *     pathnumber : 路径编号
 *     step       : 第 pathcount 条路径的步数
 *     fp         : 文件指针
 ************************************************************************/
void  output_chess( int  pathnumber, int  step,FILE  * fp)
... {
    fprintf(fp,"path no. = %d, step = %d ",pathnumber,step);
    for(int i=1;i<MAXLENGTH+1;i++)
    ...{
        for(int j=1;j<MAXLENGTH+1;j++)
            fprintf(fp,"%-3d",chess[i][j]);
        fprintf(fp," ");
    }
    fprintf(fp," ");
}

/**/ /************************************************************************
 * 函数说明: 
 *     输出knight 从(srci,srcj) 到(desti,destj) 的所有长度<=6的路径
 * 参数说明:
 *     srci  : 源点行下标 (srci>=1 and srci<=8)
 *     srcj  : 源点列下标 (srcj>=1 and srcj<=8)
 *     desti : 目的行下标 (desti>=1 and desti<=8)
 *     destj : 目的列下标 (destj>=1 and destj<=8)
 *     pathcount : 求源点到目的点间最短路径搜索到的路径个数
 *     nMinStep  : 源点到目的点间最短路径
 *     nMinStepCount : 源点到目的点间最短路径的个数
 ************************************************************************/
void  output_all_path( int  srci, int  srcj, int  desti, int  destj, int  pathcount, int  nMinStep, int  nMinStepCount)
... {
    int step,i,j,curi,curj;
    char filename[FILENAMELENGTH];
    
    //构造文件名
    sprintf(filename,"(%d,%d) to (%d,%d) - all path.txt",srci,srcj,desti,destj);
    FILE *fp=fopen(filename,"w");
    if(fp==NULL)
    ...{
        printf("can not wirte file!");
        exit(0);
    }

    //写入要搜索的路径个数
    fprintf(fp,"(%d,%d) to (%d,%d) path number searched =%d ",srci,srcj,desti,destj,pathcount);

    //写入最短路径及其个数
    fprintf(fp," min step = %d ",nMinStep);
    fprintf(fp," min path number = %d ",nMinStepCount);

    for(curi=0;curi<pathcount;curi++)
    ...{
        //初始化棋盘
        initialize_chess();
        
        step=allpath[curi].curstep;
        for(curj=0;curj<=step;curj++)
        ...{
            //第curi条路径的第curj步的行、列下标
            i=allpath[curi].curpath[curj].i;
            j=allpath[curi].curpath[curj].j;
            //给棋盘赋值
            chess[i][j]=curj+1;
        }

        //输出棋盘到屏幕
        output_chess(curi+1,step);

        //输出棋盘到文件
        output_chess(curi+1,step,fp);
    }

    fclose(fp);
}

/**/ /************************************************************************
 * 函数说明: 
 *     输出knight 从(srci,srcj) 到(desti,destj) 的最短路径
 * 参数说明:
 *     srci  : 源点行下标 (srci>=1 and srci<=8)
 *     srcj  : 源点列下标 (srcj>=1 and srcj<=8)
 *     desti : 目的行下标 (desti>=1 and desti<=8)
 *     destj : 目的列下标 (destj>=1 and destj<=8)
 *     pathcount : 求源点到目的点间最短路径搜索到的路径个数
 *     nMinStep  : 源点到目的点间最短路径
 *     nMinStepCount : 源点到目的点间最短路径的个数
 ************************************************************************/
void  output_min_path( int  srci, int  srcj, int  desti, int  destj, int  pathcount, int  nMinStep, int  nMinStepCount)
... {
    int step,i,j,curi,curj;
    char filename[FILENAMELENGTH];
    
    //构造文件名
    sprintf(filename,"(%d,%d) to (%d,%d) - min path.txt",srci,srcj,desti,destj);
    FILE *fp=fopen(filename,"w");
    if(fp==NULL)
    ...{
        printf("can not wirte file!");
        exit(0);
    }

    //写入最短路径及其个数
    fprintf(fp,"(%d,%d) to (%d,%d) min step = %d ",srci,srcj,desti,destj,nMinStep);
    fprintf(fp," min path number = %d ",nMinStepCount);

    for(curi=0;curi<pathcount;curi++)
    ...{
        step=allpath[curi].curstep;

        if(step!=nMinStep)
            continue;

        //初始化棋盘
        initialize_chess();

        for(curj=0;curj<=step;curj++)
        ...{
            //第curi条路径的第curj步的行、列下标
            i=allpath[curi].curpath[curj].i;
            j=allpath[curi].curpath[curj].j;
            //给棋盘赋值
            chess[i][j]=curj+1;
        }

        //输出棋盘到屏幕
        output_chess(curi+1,step);

        //输出棋盘到文件
        output_chess(curi+1,step,fp);
    }

    fclose(fp);
}

main()
... {
    int srcrow,srccol,destrow,destcol;
    char sinput[10];

    show_menu();

    scanf("%s",sinput);
    while(stricmp(sinput,"q")!=0)
    ...{
        if(stricmp(sinput,"p")==0)
        ...{
            printf("$ input src point :  col(a~h) >");
            scanf("%s",sinput);                
            srccol=sinput[0]-96;

            printf("$ input src point :  row(1~8) >");
            scanf("%d",&srcrow);

            printf("$ input dest point : col(a~h) >");
            scanf("%s",sinput);
            destcol=sinput[0]-96;

            printf("$ input dest point : row(1~8) >");
            scanf("%d",&destrow);

            //求解
            int nMinStep=knight_walk(srcrow,srccol,destrow,destcol);
            int nMinStepCount=min_step_count(nMinStep);

            //显示最短路径
            printf(" %c%d to %c%d : min step = %d ",srccol+96,srcrow,destcol+96,destrow,nMinStep);
            
            //显示要搜索的路径个数及其最短路径个数
            printf("path number searched =%d, min path number = %d ",pathcount,nMinStepCount);            

            printf("$ display All searched path,Min path or Return (A,M,R)? >");
            scanf("%s",sinput);
            while(stricmp(sinput,"r")!=0)
            ...{
                if(stricmp(sinput,"a")==0)        //显示所有路径
                ...{
                    //输出所有路径
                    output_all_path(srcrow,srccol,destrow,destcol,pathcount,nMinStep,nMinStepCount);

                    //输入命令
                    printf("$ display All searched path,Min path or Return (A,M,R)? >");
                    scanf("%s",sinput);
                }
                else if(stricmp(sinput,"m")==0)    //显示最短路径
                ...{
                    //输出最短路径
                    output_min_path(srcrow,srccol,destrow,destcol,pathcount,nMinStep,nMinStepCount);

                    //输入命令
                    printf("$ display All searched path,Min path or Return (A,M,R)? >");
                    scanf("%s",sinput);
                }
                else if(stricmp(sinput,"r")==0)
                    break;
            }
        }
        else if(stricmp(sinput,"g")==0)
        ...{
            //得到所有任意两点间路径个数
            get_path_count();

            printf("max path number searched of all two points: %d ",maxpathcount);
            printf("max path number of all min step count : %d ",maxminstep);
        }
        else if(stricmp(sinput,"w")==0)
        ...{
            //得到所有任意两点间路径个数并写入文件
            get_and_write_path_count();

            printf("max path number searched of all two points: %d ",maxpathcount);
            printf("max path number of all min step count : %d ",maxminstep);
        }

        //输入命令
        printf("$ input command >");
        scanf("%s",sinput);
    }

    return 0;
}

 

运行结果如下：

 

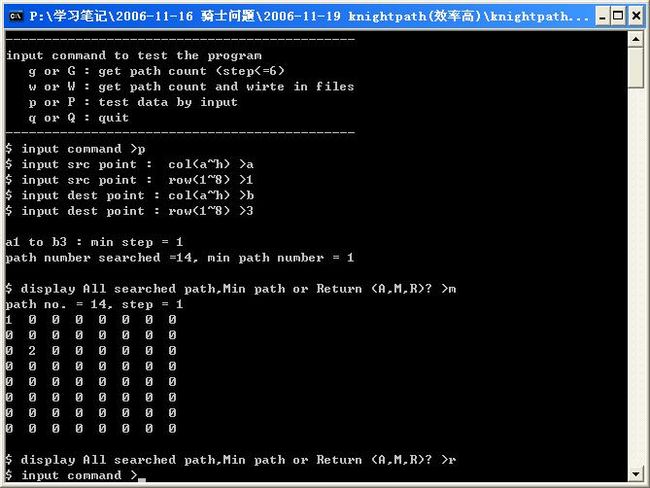
文件内容解释说明：

例如，文件“(1,1) to (2,2) - all path.txt”表示通过本算法找到的点(1,1)到点(2,2)间的所有路径，共搜索到19条路径，其中最短路径10条，其最短步长为4。

(1,1) to (2,2)
        path number searched =19
        min step = 4
        min path number = 10

path no. = 1, step = 6
1  0  0  0  3  0  0  0 
0  7  2  0  0  0  4  0 
0  0  0  6  0  0  0  0 
0  0  0  0  0  5  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 2, step = 6
1  0  0  0  3  0  0  0 
0  7  2  0  0  0  4  0 
0  0  0  0  5  0  0  0 
0  0  6  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 3, step = 6
1  0  0  6  3  0  0  0 
0  7  2  0  0  0  4  0 
0  0  0  0  5  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 4, step = 6
1  0  0  0  3  0  0  0 
0  7  2  0  0  0  0  0 
0  0  0  0  0  4  0  0 
0  0  6  0  0  0  0  0 
0  0  0  0  5  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 5, step = 6
1  0  0  0  3  0  0  0 
0  7  2  0  0  0  0  0 
0  0  0  6  0  4  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  5  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 6, step = 6
1  0  0  0  3  0  0  0 
0  7  2  5  0  0  0  0 
0  0  0  0  0  4  0  0 
0  0  6  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 7, step = 6
1  0  0  6  3  0  0  0 
0  7  2  0  0  5  0  0 
0  0  0  4  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 8, step = 6
1  0  0  0  3  0  0  0 
0  7  2  0  0  0  0  0 
0  0  0  4  0  0  0  0 
0  0  6  0  0  0  0  0 
0  0  0  0  5  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 9, step = 6
1  0  0  0  3  0  0  0 
0  7  2  0  0  0  0  0 
0  0  0  4  0  0  0  0 
6  0  0  0  0  0  0  0 
0  0  5  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 10, step = 4
1  0  0  0  3  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  4  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 11, step = 4
1  0  0  0  0  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  0  3  0  0  0 
0  0  4  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 12, step = 4
1  0  0  4  0  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  0  3  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 13, step = 4
1  0  0  0  0  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  4  0  0  0  0 
0  3  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 14, step = 4
1  0  0  0  0  0  0  0 
0  5  2  0  0  0  0  0 
3  0  0  0  0  0  0  0 
0  0  4  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 15, step = 4
1  0  3  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  4  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 16, step = 4
1  0  0  0  0  0  0  0 
0  5  0  3  0  0  0  0 
0  2  0  0  0  0  0  0 
0  0  4  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 17, step = 4
1  0  0  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  4  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  3  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 18, step = 4
1  0  0  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  0  0  0  0  0 
4  0  0  0  0  0  0  0 
0  0  3  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 19, step = 4
1  0  0  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  0  0  0  0  0 
0  0  4  0  0  0  0  0 
3  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

例如，文件“(1,1) to (2,2) - min path.txt”记录点(1,1)到点(2,2)间的所有最短路径。

(1,1) to (2,2)
           min step = 4
           min path number = 10

path no. = 10, step = 4
1  0  0  0  3  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  4  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 11, step = 4
1  0  0  0  0  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  0  3  0  0  0 
0  0  4  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 12, step = 4
1  0  0  4  0  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  0  3  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 13, step = 4
1  0  0  0  0  0  0  0 
0  5  2  0  0  0  0  0 
0  0  0  4  0  0  0  0 
0  3  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 14, step = 4
1  0  0  0  0  0  0  0 
0  5  2  0  0  0  0  0 
3  0  0  0  0  0  0  0 
0  0  4  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 15, step = 4
1  0  3  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  4  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 16, step = 4
1  0  0  0  0  0  0  0 
0  5  0  3  0  0  0  0 
0  2  0  0  0  0  0  0 
0  0  4  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 17, step = 4
1  0  0  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  4  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  3  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 18, step = 4
1  0  0  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  0  0  0  0  0 
4  0  0  0  0  0  0  0 
0  0  3  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 

path no. = 19, step = 4
1  0  0  0  0  0  0  0 
0  5  0  0  0  0  0  0 
0  2  0  0  0  0  0  0 
0  0  4  0  0  0  0  0 
3  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0 
0  0  0  0  0  0  0  0