用C++实现一个Quaternion类
提要
四元素是游戏开发中常用的用于处理旋转的数学工具,下面就用C++来实现一个四元素类。参考Unity中四元素的接口。
如果没有看之前的 彻底搞懂四元数, 建议先看一下。
代码清单
Quaternion.h
#pragma once
#include "Vector3.h"
#include "Mathf.h"
class Quaternion
{
public:
Quaternion(float x, float y, float z, float w);
Quaternion(float yaw, float pitch, float roll);
~Quaternion();
static Quaternion identity;
static float Dot(const Quaternion &lhs, const Quaternion &rhs);
static Quaternion Lerp(const Quaternion &a, const Quaternion &b, float t);
static Quaternion Slerp(const Quaternion &a, const Quaternion &b, float t);
static float Angle(const Quaternion &lhs, const Quaternion &rhs);
void SetEulerAngle(float yaw, float pitch, float roll);
void Set(float _x, float _y, float _z, float _w);
Quaternion Conjugate() const;
Quaternion Inverse() const;
Vector3 EulerAngle() const;
void operator+(const Quaternion &q);
void operator*(float s);
void operator-(const Quaternion &q);
friend Quaternion operator * (const Quaternion& lhs, const Quaternion& rhs);
friend Vector3 operator *(const Quaternion& rotation, const Vector3& point);
float x;
float y;
float z;
float w;
private:
Vector3 eulerAngles;
};
Quaternion.cpp
#include "Quaternion.h"
Quaternion Quaternion::identity(0, 0, 0, 1);
Quaternion::Quaternion(float _x, float _y, float _z, float _w)
{
float mag = _x *_x + _y*_y + _z *_z + _w*_w;
x = _x / mag;
y = _y / mag;
z = _z / mag;
w = _w / mag;
}
Quaternion::Quaternion(float yaw, float pitch, float roll)
{
this->SetEulerAngle(yaw, pitch, roll);
}
Quaternion::~Quaternion()
{
}
//Cos theta of two quaternion
float Quaternion::Dot(const Quaternion &lhs, const Quaternion &rhs)
{
return lhs.x * rhs.x + lhs.y * rhs.y + lhs.z * rhs.z + lhs.w * rhs.w;
}
Quaternion Quaternion::Slerp(const Quaternion &a, const Quaternion &b, float t)
{
float cos_theta = Dot(a, b);
// if B is on opposite hemisphere from A, use -B instead
float sign;
if (cos_theta < 0.f)
{
cos_theta = -cos_theta;
sign = -1.f;
}
else sign = 1.f;
float c1, c2;
if (cos_theta > 1.f - Mathf::EPSILON)
{
// if q2 is (within precision limits) the same as q1,
// just linear interpolate between A and B.
c2 = t;
c1 = 1.f - t;
}
else
{
//float theta = gFloat::ArcCosTable(cos_theta);
// faster than table-based :
//const float theta = myacos(cos_theta);
float theta = acos(cos_theta);
float sin_theta = sin(theta);
float t_theta = t*theta;
float inv_sin_theta = 1.f / sin_theta;
c2 = sin(t_theta) * inv_sin_theta;
c1 = sin(theta - t_theta) * inv_sin_theta;
}
c2 *= sign; // or c1 *= sign
// just affects the overrall sign of the output
// interpolate
return Quaternion(a.x * c1 + b.x * c2, a.y * c1 + b.y * c2, a.z * c1 + b.z * c2, a.w * c1 + b.w * c2);
}
Quaternion Quaternion::Lerp(const Quaternion &a, const Quaternion &b, float t)
{
return Quaternion((1 - t) * a.x + t * b.x,
(1 - t) * a.y + t * b.y,
(1 - t) * a.z + t * b.z,
(1 - t) * a.w + t * b.w);
}
float Quaternion::Angle(const Quaternion &lhs, const Quaternion &rhs)
{
float cos_theta = Dot(lhs, rhs);
// if B is on opposite hemisphere from A, use -B instead
if (cos_theta < 0.f)
{
cos_theta = -cos_theta;
}
float theta = acos(cos_theta);
return 2 * Mathf::Rad2Deg * theta;
}
void Quaternion::Set(float _x, float _y, float _z, float _w)
{
x = _x;
y = _y;
z = _z;
w = _w;
}
void Quaternion::SetEulerAngle(float yaw, float pitch, float roll)
{
float angle;
float sinRoll, sinPitch, sinYaw, cosRoll, cosPitch, cosYaw;
angle = yaw * 0.5f;
sinYaw = sin(angle);
cosYaw = cos(angle);
angle = pitch * 0.5f;
sinPitch = sin(angle);
cosPitch = cos(angle);
angle = roll * 0.5f;
sinRoll = sin(angle);
cosRoll = cos(angle);
float _y = cosRoll*sinPitch*cosYaw + sinRoll*cosPitch*sinYaw;
float _x = cosRoll*cosPitch*sinYaw - sinRoll*sinPitch*cosYaw;
float _z = sinRoll*cosPitch*cosYaw - cosRoll*sinPitch*sinYaw;
float _w = cosRoll*cosPitch*cosYaw + sinRoll*sinPitch*sinYaw;
float mag = _x *_x + _y*_y + _z *_z + _w*_w;
x = _x / mag;
y = _y / mag;
z = _z / mag;
w = _w / mag;
}
void Quaternion::operator+(const Quaternion &q)
{
x += q.x;
y += q.y;
z += q.z;
w += q.w;
}
void Quaternion::operator-(const Quaternion &q)
{
x -= q.x;
y -= q.y;
z -= q.z;
w -= q.w;
}
void Quaternion::operator*(float s)
{
x *= s;
y *= s;
z *= s;
w *= s;
}
Quaternion Quaternion::Conjugate() const
{
return Quaternion(-x, -y, -z, w);
}
Quaternion Quaternion::Inverse() const
{
return Quaternion(-x, -y, -z, w);
}
Quaternion operator * (const Quaternion& lhs, const Quaternion& rhs)
{
float w1 = lhs.w;
float w2 = rhs.w;
Vector3 v1(lhs.x, lhs.y, lhs.z);
Vector3 v2(rhs.x, rhs.y, rhs.z);
float w3 = w1 * w2 - Vector3::Dot(v1, v2);
Vector3 v3 = Vector3::Cross(v1, v2) + w1 * v2 + w2 * v1;
return Quaternion(v3.x, v3.y, v3.z, w3);
}
Vector3 operator *(const Quaternion& q, const Vector3& v)
{
/*
Quaternion tmp(v.x, v.y, v.z, 0); //This will normalise the quaternion. this will case error.
Quaternion result = q * tmp * q.Conjugate();
return Vector3(result.x, result.y, result.z);*/
// Extract the vector part of the quaternion
Vector3 u(q.x, q.y, q.z);
// Extract the scalar part of the quaternion
float s = q.w;
// Do the math
return 2.0f * Vector3::Dot(u, v) * u
+ (s*s - Vector3::Dot(u, u)) * v
+ 2.0f * s * Vector3::Cross(u, v);
}
Vector3 Quaternion::EulerAngle() const
{
float yaw = atan2(2 * (w * x + z * y), 1 - 2 * (x * x + y * y));
float pitch = asin(Mathf::Clamp(2 * (w * y - x * z), -1.0f, 1.0f));
float roll = atan2(2 * (w * z + x * y), 1 - 2 * (z * z + y * y));
return Vector3(Mathf::Rad2Deg * yaw, Mathf::Rad2Deg * pitch, Mathf::Rad2Deg * roll);
}
测试
void QuaternionTest()
{
qDebug() << Mathf::Rad2Deg * Mathf::Pi * 0.25f;// 45
qDebug() << Mathf::Deg2Rad * 45;// 0.785398163397
Quaternion a = Quaternion::identity;
Quaternion b(Mathf::Pi * 0.5, 0, 0);
qDebug() << "a" << a << a.EulerAngle();
qDebug() << "b" << b << b.EulerAngle();
qDebug() << Quaternion::Angle(a, b);
Quaternion c = Quaternion::Slerp(a, b, 0.5f);
qDebug() <<"c" <<c << c.EulerAngle();
qDebug() << Quaternion::Angle(a, c);
Quaternion d = b * c;
qDebug() << "d" << d << d.EulerAngle();
Vector3 pos(1, 2, 3);
qDebug() << "c * (1, 2, 3) "<<c * pos;
}
运行结果
关于四元素和Vector3乘法的优化
四元素和向量相乘最容易用到的应该是骨骼动画,计算量是非常大的,所以对四元素和向量相乘的算法可以设法优化一下。
对于向量 v 和 四元素 q,最原始的乘法是这样的。
1) Create a pure quaternion p out of v. This simply means adding a fourth coordinate of 0:![]()
2) Pre-multiply it with q and post-multiply it with the conjugate q*:
![]()
3) This will result in another pure quaternion which can be turned back to a vector:![]()
This vector v' is v rotated by q.
一个优化的算法是这样的
We can also describe q as the combination of a 3-dimensional vector u and a scalar s:
![]()
By the rules of quaternion multiplication, and as the conjugate of a unit length quaternion is simply it's inverse, we get:
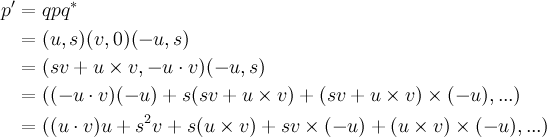
this is very long to re-type
The scalar part (ellipses) results in zero, as detailed here. What's interesting is the vector part, AKA our rotated vector v'. It can be simplified using some basic vector identities:
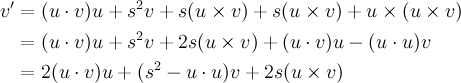
that too
This is now much more optimal; two dot products, a cross product and a few extras: around half the operations.
代码可以写成这样
void rotate_vector_by_quaternion(const Vector3& v, const Quaternion& q, Vector3& vprime)
{
// Extract the vector part of the quaternion
Vector3 u(q.x, q.y, q.z);
// Extract the scalar part of the quaternion
float s = q.w;
// Do the math
vprime = 2.0f * dot(u, v) * u
+ (s*s - dot(u, u)) * v
+ 2.0f * s * cross(u, v);
}
这样写不仅非常清晰,而且有个哥们用sse优化之后,竟然有35% faster。
参考
Understanding Quaternions - http://blog.csdn.net/silangquan/article/details/39008903
A faster quaternion-vector multiplication - http://blog.molecular-matters.com/2013/05/24/a-faster-quaternion-vector-multiplication/
Rotating vector3 by a quaternion - http://gamedev.stackexchange.com/questions/28395/rotating-vector3-by-a-quaternion
