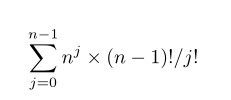第二届华中区程序设计邀请赛暨武汉大学第十一届校赛 现场赛 解题报告
The 11thWuhan University
The 2rdCentral China Invitation
ProgrammingContest
Solution
Problem A: All Your Bases
Problem B: Beautiful Cities
Problem C: Check the Identity
Problem D: Demon Tour
Problem E: Enthusiasts
Problem F: Game
Problem G: Hunan Restaurant
Problem H: Key Logger
Problem I: Longest Lane
Problem J: Two Strings
April 23rd, 2013 by chlxyd
Problem A: All Your Bases(H)
Time Limit: 10 s
给一颗n个点的树,边上有权值,有t个关键点,删去k条边,原树变为k+1部分,问每部分均有至少一个关键点的最小删边费用。
Solution
Tag:图论
把n-1条边按从大到小排序,维护一个并查集,如果发现当前边连接的两个集合均有关键点,那么看当前关键点数量是否大于t,如果大于就合并,否则就认为要删该条边,加入到答案中;如果当前边连接的两个集合不是均有关键点,那么直接合并。复杂度O(n)。
/*
* Author: chlxyd
* Created Time: 2013/4/22 23:31:21
* File Name: A.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
int T , n , t , k ;
struct vtype{
int a , b , c ;
bool operator < ( const vtype & q ) const {
return c < q.c ;
}
}v[20000] ;
int f[20000] ;
bool bj[20000] ;
int find( int x ) {
if ( f[x] == x ) return x ;
return f[x] = find(f[x]) ;
}
int main(){
scanf("%d" , &T ) ;
int ca = 0 ;
while ( scanf("%d %d %d" , &n , &t , &k ) == 3 ) {
clr(bj) ; k ++ ;
repf( i , 1 , n - 1 )
scanf("%d %d %d" , &v[i].a , &v[i].b , &v[i].c ) ;
sort( v+1 , v+n ) ;
repf( i , 1 , n ) f[i] = i ;
repf( i , 1 , t ) {
int x ;
scanf("%d" , &x );
bj[x] = true ;
}
int ans = 0 , have = t ;
repd( i , n - 1 , 1 ) {
int a = v[i].a , b = v[i].b , c = v[i].c ;
a = find(a) , b = find(b) ;
if ( bj[a] && bj[b] ) {
if ( have > k ) {
have -- ;
f[a] = b ;
}
else ans += c ;
}
else {
f[a] = b ;
bj[b] = bj[b] | bj[a] ;
}
}
printf("Case %d: %d\n" , ++ca , ans ) ;
}
}
ProblemB: Beautiful Cities(H)
Time Limit: 3 s
给n个点,每个点都向其余n-1个顶点中某一个连一条无向边(也可以不连),问原图连通的方案数。
Solution
Tag:图论,数学
purfer编码,首先枚举环的长度,设为n-j,然后还剩下j个点,会形成一个长度为j的purfer码序列,要保证最后能连在环上,序列的最后一位必然为环上的某一个点,那么对于该长度环,方案数为![]() ,化简即可得上述结果。
,化简即可得上述结果。
/*
* Author: chlxyd
* Created Time: 2013/4/22 23:15:33
* File Name: B.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (long long i = 0; i < (n); ++i)
#define repf(i, a, b) for (long long i = (a); i <= (b); ++i)
#define repd(i, a, b) for (long long i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
#define mod 1000000007
long long n , T , ca ;
long long a[50000] , b[50000] ;
int main(){
scanf("%lld" , &T ) ;
while ( scanf("%lld" , &n ) == 1 ) {
long long ans = 0 ;
a[0] = 1 ; b[n-1] = 1 ;
repf( i , 1 , n - 1 ) a[i] = a[i-1] * n % mod ;
repd( i , n - 2 , 0 ) b[i] = b[i+1] * ( i + 1 ) % mod ;
repf( i , 0 , n - 1 ) {
ans = ans + a[i] * b[i] % mod ;
ans %= mod ;
}
printf("Case %lld: %lld\n" , ++ca , ans ) ;
}
}
Problem C: Check the Identity(N)
Time Limit: 10 s
一个有sin,cos,tan,+,-,*,x的后缀表达式,问是否对于所有的x值均为0。
Solution
Tag:乱搞,数据结构
题目的想法还是很简单的,就是随机好多好多x然后去试就完了,当x数量足够多的时候,基本上构造不出什么数据来cha掉。
那么为什么那么多队伍在比赛的时候挂掉了?
关键就在于tan运算,当tan的值非常接近π/2的倍数的时候,就会产生一个非常大的数,如果这样两个一样的数相减的话,虽然答案肯定为0,但是因为实数处理的误差,最后的结果很有可能不为0,导致错误的判断。所以很多队伍一开始交了挂了,然后以为随机的不够多,去随机更多的试,于是随机的越多就越可能产生π/2的倍数的中间结果,越有可能过不了。
所以要通过该题,做法有两种:1.随机非常少的数(比赛的时候有一只队伍define了一个x然后过了我会乱说。。)2.随机很多数,当发现某组要tan的数很接近π/2的时候,直接返回true,放弃该组。
/*
* Author: chlxyd
* Created Time: 2013/4/19 19:02:00
* File Name: C.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
char s[1000][10] ;
int n ;
double now ;
stack<double> st ;
int sgn( double x ){
return ( x > eps ) - ( x < - eps ) ;
}
bool cal( double now ) {
while ( !st.empty() ) st.pop() ;
repf( i , 1 , n ) {
if ( s[i][0] == 'x' ) st.push(now) ;
else if ( s[i][0] == 's' ) {
double v = st.top() ; st.pop() ;
v = sin(v) ; st.push(v) ;
}
else if ( s[i][0] == 'c' ) {
double v = st.top() ; st.pop() ;
v = cos(v) ; st.push(v) ;
}
else if ( s[i][0] == 't' ) {
double v = st.top() ; st.pop() ;
if ( min( abs(fmod( v , acos(-1.0)/2)) , acos(-1.0)/2 - abs(fmod( v , acos(-1.0)/2)) ) <= 0.01 ) return true ;
v = tan(v) ; st.push(v) ;
}
else if ( s[i][0] == '-' ) {
double a = st.top() ; st.pop() ;
double b = st.top() ; st.pop() ;
st.push(b-a) ;
}
else if ( s[i][0] == '+' ) {
double a = st.top() ; st.pop() ;
double b = st.top() ; st.pop() ;
st.push(b+a) ;
}
else if ( s[i][0] == '*' ) {
double a = st.top() ; st.pop() ;
double b = st.top() ; st.pop() ;
st.push(b*a) ;
}
}
return sgn( st.top() ) == 0 ;
}
int main(){
//freopen("C.in","r",stdin) ;
srand(time(NULL));
int step = 10000 ;
double ste = 2 * acos(-1.0) / step ;
int T ;
int ca = 0 ;
scanf("%d" , &T ) ;
//freopen("C.OUT","w",stdout);
while ( T -- ) {
now = 0 ;
scanf("%d" , &n ) ;
repf( i , 1 , n )
scanf("%s" , s[i] ) ;
int ans = true ;
repf( i , 1 , step ) {
ans = ans & cal( now ) ;
now += ste ;
if ( !ans ) break ;
}
repf( i , 1 , 10000 ) {
double now = 2 * acos(-1.0) * ( rand() + 1 ) / RAND_MAX ;
ans = ans & cal(now) ;
//cout<<now<<endl;
if ( !ans ) break ;
}
printf("Case %d: %s\n" , ++ca , ans?"Yes":"No") ;
}
}
Problem D: Demon Tour(VH)
Time Limit: 10 s
有13个点,然后78条必然要经过的路,200条可以经过的路,路都有代价,问从1出发,经过所有要经过的路回到1的最小花费,没有自环。
PS:红色部分为现场赛题目的疏漏,非常抱歉。
Solution
Tag:动态规划,图论
.首先把必须走的路连通。
1.这些路的端点(包括1)全在一个连通分量内,那么我们可以得到每个顶点的度的奇偶序列,根据欧拉回路的性质,我们可以利用集合DP来推导出所有顶点度均为偶数的最小代价。
2.如果这些路的端点(包括1)不在一个连通分量内,那么原图最多被分为7个连通块(单点除了1其余不用考虑),可以利用集合DP求出使这7个连通块连通的最小代价以及最后节点的奇偶状态,然后再通过一次前面的集合DP即可推导出所有点度数均为偶数的最小花费。
具体见代码。
/*
* Author: chlxyd
* Created Time: 2013/4/22 23:58:45
* File Name: D.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
int n , m , num ;
int g[20][20] ;
int vis[20] ;
int val[1<<14] ;
int dp[1<<7][1<<14] ;
int T , ans ;
void dfs( int i , int block ) {
if ( vis[i] != -1 ) return ;
vis[i] = block ; num ++ ;
repf( j , 1 , n )
if ( g[i][j] != 30000000 )
dfs( j , block ) ;
}
int main(){
//freopen("D1.in","r",stdin) ;
scanf("%d" , &T ) ;
int ca = 0 ;
while ( scanf("%d %d" , &n , &m ) == 2 ) {
repf( i , 1 , n )
repf( j , 1 , n )
g[i][j] = 30000000 ;
int t = 0 ;
ans = 0 ;
repf( i , 1 , m ) {
int a , b , c ;
scanf("%d %d %d" , &a , &b , &c ) ;
ans += c ;
g[a][b] = g[b][a] = c ;
t ^= (1<<(a-1))^(1<<(b-1)) ;
}
int block = -1 ; clrs(vis,-1) ;
repf( i , 1 , n )
if ( vis[i] == -1 ) {
num = 0 ;
dfs(i,++block) ;
if ( num == 1 && i != 1 ) {
vis[i] = -1 ; block -- ;
}
}
block ++ ;
scanf("%d" , &m ) ;
repf( i , 1 , m ) {
int a , b , c ;
scanf("%d %d %d" , &a , &b , &c ) ;
g[a][b] = g[b][a] = min( g[a][b] , c ) ;
}
repf( k , 1 , n )
repf( i , 1 , n )
repf( j , 1 , n )
if ( i != j && i != k && j != k )
if ( g[i][j] > g[i][k] + g[k][j] )
g[i][j] = g[i][k] + g[k][j] ;
rep( i , 1 << block )
rep( j , 1 << n )
dp[i][j] = 30000000 ;
rep( i , block ) dp[(1<<i)][t] = 0 ;
rep( i , 1 << block )
rep( j , 1 << n )
repf( x , 1 , n ) {
if ( vis[x] == -1 ) continue ;
if ( i & ( 1 << ( vis[x] ) ) ) {
repf( y , 1 , n )
if ( vis[y] != -1 && vis[y] != vis[x] && g[x][y] && ( i && ( 1 << vis[y] ) ) )
dp[i][j] = min( dp[i][j] , dp[i^(1<<vis[y])][j^(1<<(y-1))^(1<<(x-1))] + g[x][y] ) ;
}
}
rep( i , 1 << n ) val[i] = dp[(1<<block)-1][i] ;
repd( i , ( 1 << n ) - 1 , 0 )
repf( j , 1 , n )
if ( !( i & ( 1 << (j-1) ) ) )
repf( k , 1 , n )
if ( !( i & ( 1 << (k-1) ) ) )
val[i] = min( val[i] , val[i^(1<<(k-1))^(1<<(j-1))] + g[j][k] ) ;
printf("Case %d: %d\n" , ++ca , val[0] + ans ) ;
}
}
Problem E: Enthusiast(E)
Time Limit: 3 s
问一个歌曲序列出现的概率。
Solution
Tag:数学
签到题,歌曲序列是眼子,直接无视就好了,公式(1/n)^m。
/*
* Author: chlxyd
* Created Time: 2013/4/22 21:09:24
* File Name: E.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
int main(){
int T , n , m ;
scanf("%d" , &T ) ;
repf ( ca , 1 , T ) {
scanf("%d %d\n" , &n , &m ) ;
char s[1000] ;
repf( i , 1 , n + m ) gets(s) ;
printf("Case %d: %.6lf\n" , ca , pow(1.0/n,m*1.0) ) ;
}
}
Problem F: Game(N)
Time Limit: 10 s
一个n*n的矩阵,有的已经被占,每次选水平的两个空的隔一个的格子,然后均占据,两人轮流操作,谁不能操作谁就输,问先手是否必胜。
Solution
Tag:博弈
首先每行是可以单独考虑的,然后奇数列和偶数列也是可以单独考虑的,对于奇数列或者偶数列,被隔开的部分也是可以单独考虑的,那么问题转化成:一个长为n的空格子,每次选相邻两个占据,两人轮流操作,问先手是否必胜。
那么就是个很裸的分堆SG问题了,枚举当前手可选的操作位置,那么分开的两堆的sg值异或起来就是当前一个能到达的局面,不能到达的最小的值即为当前局面的sg值,最后根据sg值是否为0就知道是否先手必胜了。
把sg值预处理出来,对于每个分开的部分直接查表然后异或起来就可以了。复杂度O(N*N)。
/*
* Author: chlxyd
* Created Time: 2013/4/18 17:56:29
* File Name: SG.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
set<int> st ;
int sg[2000] ;
int n ;
int a[2] ;
int main(){
sg[0] = 0 ; sg[1] = 0 ;
repf( i , 2 , 1000 ) {
st.clear() ;
repf( j , 1 , i - 1 )
st.insert( sg[j-1] ^ sg[i-j-1] ) ;
repf( j , 0 , i )
if ( st.find(j) == st.end() ) {
sg[i] = j ;
break ;
}
}
//freopen("sg.in","r",stdin) ;
//freopen("sg.out","w",stdout) ;
int T ;
scanf("%d" ,& T ) ;
int ca = 0 ;
while ( scanf("%d" , &n ) == 1 ) {
int ans = 0 ;
repf( i , 1 , n ) {
a[0] = a[1] = 0 ;
repf( j , 1 , n ) {
int x ;
scanf("%d" , &x ) ;
if ( x == 0 ) a[j%2] ++ ;
else {
ans ^= sg[a[j%2]] ;
a[j%2] = 0 ;
}
}
repf( j , 0 , 1 ) {
ans ^= sg[a[j]] ;
a[j] = 0 ;
}
}
printf("Case %d: %s\n" , ++ca , ans ? "Alice" : "Bob" ) ;
}
}
Problem G: Hunan Restaurant(N)
Time Limit: 3 s
PS:目测这道题和C题一起奠定了比赛的坑爹节奏。
题意比较繁琐,不赘述了,大家耐着性子慢慢看就好。
Solution
Tag:贪心,模拟
这道题本来是除了E和J之外的第三板刷题的定位,不过最开始有只队伍很快过了C,然后大家都去搞C去了,C的trick又非常难想到,于是很多人就被C卡的意识模糊了,加上这道题题面很长,目测好多队伍根本连看都没看,然后这么一道板刷题居然沦落到了只有岛娘一只队伍过的囧况(PS:还是绝杀)。
做法非常简单,对于每桌的菜肯定是先上做的时间少的,然后序列确定了顺次模拟一下就好了。
/*
* Author: chlxyd
* Created Time: 2013/4/19 17:02:58
* File Name: Hunan.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
multiset<int> st[50] ;
multiset<int>::iterator x[50] ;
vector<int> num[50] ;
int n , m , T ;
int t[50] ;
int cal( int i ) {
int now = 0 , ret = 0 ;
rep( j , num[i].size() ) {
ret += num[i][j] <= now ? 0 : num[i][j] - now ;
now = max( now , num[i][j] + 20 ) ;
}
return ret ;
}
int main(){
//freopen("Hunan.out","w",stdout) ;
scanf("%d" , &T ) ;
int ca = 0 ;
while ( scanf("%d %d" , &n , &m ) == 2 ) {
repf ( i , 1 , n ) {
st[i].clear() ;
num[i].clear() ;
}
repf( j , 1 , m )
scanf( "%d" , &t[j] ) ;
repf( i , 1 , n ) {
int k ;
scanf("%d" , &k ) ;
repf( j , 1 , k ) {
int a ;
scanf("%d" , &a ) ;
st[i].insert( t[a] ) ;
}
}
repf( i , 1 , n ) x[i] = st[i].begin() ;
int now = 0 ;
repf( i , 1 , 20 ) {
repf( j , 1 , n ) {
if ( x[j] == st[j].end() ) continue ;
now += *x[j] ;
num[j].push_back(now) ;
x[j] ++ ;
}
}
int ans = 0 ;
repf( i , 1 , n )
ans += cal(i) ;
printf("Case %d: %d\n" , ++ca , ans ) ;
}
}
Problem H: Key Logger(N)
Time Limit: 3 s
3种操作,一种左右移动光标,一种删除当前光标位置的字符,一种输入一个字符在当前光标位置。问最后的输出序列。
Solution
Tag:数据结构,模拟
符合o(1)移动位置,o(1)插入,o(1)删除的数据结构就是链表了吧。。
然后拿个list或者开个链表模拟就好。
/*
* Author: chlxyd
* Created Time: 2013/4/22 22:20:45
* File Name: H.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
struct str {
list<char> s ;
list<char>::iterator x ;
void clear() {
s.clear() ;
x = s.end() ;
}
void movef() {
if ( x == s.begin() ) return ;
x -- ;
}
void moveb() {
if ( x == s.end() ) return ;
x ++ ;
}
void del() {
if ( x == s.begin() ) return ;
x -- ;
x = s.erase(x) ;
}
void insert( char c ) {
s.insert(x,c) ;
}
string show() {
string ret = "" ;
list<char>::iterator d ;
for ( d = s.begin() ; d != s.end() ; d ++ )
ret += *d ;
return ret ;
}
}mystr ;
char ss[1100000] ;
int main(){
int T ;
int ca = 0 ;
scanf("%d" , &T ) ;
while ( scanf("%s" , ss ) == 1 ) {
mystr.clear() ;
int l = strlen(ss) ;
rep( i , l ) {
if ( ss[i] == '<' ) mystr.movef() ;
else if ( ss[i] == '>' ) mystr.moveb() ;
else if ( ss[i] == '-' ) mystr.del() ;
else mystr.insert( ss[i] ) ;
}
printf("Case %d: %s\n" , ++ca , mystr.show().c_str() ) ;
}
}
Problem I: Longest Lane (By Xioumu)(VH)
Time Limit: 10 s
找一个多边形内部的最长的线段。可以是任意多边形。
Solution
Tag:计算几何
枚举任意两顶点,判断这两点形成的直线最长有多长在多边形里。
判断这个直线的长度有多长只需让多边形的边界来截这个直线,把这个直线截成很多段,每一段都不再与多边形的边有不严格的相交。
这样对于每一段,我们只需要判断这段的中点是否在多边形内即可判断这条线段是否在多边形内。最后在拼接起来,看最长的线段有多长。
注意这里的线段可以与边界重合。
/*
* Author: xioumu
* Created Time: 2013/4/24 14:36:47
* File Name: woj1479.cpp
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<string>
#include<map>
#include<set>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clr(x) memset(x,0,sizeof(x))
#define clrs( x , y ) memset(x,y,sizeof(x))
#define out(x) printf(#x" %d\n", x)
#define sqr(x) ((x) * (x))
typedef long long lint;
const int maxint = -1u>>1;
const double eps = 1e-8;
const double pi = acos(-1.0);
int sgn(const double &x) { return (x > eps) - (x < -eps); }
struct point {
double x, y;
point(double _x = 0, double _y = 0): x(_x), y(_y) {
}
void input() {
scanf("%lf%lf", &x, &y);
}
void output() {
printf("%.11f %.11f\n", x, y);
}
double len() const {
return sqrt(x * x + y * y);
}
};
bool operator==(const point& p1, const point& p2) {
return sgn(p1.x - p2.x) == 0 && sgn(p1.y - p2.y) == 0;
}
bool operator<(const point& p1, const point& p2) {
return sgn(p1.x - p2.x) == 0 ? sgn(p1.y - p2.y) < 0 : p1.x < p2.x;
}
point operator+(const point& p1, const point& p2) {
return point(p1.x + p2.x, p1.y + p2.y);
}
point operator-(const point& p1, const point& p2) {
return point(p1.x - p2.x, p1.y - p2.y);
}
double operator^(const point& p1, const point& p2) {
return p1.x * p2.x + p1.y * p2.y;
}
double operator*(const point& p1, const point& p2) {
return p1.x * p2.y - p1.y * p2.x;
}
point operator / (const point& p1, const double& x) {
return point(p1.x / x, p1.y / x);
}
bool intersect(point a,point b,point c,point d,point &e)
{
double d1 = (b-a) * (c-a), d2 = (b-a) * (d-a),
d3 = (d-c) * (a-c), d4 = (d-c) * (b-c);
if (sgn(d1)*sgn(d2) >= 0)
return false;
e = point( (c.x*d2 - d.x*d1) / (d2-d1) ,
(c.y*d2 - d.y*d1) / (d2-d1) );
return true;
}
double to_normal(double c) {
if (sgn(c - 1) >= 0) return 1.0 - eps;
if (sgn(c - (-1)) <= 0) return -1.0 + eps;
return c;
}
int get_position(point p, const vector<point>& pol, int n) {
double ang = 0;
for (int i = 0; i < n; ++i) {
point p1 = pol[i] - p, p2 = pol[i + 1] - p;
if (sgn(p1.len()) == 0 || sgn(p2.len()) == 0)
return 2;
double c = (p1 ^ p2) / (p1.len() * p2.len());
c = to_normal(c);
ang += sgn(p1 * p2) * acos(c);
}
ang = abs(ang);
return ang < 0.5 * pi ? -1 : (ang < 1.5 * pi ? 0 : 1);
}
vector<point> p;
int n;
void init() {
scanf("%d", &n);
p.clear();
rep (i, n) {
point tmp;
tmp.input();
p.push_back(tmp);
}
p.push_back(p[0]);
}
double get_distance(const point&p, const point& p1, const point& p2) {
return abs((p1 - p) * (p2 - p) / (p1 - p2).len());
}
void getMid(vector<point> &mid, point be, point en, point x, point y) {
int falg = 1;
if (sgn(get_distance(x, be, en)) == 0)
mid.push_back(x), falg = 0;
if (sgn(get_distance(y, be, en)) == 0)
mid.push_back(y), falg = 0;
point e;
if (falg && intersect(be, en, x, y, e)) {
mid.push_back(e);
}
}
double getMaxLen(point be, point en) {
if (en < be) swap(be, en);
vector<point> mid;
mid.push_back(be);
mid.push_back(en);
rep (i, sz(p) - 1) {
getMid(mid, be, en, p[i], p[i + 1]);
}
sort(mid.begin(), mid.end());
int stage = 0;
double sum = 0;
rep (i, sz(mid) - 1) {
if (mid[i] == be) stage = 1;
if (mid[i] == en) stage = 2;
point tmp = (mid[i] + mid[i + 1]) / 2;
if (get_position(tmp, p, sz(p) - 1) < 0) {
if (stage == 0) sum = 0;
else if (stage == 1) return -1e100;
else {
return sum;
}
}
else sum += (mid[i + 1] - mid[i]).len();
}
return sum;
}
void gao() {
double ans = -1e100;
rep (i, sz(p) - 1)
rep (j, i) {
double res = getMaxLen(p[i], p[j]);
ans = max(ans, res);
}
printf("%.4f\n", ans);
}
int main() {
//freopen("woj1479.out", "w", stdout);
int T, ca = 1;
scanf("%d", &T);
while (T--) {
init();
printf("Case %d: ", ca++);
//printf("%d\n", n);
gao();
}
return 0;
}
Problem J: Two Strings(E)
Time Limit: 3 s
两个字符串,有两种操作,一种是交换相邻两个字符(不需要代价),一种是把一个字符变成另外一个字符(代价为ascii码之差的绝对值),问一个字符串变成另外一个字符串的最小代价。
Solution
Tag:贪心
因为交换不需要代价,所以可以任意调整一个字符串里的字符顺序。
然后首先把相同的字符给匹配了,对于不相同的,每次匹配和其ascii相差1的就好,具体见代码。
/*
* Author: chlxyd
* Created Time: 2013/4/19 16:12:21
* File Name: test.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
int T , n ;
char s1[110000] , s2[110000] ;
int a[30] ;
int main(){
//freopen("S.in","r",stdin) ;
//freopen("s.out","w",stdout) ;
scanf("%d" , &T ) ;
int ca = 0 ;
while ( scanf("%d" , &n ) == 1 ) {
scanf("%s %s" , s1 , s2 ) ;
clr(a) ;
rep( j , n )
a[s1[j]-'a'+1] ++ ;
rep( j , n )
a[s2[j]-'a'+1] -- ;
int ans = 0 ;
repd( i , 26 , 1 ) {
ans += abs(a[i]) ;
a[i-1] += a[i] ;
}
printf("Case %d: %d\n" , ++ca , ans ) ;
}
}
UPD:代码在资源里提供了下载
UPD1:方便大家把代码贴出了
UPD2:I题解及代码已更新