珠排序Bead Sort
基本信息
珠排序是一种自然排序算法,由Joshua J. Arulanandham, Cristian S. Calude 和 Michael J. Dinneen 在2002年发展而来,并且在欧洲理论计算机协会(European Association for Theoretical Computer Science,简称EATCS)的新闻简报上发表了该算法。无论是电子还是实物上的实现,珠排序都能在O(n)时间内完成;然而,该算法在电子上的实现明显比实物要慢很多,并且只能用于对正整数序列进行排序。并且,即使在最好的情况,该算法也需要O(n2) 的空间。
算法概述
珠排序可以类比于珠子在平行的竖直杆上滑动,就像算盘一样,然而,每一竖直杆都有珠子数目的限制。因此,初始化就相当于在竖直的杆上悬挂珠子,在第一步中,排列就被显示为n=5行的珠子在m=4列队竖直杆上。每一行右边的数字意味着该行在问题中被表示的数;第1,2行表示正整数3(因为它们都有3个珠子)而顶层的一行表示正整数2(因为它只含有2个珠子)。如果我们要允许珠子掉落,那么每行表示已排序的整数。第1行表示在集合中最大的数,而第n行表示最小的数。如果按照前面提到的规则(行包含一系列在竖直杆1到k的珠子,并且让k+1到m竖直杆都空),那么它会出现这种情况。
允许珠子掉落的行为在物理意义上就是允许珠子从高的行掉落至低的行。如果被行a表示的值小于被行a+1表示的值,那么一些珠子就会从a+1掉落至a;因为行a不包含足够的珠子防止珠从a+1行掉落,所以这一定会发生。
用机械装置实现的珠排序类似于计数排序;每一杆上的数字与那些在所有数中等于或少于该数字的数量相当。
复杂度
珠排序可以是以下复杂度级别:
O(1):即所有珠子都同时移动,但这种算法只是概念上的,无法在计算机中实现。O(√n):在真实的物理世界中用引力实现,所需时间正比于珠子最大高度的平方根,而最大高度正比于n。
O(n):一次移动一列珠子,可以用模拟和数字的硬件实现。
O(S),S是所有输入数据的和:一次移动一个珠子,能在软件中实现。
先了解一个概念,不然不容易理解,一个数字3用3个1来表示。一个数字9用9个1来表示,珠排序中的珠指的是每一个1,它把每一个1想像成一个珠子,这些珠子被串在一起,想像下算盘和糖葫芦
上图1中的三个珠就表示数字3,两个珠表示数字2,这个OK了继续,这里的3和2都叫bead
图2(a)中有两个数字,4和3,分别串在四条线上,于是数字4的最后一个珠子下落,因为它下边是空的,自由下落后变成图2(b)
图2(c)中随机给了四个数字,分别是3,2,4,2,这些珠子自由下落,就变成了(d)中,落完就有序了,2,2,3,4
以上就是珠排序的精华
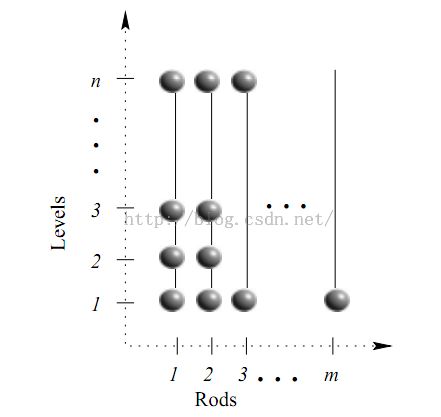
上图3中的n表示待排序数组的长度,有多少数字就有多少层,横向表示一层
m表示有多少个珠子,就是多少个1,这取决于最大数是几
比如待排数组[6 2 4 1 5 9]

让珠子全部做自由落体运动
9没有什么好落的,它在最底层
5也没有什么好落的,全部有支撑点
1同样不需要滑落
4除了第一个珠子不动外,其它三颗全部下落,落到1的位置变成下边这样
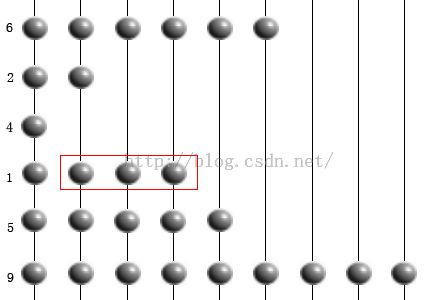
过程的细节不画了,原则就是你下边有支点,你就不用再滑落了,最后变成下边这样,排序完毕
从上到下顺序输出即可得到结果:[ 1 2 4 5 6 9]

