扫描探针显微术入门(6)
本文主要内容来源于V. L. Mironov 的“Fundamentals of scanning probe microscopy”。根据个人对SPM的理解略有改编。
隧道谱测量
利用STM可以测量样品上任一点的,探针样品隧道接触伏安特性(VAC)以此来研究样品表面局域电子密度等特性。偏置电压通常在0.1–1 V 之间,隧道电流在 0.1~1 nA之间。隧道接触电阻Rt在10^8 到 10^10 欧姆这个量级范围内。对于通常的材料,样品本身的电阻Rs 要远小于Rt,所以VAC 主要由样品上隧道接触点附近很小范围内的材料特性决定。
图 12 隧道接触的等效电路
隧道接触VAC 主要取决于样品的电子能级分布。图 13 给出了两种不同金属隧道接触时的电子能级示意图。
图 13 两种不同金属隧道接触时的电子能级示意图
隧道电流的形成主要由费米面附近的电子参与形成。在正向电压偏置时,电子从探针导带的填充态向样品导带的 free states 运动。当反向电压偏置时,电子从样品流向探针。隧道电流的大小由偏置电压、势垒传导系数和费米面的态密度决定,如果电子能级近似为连续分布时,隧道电流可以表达为如下式子:
在上面式子中 A 为常数D( E ) 为势垒的barrier transparency; ρP( E ) , ρS( E ) 为针尖和样品的态密度。f ( E )是费米分布函数。当势垒为理想的方形势垒,探针在费米面附件的态密度为常量时,电流表达式可以写为:
在这种情况下,隧道电流随电压的函数关系取决于样品的态密度。实际应用中,可以通过计算隧道电流对电压的导数来估算ρS( E )的值。

由于隧道电流对样品表面的态密度非常的敏感,隧道谱需要在高真空环境下测量的,另外由于电子的热激发会严重的影响采集到的隧道谱,因此测量需要在低温环境中进行。
金属—金属隧道结
在STM发明之前,就已经有大量的实验工作来研究两种金属之间的电子隧穿特性了。当电压很小时,隧道电流近似线性依赖于所加偏压。这时,隧道接触的电导率由势垒的形状决定。
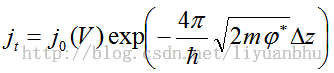
当电压很高时,势垒的形状会发生很大的改变,电流将遵循Fowler-Nordheim 公式给出的关系。 图 14 给出了一个金属-金属隧道接触VAC的典型曲线。
图 14 金属-金属隧道接触VAC的一个典型曲线
从上图中可以看出,金属-金属隧道接触VAC曲线是非线性、对称的。
金属-半导体隧道接触的VAC曲线
半导体材料通常具有更加复杂的电子能量谱结构。
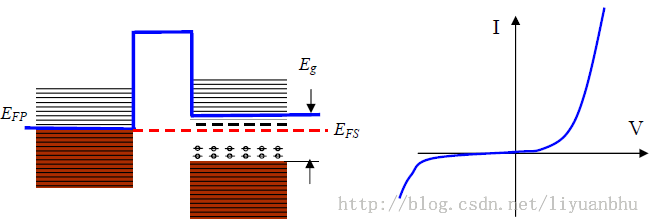
图 15 金属-半导体隧道接触的能级和典型的VAC曲线
半导体材料存在的带隙和impurity levels使得金属-半导体隧道接触VAC呈现出非常强的非线性。隧道电流的形成受到表面态密度还有表明吸附的其他原子对能级的影响。因此,测量半导体材料的局域隧道谱都是在高真空环境中完成的。无法控制的表面吸附的原子会导致实验得到的隧道谱很难给出清晰的物理解释。除此之外,热激发会使局域态形成的离散能级显著变宽,并且严重干扰导带和价带边缘的位置。 例如,图55给出了GaAs的隧道谱。

图. 55. GaAs晶体表明的STM隧道谱
隧道谱可以使我们获得导带和价带相对于费米面的位置,同时还能观察到半导体能隙由于态的impurity 而产生的峰值。
金属-超导体接触伏安特性
在超导体材料中,相变伴随着在超导临界温度以下时电子能级分布的重新排布。低温时,超导对中的电子聚集在导带之下的能级中,被能隙Δ所分割。金属-超导体接触的能级分布如图56所示。
图56 金属-超导体接触的电子能级
正偏压时,只有当eV>Δ时才有隧道电流。简单起见,我们忽略了薄势垒导致的电势下降,电子从针尖隧穿进入超导体样品的自由态。(Fig. 57 (a))
图57 金属-超导体接触的电子能级 (a)正偏压 (b) 反偏压
反偏压时,隧穿的图景有些复杂。隧穿过程中系统的能量是不变的,在这种情况下隧穿过程如下过程发生。超导对分裂,因此一个电子损失能量去到金属费米面附近的自由态。第二个电子,获得Δ的能量,跳入超导体能带的激发态。因此,在温度T=0K时金属-超导体接触的隧穿伏安特性在eV>Δ包含两个分支(图. 58 (a))。相应的超导体谱的态密度见图58b。
图. 58. 金属-超导体接触的伏安特性 (a)
在 T = 0 (蓝色线条)超导体的态密度 (b) .
(红线给出了伏安特性和 T ≠ 0 时的态密度)
在非0温度下,电子的态密度被部分的扰动,所以通过测量伏安特性获得的超导体的谱的特性不是很精确。扫描隧道谱的一个应用案例是研究各向同性样品的电子特性。在这种情况下,同时获得样品表面的形貌和伏安特性使我们可以观察到复合结构的不同相的分布情况,通过研究technological parameters和电子特性的相关性。实际上,在样品表明不同地方测量获得伏安特性使我们可以研究非均匀分布结构的样品的超导相的分布。为这个目的,在扫描获得样品形貌的同时在各点获得伏安特性曲线。利用局域伏安特性曲线,可以获得 Δ 参数,进而获得Δ = f (x,y)分布,表征了样品超导态的结构特征。
本人不懂固体物理,对STM隧道谱也没什么了解。这里是根据原文按照自己的理解翻译的,可能会有不少错误。建议大家还是去读原文,本文哪些地方写错了也请大家指正。

