POJ 1228(稳定凸包)
|
Language: Default
Grandpa's Estate
Description
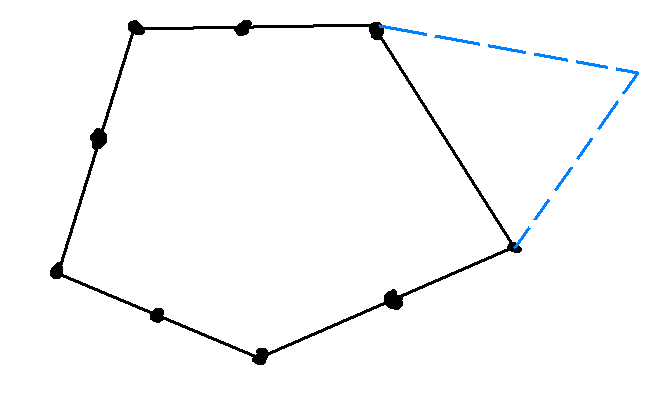
Kamran the Believer继承了祖母的一个凸多边形庄园. 庄园外围用绳子和木桩围起. 但一些绳子和木桩缺失了.帮忙看一下用剩余木桩围起的庄园是否是稳定凸包(即剩下的钉子能确定一个唯一的凸包).
Input
第一行一个数据组数 t (1 <= t <= 10).
对于每组数据,第一行为 n (1 <= n <= 1000) 表示木桩数. 接下来n行,每行为木桩坐标(
x,y),保证整数.
Output
对每组数据输出YES 或 NO ,表示其是否稳定.
Sample Input 1 6 0 0 1 2 3 4 2 0 2 4 5 0 Sample Output NO Source
Tehran 2002 Preliminary
|
要想让一个凸包稳定,当且仅当凸包上任意一条边有3个以上的木桩(包括端点)
证明:
只要在建完凸包后,枚举,边上的第3点即可。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<cctype>
#include<iostream>
#include<functional>
#include<algorithm>
using namespace std;
#define MAXT (10+10)
#define MAXN (1000+10)
//#define sqr( x ) (x*x)
int sqr(int x){return x*x;}
struct P
{
int x,y;
P(){}
P(int _x,int _y):x(_x),y(_y){}
friend istream& operator>>(istream &cin,P &a)
{
cin>>a.x>>a.y;return cin;
}
friend double dis(P a,P b)
{
return sqrt(double(sqr(a.x-b.x)+sqr(a.y-b.y)));
}
}a[MAXN];
struct V
{
int x,y;
V(){}
V(int _x,int _y):x(_x),y(_y){}
V(P a,P b):x(b.x-a.x),y(b.y-a.y){}
friend int operator*(V a,V b)
{
return a.x*b.y-a.y*b.x;
}
};
int cmp(P A,P B)
{
int temp=V(a[1],A)*V(a[1],B);
if (temp>0) return 1;
else if (temp==0&&dis(a[1],A)<dis(a[1],B)) return 1;
else return 0;
}
int t,n,st[MAXN];
bool solve()
{
int size=1;st[0]=1;
st[1]=1;
int j=2;
while (j<=n)
{
if (size<2||V(a[st[size-1]],a[st[size]])*V(a[st[size]],a[j])>0)
{
st[++size]=j++;
}
else size--;
}
a[++n]=a[1];
st[++size]=n;
for (int i=1;i<size;i++)
{
/*
int k=st[i-1]+1;
for (;k<st[i+1];k++)
if (k!=st[i]&&V(a[st[i]],a[st[i+1]])*V(a[st[i]],a[st[k]])==0) break;
if (k==st[i+1]) return 0;
*/
int k=1;
for (;k<n;k++)
if (k!=st[i]&&k!=st[i+1]&&V(a[st[i]],a[st[i+1]])*V(a[st[i]],a[k])==0) break;
if (k==n) return 0;
}
return size>=4;
}
int main()
{
// freopen("poj1228.in","r",stdin);
cin>>t;
while (t--)
{
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
if (n<6)
{
cout<<"NO\n";
continue;
}
int p=1;
for (int i=2;i<=n;i++) if (a[i].x<a[p].x||(a[i].x==a[p].x)&&(a[i].y<a[p].y)) p=i;
swap(a[1],a[p]);
sort(a+2,a+1+n,cmp);
// cout<<dis(P(0,0),P(1,0))<<dis(P(0,0),P(1,0));
if (solve()) cout<<"YES\n";
else cout<<"NO\n";
}
return 0;
}
备注:不知为何,将sqr替换成define 结果会输出"nan"…… 彩 蛋 ?