算法学习笔记 二叉树和图遍历—深搜 DFS 与广搜 BFS
图的深搜与广搜
马上又要秋招了,赶紧复习下基础知识。这里复习下二叉树、图的深搜与广搜。从图的遍历说起,图的遍历方法有两种:深度优先遍历(Depth First Search), 广度优先遍历(Breadth First Search),其经典应用走迷宫、N皇后、二叉树遍历等。遍历即按某种顺序访问“图”中所有的节点,顺序分为:
- 深度优先(优先往深处走),用的数据结构是栈, 主要是递归实现;
- 广度优先(优先走最近的),用的数据结构是队列,主要是迭代实现;
对于深搜,由于递归往往可以方便的利用系统栈,不需要自己维护栈,所以通常实现比较简单。而对于广搜,则需要自己维护一个队列,且由于队列大小未知,底层存储的物理结构采用链式存储。
【文章地址为:http://blog.csdn.net/thisinnocence】
二叉树概念和性质
二叉树是每个节点最多有两个子树的树结构,常被用于实现二叉查找树和二叉堆。在图论中,二叉树定义是一个连通的无环图,并且每一个顶点的度不大于2。二叉树和树有很多相似之处,但并不是树的特殊情形,主要有以下三点主要差别:
- 树中结点的最大度数没有限制,而二叉树结点的最大度数为2;
- 树的结点无左、右之分,而二叉树的结点有左、右之分;
- 树的结点个数至少为1,而二叉树的结点个数可以为0
- 结点的度:结点所拥有的子树的个数称为该结点的度。二叉树就只有 0,1,2 三种情况;
- 叶结点:度为 0 的结点称为叶结点,或者称为终端结点;
- 分枝结点:度不为 0 的结点称为分支结点,一棵树的结点除叶结点外,其余的都是分支结点;
- 结点的层数: 规定树的根结点的层数为 1,其余结点的层数等于它的双亲结点的层数加 1;
- 树的深度: 树中所有结点的最大层数称为树的深度;
- 路径、路径长度。如果一棵树的一串结点 n(1), n(2), …, n(k) 有如下关系:结点 n(i) 是 n(i+1) 的父结点 (1≤i<k), 就把 n(1),n(2),…,n(k) 称为一条由 n(1) 至 n(k) 的路径。这条路径的长度是 k-1;
- 满二叉树: 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在同一层上;
- 完全二叉树: 深度为 K 的,有 N 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中按层序编号从 1 至 N 的结点一一对应;
- 堆是一种完全二叉树,常用的排序算法、Dijkstra 算法、Prim 算法等都常用堆优化;
- AVL树:它是最先发明的自平衡二叉查找树, 名字来源于其发明者,AVL 树中任何节点的两个子树的高度最大差别为 1, 查找、插入和删除在平均和最坏情况下都是 O(logn);
- 性质1:在二叉树的第 i 层上至多有 2i-1 个结点 (i≥1);
- 性质2:深度为 k 的二叉树上至多含 2k-1 个结点 (k≥1);
- 性质3:对任何一棵二叉树,若它含有 n0 个叶子结点、n2 个度为 2 的结点,则:n0 = n2+1;
- 性质4:具有 n 个结点的完全二叉树的深度为 log2n+1;
- 性质5:若对含 n 个结点的完全二叉树从上到下且从左至右(即按层序)进行 1 至 n 的编号,则对完全二叉树中任意一个编号为 i 的结点:
(1) 若 i=1,则该结点是二叉树的根,无双亲,否则,编号为i/2 的结点为其双亲结点;
(2) 若 2i>n,则该结点无左孩子,否则,编号为 2i 的结点为其左孩子结点;
(3) 若 2i+1>n,则该结点无右孩子结点,否则,编号为2i+1 的结点为其右孩子结点;
小实验(C 实现)
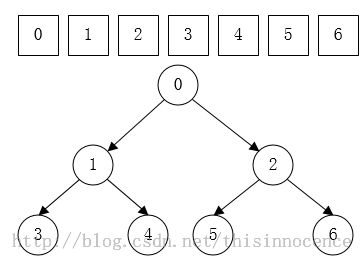
这里首先用一个数组生成一个完全二叉树(链式存储), 然后深搜用前序遍历,广搜借助自己实现的一个队列(链式存储)来进行,图如下所示:
代码为:
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int data;
struct Node * left;
struct Node * right;
} BitNode, *BiTree;
typedef BiTree QElemType; // 定义队列元素类型
typedef struct QNode {
QElemType data; // 存放树节点指针
struct QNode *next;
} QNode, *QueuePtr; // 队列节点和节点指针
typedef struct LinkQueue {
QueuePtr front, rear;
} LinkQueue; // 队列前后指针: 队首,队尾
/* 初始化队列 */
int InitQueue(LinkQueue *Q) {
QueuePtr s = (QueuePtr) malloc(sizeof(QNode));
if (!s) return 0;
Q->front = s;
Q->rear = s;
return 1;
}
/* 入队 */
int EnQueue(LinkQueue *Q, QElemType e) {
if (e == NULL) return 0;
QueuePtr s = (QueuePtr) malloc(sizeof(QNode));
if (!s) return 0;
s->data = e;
s->next = NULL;
Q->rear->next = s;
Q->rear = s;
return 1;
}
/* 出队 */
int DeQueue(LinkQueue *Q, QElemType *e) {
if (Q->front == Q->rear) {
return 0;
} // 首位指针相等,队列空,出队失败
QueuePtr p;
p = Q->front->next; // 头结点不放数据,其后继结点作为队首,出队
*e = p->data;
Q->front->next = p->next; // 队首指针后移一个节点
if (Q->rear == p) {
Q->rear = Q->front;
} // 尾指针如果指向的是头结点后第一个节点,则令其指向队首指针。 即队列只有一个数据节点的情况
free(p);
return 1;
}
/* 利用数组 a 创建二叉树,递归的编写技巧在于设计好函数接口 */
void CreateTree(BiTree *bt, int a[], int len, int index) {
if (index > len - 1)
return;
(*bt) = (BiTree) malloc(sizeof(BitNode)); // 指针变量初始化堆区的内存,c 用 malloc 函数
(*bt)->data = a[index];
(*bt)->left = NULL; // 不能能省略,当其为叶节点时,指针域为 NULL,而且常作为程序判断条件
(*bt)->right = NULL;
CreateTree(&((*bt)->left), a, len, 2 * index + 1);
CreateTree(&((*bt)->right), a, len, 2 * index + 2);
}
/* 前序遍历二叉树 , 属于深度优先遍历 DFS */
void PreOrderTraverse(BiTree bt) {
if (bt == NULL)
return;
printf("%d ", bt->data); // 操作节点数据
PreOrderTraverse(bt->left);
PreOrderTraverse(bt->right);
}
/* 按层遍历,即广度优先遍历 BFS */
void BFSTraverse(BiTree bt) {
LinkQueue *Q = (LinkQueue *) malloc(sizeof(LinkQueue));
BiTree e;
InitQueue(Q);
EnQueue(Q, bt);
while (Q->front != Q->rear) {
DeQueue(Q, &e);
printf("%d ", e->data);
EnQueue(Q, e->left);
EnQueue(Q, e->right);
}
}
int main() {
int arr[] = { 0, 1, 2, 3, 4, 5, 6};
BiTree root;
CreateTree(&root, arr, sizeof(arr) / sizeof(int), 0);
printf("PreOrderTraverse: ");
PreOrderTraverse(root);
printf("\nBFSOrderTravesre: ");
BFSTraverse(root);
return 0;
}
/*
程序运行如下:
PreOrderTraverse: 0 1 3 4 2 5 6
BFSOrderTravesre: 0 1 2 3 4 5 6
*/