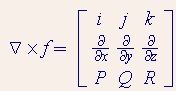散度(Divergence)和旋度(Curl)

 散度(Divergence)

散度的讨论应从向量和向量场说起。向量是数学中研究多维计算的基本概念。比如，速度可以分解为相互独立的分量，则速度就是一个多维的向量。假如空间中的每一个位置都有一个向量属性的话，这个空间就叫做向量场。比如，游泳池里的水的速度就是一个向量场。

散度就是作用在向量场上的算子。它把向量场映射到标量场。其中某点的标量代表该点的向量是“流入”的，还是“流出”的。

比如在游泳池中考虑一个封闭的正方体区域，在该区域的六个表面中，要么有液体流出，要么有液体流入。设流出为正，流入为负，把六个面的流量相加，如果为正，则代表该区域有正的散度。反之则是负的散度。这就是散度界定中“通量”的概念。

现在如果取一个任意的封闭曲面，则它的通量为曲面表面的向量场在曲面法向量上的分量的积分。假如该封闭曲面的体积无限小，则极限是曲面内某一点，这个极限通量就是散度。从这个角度说，上文的“流入”（散度小于零）表示了通量的湮灭，而“流出”（散度大于零）表示了该区域有新的通量产生。

就如之前的流体文中提到的，由于水流不会凭空产生或消失，即不可压缩流体的总散度必为零。在流体力学中，散度指流体运动时单位体积的改变率。

散度的数学表示法

在笛卡尔坐标系Oxyz中，若向量场为(P(x,y,z), Q(x,y,z), R(x,y,z))
则对以上三个分量分别对x, y, z求偏导数，然后把三个结果相加。

一般来说，使用div或者向下的三角形加一点来表示散度。

假如某处散度为零，则称该处divergence free。

散度的概念来源于物理学中的静电学。十九世纪末，英国物理学家海维赛德（Heaviside）提出既然静电场中的电荷是电场力的原因，那么吧电荷看作一个体积微小的一点，那么该点的电场力“聚集度”就等于这个微小体积散发出的所有电场力的总和。他又把这种“聚集度”称为“散度”。并且他给出了散度计算的公式。从以上可以看出，散度所考虑的对象是某一个点及其接近的很小的空间。

但是，光用散度无法完全描述电场的属性。1873年，英国物理学家麦克斯韦在一篇论文中使用了哈密顿的四元素方法。

旋度(Curl)

还记得以前提到过的四元素吗?
http://blog.csdn.net/wangxiaojun911/article/details/4644243

对四元素q = i * A + j * B + k * C + D求偏导数。定义微分算子(d/dx)i + (d/dy)j + (d/dz)k, 则对原四元素其中前三项的微分很特别。它的微分结果分为两部分，第一部分是A, B, C分别对x, y, z的偏导，若把(A,B,C)看作向量，其结果正是负的散度。（注意i*i=-1, j*j=-1, k*k=-1）

第二部分则是被称为“旋度”的部分。为(dC/dy-dB/dz)i+(dA/dz-dC/dx)j+(dB/dx-dA/dy)k。麦克斯韦之所以使用了旋度这个名字，是他认为这个量表示了向量场转动倾向的属性。

与散度在一个小位元上是标量不同，旋度运算的结果仍然是一个向量，表示了某个局部微元上的旋转倾向。举例来说，把北极圈看作一个极小的局部对象讨论，一个沿着纬度方向的向量场会造成旋度而散度为零；沿着经度方向的向量场会造成散度而旋度为零。

旋度的数学表示法

假如坐标系和向量场如最开始定义（P，Q，R），令p()为求偏导数，散度的定义为：
(p(R)/p(y)-p(Q)/p(z),
 p(P)/p(z)-p(R)/p(x)
 p(Q)/p(x)-p(P)/p(y))

参考文献：
zh.wikipedia.org