模式识别技术漫谈(5)
神经网络基本原理
学习模式识别我个人觉得从神经网络入手可能是个较好的选择,一方面可以避免一下子就陷入复杂的公式推导中,另一方面可以让我们较快就能体验到模式识别是个什么样的技术,因为我们可以利用matlat或openCV非常方便地进行实践(学习一种技术,多去实践非常有助于对理论知识的理解)。神经网络技术是从仿生的角度来思考模式识别技术,探寻模仿人类的智能一直以来是科学界所研究的目标,神经网络技术就是基于此而产生的,但是神经网络能够得到应用还是因为数学问题方面得到了解决,最优化理论中的梯度下降法便是神经网络实现原理的核心,梯度下降算法是一个循环的计算过程:
1. 为算法模型参数值选择初始值,或随机选择些初始值;
2. 计算每个参数对应的损失函数的变化梯度;
3. 根据梯度值改变参数值,使得错误值变得更小;
4. 重复第二和第三步骤直至梯度值接近于0。
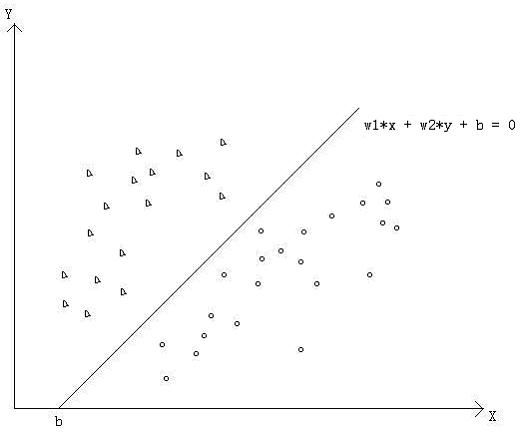
神经网络方法就是通过训练样本进行学习来拟合出一条分割线(对于维数是三维的识别,则是个平面或曲面,三维以上则是超平面或超曲面),如果这条分割线是一条直线(或平面,或超平面),则称为线性神经网络,否则为非线性神经网络,线性神经网络较好理解,理解了线性神经网络,对于非线性神经网络则能够更易理解,所以这里先以线性神经网络为例来解释神经网络的原理,下图是一个二维特征分布图,中间的一条直线是分割线,我们现在要关心的问题是这条分割线是如何计算出来,如果学过数学,我们知道可以用最小二乘法把它计算出来,但这里我们将要用神经网络的学习方法来把它学习出来:
从上图我们可以知道,只要我们能够得到w1,w2,b的值,则这条直线我们就可以求出来了,据此我们构造出如下所示的神经网络拓扑图:
从上图中的w1,w2,我们把它们称为权值,b称为阈值,神经网络的学习过程便是不断地调整权值和阈值,直至最后达到最小的错误率,对于线性神经网络,我们可以采用LMS算法,即最小均方差算法来求出权值和阈值,如下是LMS算法的描述:
原理:通过调整线性神经网络的权值(w)和阈值(b),使得均方差最小。
已知有样本集:{p1,t1},{p2,t2},{p3,t3}……{pn,tn}.(如果样本特征值是多维的,则p是个向量表达式)
求出均方差:mse = sum( e( i )2 ) / n = sum(t(i) – a(i))2 / n, 其中i = 1~n,a(i) = pi * w + b
假设第k步已分别求出权值梯度(Gw)和阈值梯度(G b),则第k+1步权值和阈值分别为:
w(k+1) = w(k) – Gw * α ;
b(k+1) = b(k) – G b *α ; α为学习率
下一步就是要怎么算出梯度,如果权值和阈值的变化能够使得均方差趋向最小,则便可以达到我们的目标,依此我们可以对均方差公式求对权值和阈值的偏导,这个偏导值便是我们所要的梯度值,它反应了权值或阈值变化与均方差的关系,偏导公式的演变(推导)如下:
əe2(i)/əw = 2e(i) * əe(i)/əw = 2e(i) * ə(t(i) – a(i))/əw = 2e(i) * ə[t(i) – (w*p + b)]/əw
= –2e(i) * p;
əe2(i)/əb = 2e(i) * əe(i)/əb = 2e(i) * ə(t(i) – a(i))/əb = 2e(i) * ə[t(i) – (w*p + b)]/əb
= – 2e(i);
第k步的平均差值表示为:e(k) = sum(e(i))/n;
于是最后我们就可以得到权值和阈值的变化方程式:
w(k+1) = w(k) – Gw * α = w(k) + 2 * e(k) * p * α;
b(k+1) = b(k) – G b * α = b(k) + 2 * e(k) * α;
其实,上面所描述的神经网络是一种单层的神经网络,早在1969年,M.Minsky和S.Papert所著的《感知机》书中对单层神经网络进行了深入分析,并且从数学上证明了这种网络功能有限,甚至不能解决象"异或"这样的简单逻辑运算问题。同时,他们还发现有许多模式是不能用单层网络训练的,真正让神经网络得到广泛应用的是1985年发展了BP网络学习算法,实现了Minsky的多层网络设想,BP网络是一种多层前馈型神经网络,其神经元的传递函数是S型函数(非线性函数),它可以实现从输入到输出的任意非线性映射,由于权值的调整采用反向传播(Back Propagation)学习算法,因此被称为BP网络,目前,在人工神经网络应用中,大部分是采用BP网络及其变化形式,它也是前向网络的核心部分,体现了人工神经网络的精华。BP神经网络不仅可用于模式识别,还可用于函数逼近、数据压缩应用中。
BP算法跟上面介绍的算法非常相似,也是根据均方差求权值和阈值的调整方向,也是通过对权值变量和阈值变量分别求偏导得到权值和阈值的修正梯度方向,差别在于BP神经网络有好几层,要从输出层开始,一层一层地计算出每层的权值变化和阈值变化(所以称为反向传播学习算法),另一个差别是有些网络层的神经元的传递函数采用log-sigmoid型非线性函数,对于这类函数需要对其进行求导。
BP算法的主要缺点是:收敛速度慢、存在多个局部极值、难以确定稳层个数和稳层节点的个数。所以在实际应用中,BP算法很难胜任,需要进行改进,主要有两种途径进行改进:一种是启发式学习算法(对表现函数梯度加以分析以改进算法),另一种是更有效的优化算法(基于数值最优化理论的训练算法)。启发式学习算法有这些:有动量的梯度下降法、有自适应lr的梯度下降法、有动量和自适应的梯度下降法、能复位的BP训练法等,基于最优化理论的算法有这些:共轭梯度法、高斯-牛顿法、Levenberg-Marquardt方法,这些改进的算法在matlab中都可以找得到,matlab提供了丰富的神经网络算法,除了BP神经网络,还有基于径向基函数的神经网络(如广义回归神经网络、概率神经网络)、反馈型神经网络(如Hopfield网络、Elman神经网络)、竞争型神经网络(如自组织特征映射神经网络、学习向量量化神经网络),所以学习神经网络,matlab是个非常好的工具,如果想看具体的实现方法,openCV提供了BP算法的实现,可惜目前openCV只实现BP算法,很希望有更多的神经网络算法能够在openCV中被实现。
对于神经网络,万不可过于迷信它的厉害,对于样本种类多、神经网络节点多,神经网络的收敛速度会很慢,导致学习要花费很长时间,由于存在多个局部极值点,导致初值不同和学习样本不同时,学习效果也不同,所以经常要多次学习才能够得到较好的效果,根据问题的复杂度,设计合适的神经网络的网络拓扑结构也是一个非常难的问题。神经网络是人类模仿生物神经网络原理的一个成果,但是还远远无法达到生物的神经网络功能,现在的人工智能技术甚至连蟑螂都不如,也比不上小小的蚂蚁,人工智能技术的研究还有非常漫长的路要走。