小谈并查集及其算法实现
并查集
一、算法介绍:
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。
并查集的基本操作有两个:
1:合并
union(x, y):把元素 x 和元素 y 所在的集合合并,要求 x 和 y 所在的集合不相交,如果两个集合相交则不合并。
2:查询
find(x):找到元素 x 所在的集合的代表,该操作常用于判断两个元素是否位于同一个集合,只要将它们各自的代表比较一下就可以了。
并查集类似一个森林,是用树形结构来实现的,所以以下的讲解用树形结构来构造模型:
事先声明:
(1)一个集合对应一棵树。
(2)一个集合中的元素对应一个节点。
二、算法实现:
一、初始化:
我们用n个节点表示n个元素,有一点要特别注意:一个节点,若它的父节点等于它本身,则说明这个节点是根节点。
定义数组 per[], per[x]代表x的父节点。初始化时我们把per[x] = x,相当于每个节点都是独立的根节点(每个根节点都代表一个集合)
//n 代表一共有n个元素(n个节点)
for(int i = 1; i <= n; ++i){
per[i] = i;
}
二、查找:
find(x),查找元素x所在的集合,即查找节点x在哪一棵树上,这里我们知道,在一棵树中,根节点是唯一的,父节点子节点都是相对而言的。要想确定节点x在哪一课树,我们只需要找到x的根节点就可以了。
如果判断节点x 和 节点y在不在同一棵树上,我们只需要找到x 和 y的根节点,若x和y的根节点相同,则x,y在同一颗树上,否则在不用的树上。
代码:
int find(int x){
int r = x;
//父节点等于自身的节点才是根节点,
//若 r 节点的父节点不是根节点,一直向上找。
if(r != per[x])
r = per[x];
return r;
}
图1.1
如图1.1所示:
我们令节点1为根节点。查找节点4在哪一棵树,我们只要找到4的根节点就可以了。
查找过程: 找到4的父节点per[4]为2,不等于它本身,继续向上查找, 2它的父节点per[2]为1,不等于它本身,继续向上查找,1的父节点per[1]为1等于它本身,说明1是根节点。
这里有一个路径压缩的优化, 当我们查找到4的根节点为1时,我们直接将per[4] = 1,即直接把4连在根节点1上,而且在查找4时还会找到2,可能还有其他的节点,将这些节点的per[]通通都设置为1,这样下次再查找4的子节点所在的树时,查找次数就缩短了1.
这里压缩路径有两种写法,一种是递归的,一种是非递归的。
1> 递归:
int find(int x){
if(x == per[x])
return x;
return per[x] = find(per[x]);
}
2>非递归
int find(int x){
int r = x;
if(r != per[x])
r = per[x];
int i = x, j;
while(i != r){
j = per[i];
per[i] = r;
i = j;
}
return r;
}
请读者自己模拟一下这两种压缩路径的方式有何不同。
三、合并:
合并x 和 y所在的树, 只需要把其中一个树的根节点设置为令一个树根节点的子节点即可;
void union(int x, int y){
int fx = find(x);//x的根节点为fx
int fy = find(y);//y的根节点为fy
if(fx != fy)
per[fx] = fy;
}
但是这里有一个问题, 是把 x的根节点设置为 y根节点的子节点,还是把y的根节点设置为x根节点的子节点。
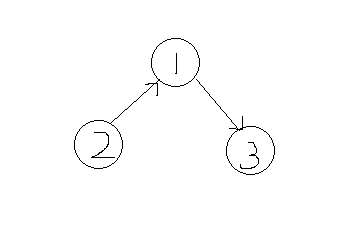
节点1和节点2是一棵树,根节点为1, 节点3是一棵树,根节点是自身为3.
图1.2
图1.3
如图1.2所示:
现在我们根节点3作为根节点1的子节点,此时查找2的根节点,只需要查找一次。
如图1,3所示
现在我们根节点1作为根节点3的子节点,此时查找2的根节点,需要先找到1,再找到3,多了一次查找。
所以这里存在一种优化。我们可以设置一个数组rank[ ],用它来记录每一棵树的深度,合并时如果两棵树的深度不用,那么从深度(rank)小的向深度(rank)达的连边。(但注意,压缩路径时会使树的深度发生变化,但我们不修改rank 的值)
int per[maxn];//记录父节点
int rank[maxn];//记录树的深度
void init(){//初始化n个节点
for(int i = 1; i <= n; ++i){
per[i] = i;
rank[i] = 0;
}
}
//找到根节点,压缩路径
int find(int x){
if(x == per[x])
return x;
return per[x] = find(per[x]);
}
void union (int a, int b){
int fa = find(a);
int fb = find(b);
if(fb != fa){
if(rank[fa] < rank[fb]){
per[fa] = fb;
}
else{
per[fb] = fa;
if(rank[fa] == rank[fb]) rank[fa]++;
}
}
}
三、基础例题解析:
例题一:HDOJ1232--畅通工程【基础并查集】
题目大意:给出n个城市, m条无向路,问最少再修几条路使所有城镇都连通。
最基础的并查集问题,递归压缩路径,没有深度优化
AC代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#define maxn 1100
#define INF 0x3f3f3f3f
using namespace std;
int per[1100];
int n, m;
//初始化节点
void init(){
for(int i = 1; i <= n; ++i)
per[i] = i;
}
//查找根节点,递归压缩路径
int find (int x){
if(x == per[x])
return x;
return per[x] = find(per[x]);
}
//合并根节点
void join(int x, int y){
int fx = find(x);
int fy = find(y);
if(fx != fy)
per[fx] = fy;
}
int main (){
while(scanf("%d", &n),n){
scanf("%d", &m);
init();
int a, b;
while(m--){
scanf("%d%d", &a, &b);
join(a,b);
}
int ans = 0;
//判断图中有几棵树,只需要判断有几个根节点即可
//判断方法;父节点等于本身的节点就是根节点
for(int i = 1; i <= n; ++i){
if(per[i] == i)
ans++;
}
//把这些根节点连通,最小需要ans - 1条边
printf("%d\n", ans - 1);
}
return 0;
}
例题二:HDOJ 1272--小希的迷宫【并查集 && 判环 && 判断树的个数】
考察点:判断是否成环,判断图中树的个数
AC代码:非递归压缩路径,有深度优化
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define maxn 100000 + 100
int per[maxn];
int vis[maxn];
int flag;
int ran[maxn];
//查找根节点,非递归压缩路径
int find(int x) {
int r = x;
while(r != per[r])
r = per[r];
int i,j;
i = x;
while(i != r){
j = per[i];
per[i] = r;
i = j;
}
return r;
}
//合并根节点,深度优化
void jion (int a, int b){
int fa = find(a);
int fb = find(b);
if(fb != fa){
if(ran[fa] < ran[fb]){
per[fa] = fb;
}
else{
per[fb] = fa;
if(ran[fa] == ran[fb]) ran[fa]++;
}
}
else
flag = 0;//判断是否成环
}
int main (){
int a, b;
while(scanf("%d%d", &a, &b) != EOF){
if(a == -1 && b == -1)
break;
if(a == 0 && b == 0){
printf("Yes\n");
continue;
}
for(int i = 1; i <= 100000; ++i){
per[i] = i;
vis[i] = 0;
ran[i] = 0;
}
vis[a] = 1, vis[b] = 1;
flag = 1;
jion(a, b);
while(scanf("%d%d", &a, &b), a || b){
vis[a] = 1;//并不是所有的房间都用到了,所以需要标记一下
vis[b] = 1;
jion(a, b);
}
int ans = 0;
for(int i = 1; i <= 100000; ++i){
if(per[i] == i && vis[i])
ans++;
if(ans > 1){
flag = 0;
break;
}
}
if(flag) printf("Yes\n");
else printf("No\n");
}
return 0;
}
四、例题推荐:
HDU 4496--D-City 【并查集 && 删边】
解析:HDU 4496
HDU 1598--find the most comfortable road【并查集 + 枚举】
解析:HDU 1598
HDU 2473--Junk-Mail Filter 【并查集 && 删点】
解析:HDU 2473
HDU 3635--Dragon Balls【并查集】
解析:HDU 3635
本人菜鸟一个,如有不对的地方希望各位大神纠正。有关带权并查集的问题会在日后更新