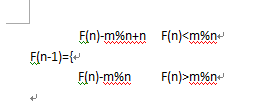算法与数据结构面试题(22)-求出在这个圆圈中剩下的最后一个数字
题目
n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,每次从这个圆圈中删除第m个数字 (第一个为当前数字本身,第二个为当前数字的下一个数字)。当一个数字删除后, 从被删除数字的下一个继续删除第m个数字。求出在这个圆圈中剩下的最后一个数字。
参考文章
http://blog.csdn.net/lzj509649444/article/details/7056742
个人理解
第一种思路
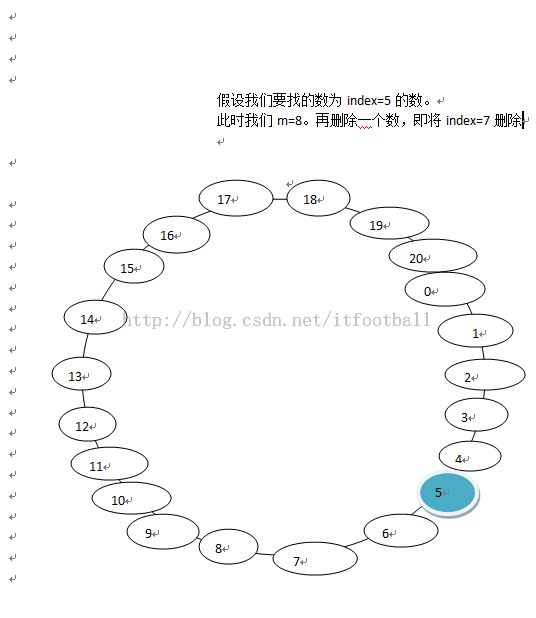
1.m=8删除过程
2.m=4的删除过程
分析
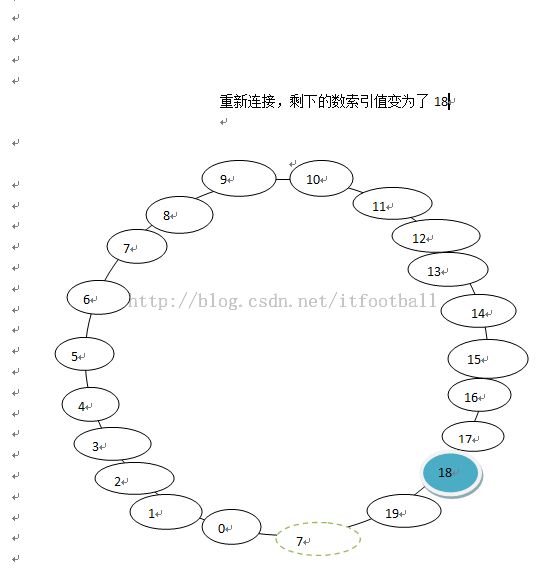
经过K次删除,我们要找的数在index=5处,但是经过K+1次删除后我们要找的数变成了index=18了。这index的变化和m以及目前剩余的数n有什么关系?
删除第m个数字,有3种情况:
求删除的数索引值
1.m>n,遍历超过一圈,这个时候删除的元素为第m%n个
2.m<n,遍历不超过一圈,这个时候删除的元素为第m个
3.m=n,删除的元素为第0个。
综上所述删除的数的索引可以用m%n来表示。
求第f(n)次和f(n-1)次的关系
第K次删除,设要找的数索引值为i。为f(n)
第K+1次删除,要找的数索引值为j。为f(n-1)
也要分2种情况:
1.删除的数索引值大于i。即m%n>i
j = n-m%n+i 18 = 21-8%21+5
2.删除的数索引值小于i。即m%n<i
j = i-m%n 1=5-4%21
因为i肯定是小于n的。所以i = i%n
总结
但是上面的公式含有两种情况,我们现在已知的条件是F(0)的位置,而无法得到F(n)的值,所以上面的公式推导失败。
第二种思路
因为我们要求的最后一个数的数值,那么我们求剩下的数在原始集合中的索引值index,就可以通过index-1得到该数。
所以公式要倒过来,变成了当F(0) = 0。求F(n)的问题,因此我们要将上面的图从后往前看,如何根据后一张图的位置推导出前一张图的位置。
假如m=8
进行K次删除以后:
此时n=20,剩下的数在当前位置的索引值为18,
那么在K-1次删除后:
n=21,剩下的数在什么位置。上图中很明显可以知道数在5的位置。能否找到一个递推公式呢?具体推理过程。上面的参考文章有推理过程,我们要做的是验证是否正确。
如果f(20,8)为18,m=8,n=21,那么
f(21,8) = (18+8)%21 = 5。
如果f(20,4) = 1,m=4,n=21,那么
f(21,4) = (1+4)%21 = 5。
其他多余的验证就不做了。
代码
public int getLastIndexByOnline(int n, int m) {
//n=0,空集.m=0,不删除
if (n < 1 || m < 1) {
return -1;
}
int last = 0;
//当n=1的时候,返回的就是下标就是0,当n>=2的时候才有必要做循环遍历
for (int i = 2; i <= n; i++) {
last = (last + m) % i;
}
return last;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int n = 20;
int m = 8;
Problem18 problem = new Problem18();
int index = problem.getLastIndexByOnline(n, m);
System.out.println("最后一个数是 : " + index);
}
输出
最后一个数是 : 0
总结
这题不在于考察你的代码能力,也不考察你的数据结构和算法。考察的是你的推导能力。