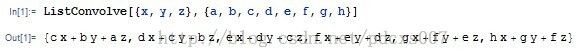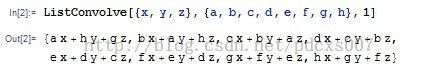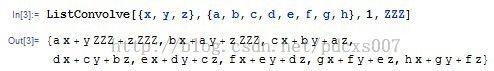Mathematica的卷积运算
相比Matlab,在平时理解概念时我更喜欢用Mathematica,因为,无疑的,Mathematica的强大的符号运算总会让人身心舒畅。最近信号与系统学习卷积。我在Mathematica中研究了相关的函数,自觉收获很大。故在此总结。
首先是离散信号的卷积。先介绍有限信号的卷积(这是上课时刚开始的例子,但是在Mathematica中却似乎是最难理解的函数了)。相关的函数是:
一、ListConvolve
帮助如下:
1、基本用法:ListConvolve[ker, list] 构造核ker和list的卷积。
出现的新概念是核。核即指核心,便是值输入的信号。list自然是单位冲击信号对应的响应了。以下是我的实验结果:
可见,其参数其实是一个单行的矩阵。默认情况下是,开始的一个结果ker的最后一个元素和list的第一个元素对其,而最后一个是ker的第一个元素和list的最后一个元素对其。于是,得到的结果个数和list的个数相同。
2、第三个参数:ListConvolve[ker, list, k] 形成循环卷积,其中 ker 中的 k个元素和 list 中的每个元素对齐。
再次出现新概念:循环卷积。意思是,当结果范围超出list时(这种情况是在刚刚的默认情况时没有出现的),循环相乘。实验结果如下:
可以见得,ker中的第一个元素:x,和a对其,然而y和z则对应于循环以后的h和g了。这就是循环卷积的意思了。
3、ListConvolve[ker,list,k,p] 当遇到循环时,不用循环元素,而是用p来代替。实验结果如下:
4、ListConvolve[ker,list,{kL,kR}] 形成循环卷积,它的第一个元素包含 list[[1]]ker[[kL]],最后一个元素包含 list[[-1]]ker[[kR]].
这里再次涉及到一些东西。最主要的是,list去内容的运算。本质上,list和ker其实都是一个列矩阵。实验如下:
因此,[[x]]表示取x行。例如:
因此,上述帮助的意思是,我们可以规定其开始和结束的地方。开始的地方是list[[1]]和ker[[kL]],结束的地方是list[[-1]]ker[[kR]],其中-1指最后一行。只是很有用的。
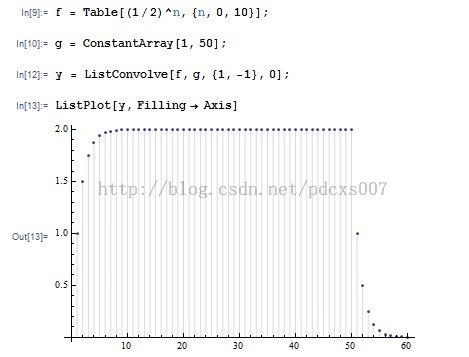
通过以上四种用法相结合,我们就可以得到我们想要的卷积运算。使用Table可以生成希望的矩阵,然后循环是用0来代替。而且kL和kR来控制需要的范围。普遍做法如下:
示例:
二、DiscreteConvolve
DiscreteConvolve是将两个函数做卷积。需要给出函数的表达式,给出的是连续函数的表达式,但是计算时是进行整数点的采样,从而构成一个矩阵,进行计算。这里充分的体现了符号运算的强大之处。用法如下:
DiscreteConvolve[f,g,m,n]表达式 f 和 g 的关于 n 的卷积.
实验如下:(本实验选自《信号与系统》奥本海姆第二版 例2.3
三、Convolve
Convolve[f,g,x,y]计算f和g关于x的卷积。
这个用法相对简单,实验如下:
以下实验选自《信号与系统》奥本海姆第二版例2.7