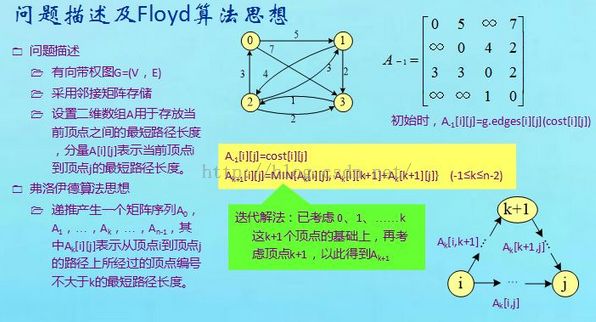
第十三周 Floyd算法验证

/*
* Copyright (c) 2015, 烟台大学计算机与控制工程学院
* All rights reserved.
* 文件名称： main.cpp,top.h,1.cpp
* 作者：于东林
* 完成日期：2015年12月30日
* 版本号：codeblocks
*
* 问题描述:  每对顶点之间的最短路径
* 输入描述： 无
* 程序输出： 见运行结果

*/

程序及代码：

#include <stdio.h>
#include <malloc.h>
#define MAXV 100                //最大顶点个数
#define INF 32767    //INF表示∞
#define MaxSize 100
typedef struct
{
    int u;     //边的起始顶点
    int v;     //边的终止顶点
    int w;     //边的权值
} Edge;

typedef int InfoType;

//以下定义邻接矩阵类型
typedef struct
{
    int no;                     //顶点编号
    InfoType info;              //顶点其他信息，在此存放带权图权值
} VertexType;                   //顶点类型

typedef struct                  //图的定义
{
    int edges[MAXV][MAXV];      //邻接矩阵
    int n,e;                    //顶点数，弧数
    VertexType vexs[MAXV];      //存放顶点信息
} MGraph;                       //图的邻接矩阵类型

//以下定义邻接表类型
typedef struct ANode            //弧的结点结构类型
{
    int adjvex;                 //该弧的终点位置
    struct ANode *nextarc;      //指向下一条弧的指针
    InfoType info;              //该弧的相关信息,这里用于存放权值
} ArcNode;

typedef int Vertex;

typedef struct Vnode            //邻接表头结点的类型
{
    Vertex data;                //顶点信息
    int count;                  //存放顶点入度,只在拓扑排序中用
    ArcNode *firstarc;          //指向第一条弧
} VNode;

typedef VNode AdjList[MAXV];    //AdjList是邻接表类型

typedef struct
{
    AdjList adjlist;            //邻接表
    int n,e;                    //图中顶点数n和边数e
} ALGraph;                      //图的邻接表类型

//功能：由一个反映图中顶点邻接关系的二维数组，构造出用邻接矩阵存储的图
//参数：Arr - 数组名，由于形式参数为二维数组时必须给出每行的元素个数，在此将参数Arr声明为一维数组名（指向int的指针）
//      n - 矩阵的阶数
//      g - 要构造出来的邻接矩阵数据结构
void ArrayToMat(int *Arr, int n, MGraph &g);
void Ppath(int path[][MAXV],int i,int j);
void Dispath(int A[][MAXV],int path[][MAXV],int n);
void Floyd(MGraph g);

#include "top.h"

void ArrayToMat(int *Arr, int n, MGraph &g)
{
    int i,j,count=0;  //count用于统计边数，即矩阵中非0元素个数
    g.n=n;
    for (i=0; i<g.n; i++)
        for (j=0; j<g.n; j++)
        {
            g.edges[i][j]=Arr[i*n+j]; //将Arr看作n×n的二维数组，Arr[i*n+j]即是Arr[i][j]，计算存储位置的功夫在此应用
            if(g.edges[i][j]!=0 && g.edges[i][j]!=INF)
                count++;
        }
    g.e=count;
}

void Ppath(int path[][MAXV],int i,int j)  //前向递归查找路径上的顶点
{
    int k;
    k=path[i][j];
    if (k==-1) return;  //找到了起点则返回
    Ppath(path,i,k);    //找顶点i的前一个顶点k
    printf("%d,",k);
    Ppath(path,k,j);    //找顶点k的前一个顶点j
}
void Dispath(int A[][MAXV],int path[][MAXV],int n)
{
    int i,j;
    for (i=0; i<n; i++)
        for (j=0; j<n; j++)
        {
            if (A[i][j]==INF)
            {
                if (i!=j)
                    printf("从%d到%d没有路径\n",i,j);
            }
            else
            {
                printf("  从%d到%d=>路径长度:%d 路径:",i,j,A[i][j]);
                printf("%d,",i);    //输出路径上的起点
                Ppath(path,i,j);    //输出路径上的中间点
                printf("%d\n",j);   //输出路径上的终点
            }
        }
}
void Floyd(MGraph g)
{
    int A[MAXV][MAXV],path[MAXV][MAXV];
    int i,j,k;
    for (i=0; i<g.n; i++)
        for (j=0; j<g.n; j++)
        {
            A[i][j]=g.edges[i][j];
            path[i][j]=-1;
        }
    for (k=0; k<g.n; k++)
    {
        for (i=0; i<g.n; i++)
            for (j=0; j<g.n; j++)
                if (A[i][j]>A[i][k]+A[k][j])
                {
                    A[i][j]=A[i][k]+A[k][j];
                    path[i][j]=k;
                }
    }
    Dispath(A,path,g.n);   //输出最短路径
}

#include "top.h"
int main()
{
    MGraph g;
    int A[4][4]=
    {
        {0,  5,INF,7},
        {INF,0,  4,2},
        {3,  3,  0,2},
        {INF,INF,1,0}
    };
    ArrayToMat(A[0], 4, g);
    Floyd(g);
    return 0;
}

运行结果：

知识点总结：

       

学习心得:

       知识要学一点当一点，不要丢三落四.