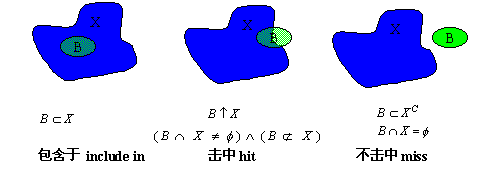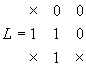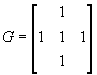数字图像处理：10.形态学运算

1．引言

形态学运算是针对二值图象依据数学形态学(Mathematical Morphology)的集合论方法发展起来的图象处理方法。数学形态学起源于岩相学对岩石结构的定量描述工作，近年来在数字图象处理和机器视觉领域中得到了广泛的应用，形成了一种独特的数字图象分析方法和理论。

通常形态学图象处理表现为一种邻域运算形式，一种特殊定义的邻域称之为“结构元素”（Structure Element），在每个象素位置上它与二值图象对应的区域进行特定的逻辑运算，逻辑运算的结果为输出图象的相应象素。形态学运算的效果取决于结构元素的大小、内容以及逻辑运算的性质。常见的形态学运算有腐蚀(Erosion)和膨胀(Dilation)。

给定二值图象I(x,y)和作为结构元素的二值模板T(i,j)，则典型的腐蚀与膨胀运算可表示成：

腐蚀

膨胀

几种简单对称结构元素（圆形、方形、菱形）如下图所示：

2. 基本概念

（1）包含、击中、不击中

按照集合的概念，给定两个集合：对象（Object）X和结构元素（Structure Element）B，它们之间的关系有如图所示的三种情况：

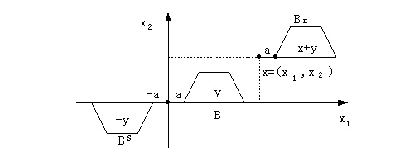
（2）平移、对称集

平移 

对称集（将B旋转180度得到）

（3） 腐蚀

腐蚀是一种消除边界点，使边界向内部收缩的过程。可以用来消除小且无意义的物体。一般意义的腐蚀概念定义为

 

也就是说，由B对X腐蚀所产生的二值图象E是满足以下条件的点(x,y)的集合：如果B的原点平移到点(x,y)，那么B将完全包含于X中。

（4）膨胀

膨胀是将与物体接触的所有背景点合并到该物体中，使边界向外部扩张的过程。可以用来填补物体中的空洞。一般意义的膨胀概念定义为

 

也就是说，由B对X膨胀所产生的二值图象D是满足以下条件的点(x,y)的集合：如果B的原点平移到点(x,y)，那么它与X的交集非空。

性质：对偶关系

例如：

　

另外，腐蚀和膨胀都可以用平移来说明：

　

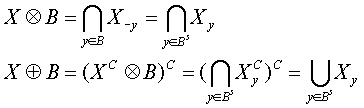例如，在下图中利用圆形结构元素做膨胀运算，填补“细缝”。

（图片来源：艾海舟，王栓，何克忠，基于差分图象的人脸检测，中国图象图形学报，1998; 3(12): 987-992.）

3. 开运算和闭运算

（1）开运算

先腐蚀后膨胀的过程称为开运算。用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。

 

（2）闭运算

先膨胀后腐蚀的过程称为闭运算。用来填充物体内细小空洞、连接邻近物体、平滑其边界的同时并不明显改变其面积。

 

通常，由于噪声的影响，图象在阈值化后所得到边界往往是很不平滑的，物体区域具有一些噪声孔，背景区域上散布着一些小的噪声物体。连续的开和闭运算可以有效地改善这种情况。有时需要经过多次腐蚀之后再加上相同次数的膨胀，才可以产生比较好的效果。

例如：开运算，B₁作用结果：去掉小刺，但未去掉小桥；B₂作用结果：有位移。

　

闭运算，B₁作用结果：去掉小刺，但未去掉小桥；B₂作用结果：去掉小刺，和小桥。

　

4. 击中击不中变换HMT(Hit-Miss Transform)

将形态学运算推广到更为一般的情况，实际上就演变为条件严格的模板匹配。这时结构元素不仅含有物体点，而且还含有背景点，只有当结构元素与所对应的区域完全符合时才作为结果输出到输出图象。

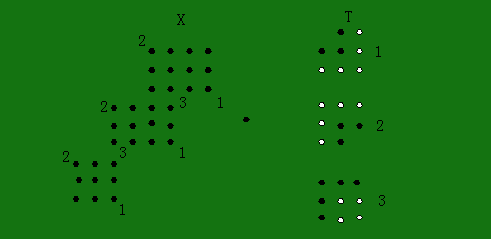
模板T由两部分组成(T₁,T₂), T₁物体点，T₂背景点，HMT定义为

例如，在下图中，对于三个不同的T模板，在X中标出了符合条件的位置。

性质：（1）时，

（2）

4.1细化和粗化

（1）细化（Thin）

细化可以通过逐步去掉满足匹配条件的点的方法来实现，每步运算可表示成：

系统地细化需要考虑一系列的模板，如，其中是旋转的结果（90^º ，180^º ，270^º ）共8种情况。

例如，可用于细化的结构元素有

           

问题：用，是否包含所有可删除的情况？是否包含端点？

具体的细化算法参见第七章（..\chapter07\script07_ahz.htm）。

（2）粗化(Thick)

用点集合,时，

故要选择合适的结构元素，如 

对偶性：（验证一下）

其中，当时，

5. 边界和骨架（Boundary and Skeleton）

边界运算可以用：

抽骨架（Skeletonization）（骨架也称为中轴medial axis）与细化不同主要在于中轴骨架在拐角处延伸到了边界，而细化则不是。抽骨架的一种方法是：

其中

用不同大小的结构元素nG逐步对X腐蚀，直到，每次腐蚀得到宽度和nG成正比的区域段的骨架。

 

以上方法存在一些问题，如有时骨架不连通了，而原区域是连通。一种改进的方法是采用全方形的结构元素

   

演示：..\SourceProgramCodes\chapter9\武勃981403\Debug\ViewDIB.exe

　 Binary Sobel Edge

　Dilation

　Erosion

　Open

　Close

　Thinning by Structure Elemnets of T and L shapes

Form

配套代码实现