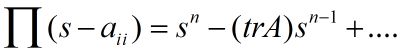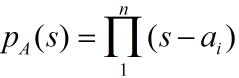- 采购系统功能概述:鲸采云如何通过采购系统帮助企业实现降本增效
鲸采云SRM采购管理系统
人工智能
在全球供应链重构与企业降本增效的双重压力下,传统采购模式正面临前所未有的挑战。数据显示,制造业企业平均因采购流程低效导致成本增加12%,而智能采购系统可帮助企业降低8-15%的采购成本。鲸采云作为新一代智能采购解决方案,通过"AI+采购"深度融合,构建全流程数字化管控体系,已助力超2000家企业实现采购效率提升60%以上。一、智能采购核心功能矩阵:重塑采购管理逻辑供应商管理帮助企业构建涵盖供应商开
- 百度文心大模型 4.5 系列全面开源 英特尔同步支持端侧部署
2025年6月30日,百度如期兑现2月14日的预告,正式开源文心大模型4.5(ERNIE4.5)系列,涵盖10款不同参数规模的模型,包括470亿参数混合专家(MoE)模型、30亿参数MoE模型及3亿参数稠密型模型,实现预训练权重与推理代码的完全开放。这一举措标志着国内大模型技术向生态化、普惠化迈出关键一步。开源矩阵与授权机制:兼顾商业应用与技术共享文心大模型4.5系列基于ApacheLicense
- 【实战派×学院派】30|用户反馈五花八门,优先级怎么排?
郭菁菁
(BA/PM)实战派常踩的坑学院派如何补上大数据BA业务分析需求分析
学院派:用反馈分类体系+Impact-Effort矩阵+路线图对齐机制,让反馈不再靠吵架决定优先级你是不是也遇到过这种场景:“这个问题好多用户在群里抱怨了,能不能先修?”“销售说几个大客户提了建议,最好赶紧做。”“我们自己用着不顺,也想优化下。”结果:反馈源源不断,但每次排优先级时就是:谁声音大、谁能找到领导,谁的需求就往前排。✅实战派常见误区:靠“印象流”排优先级实战派习惯做法潜在问题结果谁催得
- 程序人生:技术人如何实现职业阶梯的跨越式发展
AI天才研究院
AI大模型企业级应用开发实战AgenticAI实战AI人工智能与大数据程序人生职场和发展ai
程序人生:技术人如何实现职业阶梯的跨越式发展关键词:职业发展、技术领导力、T型人才、职业规划、跨领域能力、持续学习、技术管理摘要:本文针对技术从业者的职业发展痛点,构建了系统化的职业阶梯跨越模型。通过解析技术人才成长的核心阶段与能力模型,结合数学量化评估体系和实战案例,提供从技术深耕到领导力跃迁的完整路径。内容涵盖能力矩阵构建、项目实战策略、跨领域知识融合、个人品牌经营等关键模块,帮助技术人突破职
- 服务器异常宕机或重启导致 RabbitMQ 启动失败问题分析与解决方案
代码怪兽大作战
RabbitMQ服务器rabbitmq宕机启动失败
服务器异常宕机或重启导致RabbitMQ启动失败问题分析与解决方案一、深度故障诊断与解决方案1.权限配置不当故障2.端口占用故障3.数据目录残留故障二、故障类型对比与诊断矩阵三、完整恢复流程(10步法)四、风险规避与最佳实践️数据保护策略预防性配置五、高级故障排除技巧诊断工具集容器特有故障处理容器维护命令速查主机与容器方案对比总结⚡快速恢复决策树六、总结当服务器异常宕机或重启后,RabbitMQ启
- 从零实现Llama3:深入解析Transformer架构与实现细节
祁婉菲Flora
从零实现Llama3:深入解析Transformer架构与实现细节llama3-from-scratchllama3一次实现一个矩阵乘法。项目地址:https://gitcode.com/gh_mirrors/ll/llama3-from-scratch引言本文将深入探讨如何从零开始实现Llama3语言模型。我们将从最基本的张量操作开始,逐步构建完整的Transformer架构。通过这个过程,读者
- pytorch小记(二十六):全面解读 PyTorch 的 `torch.matmul`
pytorch小记(二十六):全面解读PyTorch的`torch.matmul`PyTorch中的`torch.matmul`详解与使用指南一、什么是`torch.matmul`二、基本用法示例1.向量点积(1-D×1-D)2.二维矩阵乘法(2-D×2-D)3.批量矩阵乘法(≥3-D)4.向量与矩阵混合三、与`mm`、`bmm`的区别四、性能与数值稳定性五、典型应用场景六、注意事项七、总结在深度
- 【unitrix】 4.12 通用2D仿射变换矩阵(matrix/types.rs)
liuyuan77
我的unitrix库rust
一、源码这段代码定义了一个通用的2D仿射变换矩阵结构,可用于表示二维空间中的各种线性变换。///通用2D仿射变换矩阵(元素仅需实现Copytrait)//////该矩阵可用于表示二维空间中的任意仿射变换,支持以下应用场景:///1.平面几何转换(平移/旋转/缩放/剪切)///2.颜色空间线性变换(如RGB到YUV转换)///3.带物理单位的量值转换(如像素到毫米的映射)///4.动画系统中的插值变
- 理想运算放大器的神话与现实:若完美存在,电子世界将如何颠覆?
理想运算放大器(IdealOperationalAmplifier)是电子工程教材中的“完美模型”,它定义了模拟电路设计的理论基石。但若这种完美器件真实存在,整个电子产业将被彻底重构——本章将揭示理想运放的深层特性,并推演其可能引发的技术革命。一、理想运算放大器的终极定义1.1核心特性矩阵理想运放需同时满足以下五个极限条件:开环增益:AOL=∞A_{OL}=\inftyAOL=∞输入阻抗:Zin=
- 西南交通大学【机器学习实验1】
实验目的理解和掌握回归问题和分类问题模型评估方法,学会使用均方误差、最大绝对误差、均方根误差指标评估回归模型,学会使用错误率、精度、查全率、查准率、F1指标评价分类模型。实验内容给定回归问题的真实标签和多个算法的预测结果,编程实现MSE、MAE、RMSE三种评测指标,对模型进行对比分析。给定二分类问题真实标签和多个算法的预测结果,编程实现混淆矩阵评测,采用错误率、精度、查全率、查准率、F1指标对结
- 用sklearn库中的算法对数据集进行训练和auc评估(个人学习笔记)
ZD困困困
python机器学习
本文为个人学习笔记,仅供学习参考,欢迎讨论,要是有哪里写的不对或有疑问的欢迎讨论。题目:运用已给数据集进行模型训练,使用逻辑回归、决策树、随机森林和AdaBoost几个算法进行训练,并打印各个算法训练后的auc评价指标。文章目录1.导入数据集①read_csv():读取数据并以某字符分隔。②merge():合并③drop():删除行或列④tolist():将数组或矩阵转换为列表⑤train_tes
- 数字人矩阵源码--基于深度学习的数字人面部表情合成
我~18339948121
数字人源码数字人矩阵源码123数字人源码矩阵深度学习线性代数人工智能flasktornadopython
AI正在席卷全球,数字人市场需求增长,用AI数字分身一天就能生产出几十条高质量短视频,你只需要上传一段视频,甚至都不用开口说话,直接复制粘贴文案,就能得到一个属于你的数字分身。深度学习数字人面部表情合成的关键技术3D面部建模与参数化建立高精度3D面部模型是表情合成的基础,常用Blendshape或面部动作编码系统(FACS)作为参数化控制方法。Blendshape通过线性组合基础表情形状生成新表情
- Jenkins Pipeline共享库配置错误深度解析与修复实战
喜欢编程就关注我
jenkins运维Pipeline共享库配置错误深度解析与修复实战代码
JenkinsPipeline共享库配置错误深度解析与修复实战一、共享库配置错误全景图谱1.1经典错误日志矩阵错误类型典型报错特征触发场景诊断关键点仓库克隆失败FailedtoclonerepositoryGit/SVN仓库地址错误/权限不足网络连通性/凭证配置符号解析失败unabletoresolveclass变量作用域错误/未正确导入类共享库加载顺序/命名空间冲突版本兼容性问题NosuchDS
- 《二分枚举答案(配合经典算法)》题集
英雄哪里出来
算法数据结构英雄算法联盟二分
文章目录1、模板题集2、课内题集3、课后题集1.差分2.贪心/排序3.二维前缀和4.K大数5.BFS6.最短路7.数位DP1、模板题集分巧克力2、课内题集倒水冶炼金属连续子序列的个数3、课后题集括号内的整数代表完整代码行数。1.差分粉刷小能手小蓝(42)操作数组的最小次数(43)森林的最大美丽值(44)2.贪心/排序信号塔(33)可得到的最大团队默契(35)3.二维前缀和小秋的矩阵(48)4.K大
- STM32 驱动矩阵键盘详解与完整示例
深入黑暗
单片机开发stm32矩阵嵌入式硬件单片机驱动开发
STM32驱动矩阵键盘详解与完整示例矩阵键盘在嵌入式开发中是一种常见的输入设备,广泛应用于工业控制、人机界面、消费电子等领域。本文将详细介绍如何在STM32平台上驱动一个4x4矩阵键盘,涵盖原理分析、硬件连接、软件编程、防抖处理、问题排查与优化技巧等,适合初学者和进阶用户参考。一、矩阵键盘基本原理1.1什么是矩阵键盘?矩阵键盘是将按键按行列排布形成网格状结构的键盘,通过行线(Row)和列线(Col
- 面试150 旋转图像
Alfred king
面试150题目面试leetcode数组
思路解包法。zip函数可以使矩阵转置,本题需要对矩阵先反转在转置。因此联想到zip是一种很简便的方法classSolution:defrotate(self,matrix:List[List[int]])->None:"""Donotreturnanything,modifymatrixin-placeinstead."""matrix[:]=zip(*matrix[::-1])
- Python爬虫(57)Python数据可视化全攻略:Matplotlib从入门到三维动态图表(8000字实战教程)
一个天蝎座白勺程序猿
Python爬虫入门到高阶实战python爬虫信息可视化
目录背景与需求分析第一章:Matplotlib基础与核心工作流1.1环境配置与基础架构1.2基础图表类型实战1.2.1折线图进阶1.2.2分组柱状图第二章:高阶可视化技术2.1子图矩阵与多面板布局2.2动态可视化与动画第三章:行业案例实战案例1:电商用户行为分析案例2:医疗影像数据可视化第四章:可视化美学与工程优化4.1配色方案实战4.2百万级数据渲染优化第五章:交互式扩展方案5.1Matplot
- 基于STM32F103C8T6实现的矩阵键盘
嗜好的学习记录
stm32单片机嵌入式硬件
基于STM32F103RC系列矩阵键供大家复制粘贴和使用。本章只对有基础的同学方便复制,也简单易懂接线图:A4--A5--A6--A7||||A0---+-----+------+------+||||A1---+-----+------+------+||||A2---+------+------+------+||||A3---+------+------+-----+返回值对应表:A4---
- 【数据标注师】语音校对标注
试着
数据标注师语音识别人工智能数据标注师语音校对标注
目录一、语音校对标注的核心使命**任务本质****四大核心价值**二、专业工作环境配置**硬件黄金组合****软件栈深度掌握**三、九大错误类型识别与修正**语音校对错误矩阵**四、专业校对工作流**五步双轨校对法****复杂场景攻坚策略五、质量与效率的平衡术**质检三维度****效率提升方案**六、领域专业化路径**医疗语音校对专精****法律语音校对专精**七、职业进阶方向**能力跃迁模型**
- 海外社交App开发实战:从0到百万DAU的架构设计
VI8664956I26
java
一、海外社交赛道破局点:找到你的“社交原子习惯”新兴市场机会矩阵地区用户痛点成功案例东南亚线下社交成本高Litmatch(匿名语音匹配)中东性别隔离文化下的匿名需求Yalla(语音聊天室)拉美热情文化+高移动渗透率Badoo(附近的人)功能设计黄金公式社交动力=低门槛互动×即时反馈×身份认同反例:要求填写10项资料才能聊天→用户流失率↑80%正例:Soul的“灵魂测试”→3步生成虚拟身份二、核心技
- leedcode:最大人工岛
卖报的火柴人
算法java
题目:给你一个大小为nxn二进制矩阵grid。最多只能将一格0变成1。返回执行此操作后,grid中最大的岛屿面积是多少?岛屿由一组上、下、左、右四个方向相连的1形成classSolution{publicintlargestIsland(int[][]grid){MapmapIndexLand=newHashMap();//陆地的编号intindex=2;//先标记出岛屿//循环行for(inti
- 【力扣—剑指 Offer(第 2 版)简单题目解析汇总】
Wupke
剑指offer数据结构与算法学习LeetCodeleetcode剑指offer数据结构与算法
【力扣—剑指Offer(第2版)简单题目解析汇总】说明1、基本字符串数组数组-排序矩阵/模拟枚举2、算法动态规划深度优先搜索广度优先搜索递归分治记忆化搜索快速选择二分查找3、基础数据结构树(二叉树)二叉搜索树栈队列堆(优先队列)哈希表链表4、技巧性题目双指针位运算计数设计说明简单题目共计38道,按照标签分类为:基本、算法、基础数据结构、技巧等,具体如下。1、基本字符串剑指Offer05.替换空格.
- 力扣74 搜索二维矩阵
许愿与你永世安宁
力扣刷题笔记leetcode矩阵算法
获取矩阵的行数和列数vector>&matrixmatrix是一个vector>类型的二维向量,其本质是一个嵌套的动态数组matrix.size()返回的是外层vector的大小,即有多少个vector元素,也就是二维向量的行数matrix[0]是第一行的vector,即第一个vector元素matrix[0].size()返回第一行的大小,也就是该行中int元素的数量,即列数一维索引与二维坐标的
- 《高等代数》线性相关和线性无关无关典型例题
代码小白菜菜
高等代数笔记高等代数
说明:此文章用于本人复习巩固,如果也能帮到大家那就更加有意义了。注:1)一般情况下题目要求证明哪个向量组线性相关或线性无关就用线性相关和线性无关的定义将等式写出来,然后再用适当的方法进行求解。2)在这题中,利用了行列式有解无解和线性相关和线性无关的关系进行判断是线性相关还是线性无关。
- 如何选择合适的IP轮换周期
IP管家
tcp/ip网络协议网络网络安全ip
选择合适的IP轮换周期需综合业务目标、目标平台风控规则、IP类型与质量等多维度因素,以下是系统化决策框架及实操建议:一、核心决策要素业务场景类型高频操作型(如数据采集、广告点击):轮换周期短(30秒~5分钟),避免单IP请求过密触发反爬。示例:电商比价监控建议每30-60分钟更换IP。长期运营型(如社交媒体、账号矩阵):轮换周期长(6~12小时),维持会话稳定性。示例:TikTok账号运营每6-1
- Python 数据分析与机器学习入门 (三):Pandas 数据导入与核心操作
程序员阿超的博客
Pythonpython数据分析机器学习PandasDataFrameSeries数据清洗
引言:Pandas是什么,为何如此重要?如果说NumPy是处理原始数值数组的利器,那么Pandas则是驾驭结构化数据的瑞士军刀。在真实世界的数据分析项目中,数据很少是单纯的数字矩阵。它们通常以表格形式存在,包含行和列,每列可能有不同的数据类型(如文本、数字、日期),并且带有描述性的列名和行索引。Pandas正是为高效处理这类数据而生。Pandas构建于NumPy之上,它不仅继承了NumPy的高性能
- 代码随想录|图论|07岛屿的最大面积
Paper Clouds
算法深度优先图论数据结构c++
leetcode:100.岛屿的最大面积题目题目描述给定一个由1(陆地)和0(水)组成的矩阵,计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。输入描述第一行包含两个整数N,M,表示矩阵的行数和列数。后续N行,每行包含M个数字,数字为1或者0,表示岛屿的单元格。输出描述输出一个整数,表示岛屿的最
- 代码随想录: 图论| 岛屿数量
王鹏程_
深度优先算法岛屿数量图论
题目链接:99.岛屿数量题目描述:给定一个由1(陆地)和0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。输入描述:第一行包含两个整数N,M,表示矩阵的行数和列数。后续N行,每行包含M个数字,数字为1或者0。输出描述:输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出0。输入示例:4511000110000010
- LeetCode LCP 68.美观的花束
吃着火锅x唱着歌
LeetCodeleetcode算法职场和发展
力扣嘉年华的花店中从左至右摆放了一排鲜花,记录于整型一维矩阵flowers中每个数字表示该位置所种鲜花的品种编号。你可以选择一段区间的鲜花做成插花,且不能丢弃。在你选择的插花中,如果每一品种的鲜花数量都不超过cnt朵,那么我们认为这束插花是「美观的」。例如:[5,5,5,6,6]中品种为5的花有3朵,品种为6的花有2朵,每一品种的数量均不超过3请返回在这一排鲜花中,共有多少种可选择的区间,使得插花
- Python隐式反馈数据集库之implicit使用详解
Rocky006
python开发语言
概要Implicit是一个专注于隐式反馈数据集的协同过滤推荐系统Python库,由BenFrederickson开发。与显式反馈(如用户明确给予的评分)不同,隐式反馈是指用户通过行为间接表达偏好的数据,如点击次数、浏览时长或购买历史。这类数据在实际应用中更为普遍,但也更难以处理。传统推荐系统如Surprise或LightFM虽然功能全面,但在处理大规模稀疏矩阵时性能不佳。Implicit库通过优化
- 项目中 枚举与注解的结合使用
飞翔的马甲
javaenumannotation
前言:版本兼容,一直是迭代开发头疼的事,最近新版本加上了支持新题型,如果新创建一份问卷包含了新题型,那旧版本客户端就不支持,如果新创建的问卷不包含新题型,那么新旧客户端都支持。这里面我们通过给问卷类型枚举增加自定义注解的方式完成。顺便巩固下枚举与注解。
一、枚举
1.在创建枚举类的时候,该类已继承java.lang.Enum类,所以自定义枚举类无法继承别的类,但可以实现接口。
- 【Scala十七】Scala核心十一:下划线_的用法
bit1129
scala
下划线_在Scala中广泛应用,_的基本含义是作为占位符使用。_在使用时是出问题非常多的地方,本文将不断完善_的使用场景以及所表达的含义
1. 在高阶函数中使用
scala> val list = List(-3,8,7,9)
list: List[Int] = List(-3, 8, 7, 9)
scala> list.filter(_ > 7)
r
- web缓存基础:术语、http报头和缓存策略
dalan_123
Web
对于很多人来说,去访问某一个站点,若是该站点能够提供智能化的内容缓存来提高用户体验,那么最终该站点的访问者将络绎不绝。缓存或者对之前的请求临时存储,是http协议实现中最核心的内容分发策略之一。分发路径中的组件均可以缓存内容来加速后续的请求,这是受控于对该内容所声明的缓存策略。接下来将讨web内容缓存策略的基本概念,具体包括如如何选择缓存策略以保证互联网范围内的缓存能够正确处理的您的内容,并谈论下
- crontab 问题
周凡杨
linuxcrontabunix
一: 0481-079 Reached a symbol that is not expected.
背景:
*/5 * * * * /usr/IBMIHS/rsync.sh
- 让tomcat支持2级域名共享session
g21121
session
tomcat默认情况下是不支持2级域名共享session的,所有有些情况下登陆后从主域名跳转到子域名会发生链接session不相同的情况,但是只需修改几处配置就可以了。
打开tomcat下conf下context.xml文件
找到Context标签,修改为如下内容
如果你的域名是www.test.com
<Context sessionCookiePath="/path&q
- web报表工具FineReport常用函数的用法总结(数学和三角函数)
老A不折腾
Webfinereport总结
ABS
ABS(number):返回指定数字的绝对值。绝对值是指没有正负符号的数值。
Number:需要求出绝对值的任意实数。
示例:
ABS(-1.5)等于1.5。
ABS(0)等于0。
ABS(2.5)等于2.5。
ACOS
ACOS(number):返回指定数值的反余弦值。反余弦值为一个角度,返回角度以弧度形式表示。
Number:需要返回角
- linux 启动java进程 sh文件
墙头上一根草
linuxshelljar
#!/bin/bash
#初始化服务器的进程PId变量
user_pid=0;
robot_pid=0;
loadlort_pid=0;
gateway_pid=0;
#########
#检查相关服务器是否启动成功
#说明:
#使用JDK自带的JPS命令及grep命令组合,准确查找pid
#jps 加 l 参数,表示显示java的完整包路径
#使用awk,分割出pid
- 我的spring学习笔记5-如何使用ApplicationContext替换BeanFactory
aijuans
Spring 3 系列
如何使用ApplicationContext替换BeanFactory?
package onlyfun.caterpillar.device;
import org.springframework.beans.factory.BeanFactory;
import org.springframework.beans.factory.xml.XmlBeanFactory;
import
- Linux 内存使用方法详细解析
annan211
linux内存Linux内存解析
来源 http://blog.jobbole.com/45748/
我是一名程序员,那么我在这里以一个程序员的角度来讲解Linux内存的使用。
一提到内存管理,我们头脑中闪出的两个概念,就是虚拟内存,与物理内存。这两个概念主要来自于linux内核的支持。
Linux在内存管理上份为两级,一级是线性区,类似于00c73000-00c88000,对应于虚拟内存,它实际上不占用
- 数据库的单表查询常用命令及使用方法(-)
百合不是茶
oracle函数单表查询
创建数据库;
--建表
create table bloguser(username varchar2(20),userage number(10),usersex char(2));
创建bloguser表,里面有三个字段
&nbs
- 多线程基础知识
bijian1013
java多线程threadjava多线程
一.进程和线程
进程就是一个在内存中独立运行的程序,有自己的地址空间。如正在运行的写字板程序就是一个进程。
“多任务”:指操作系统能同时运行多个进程(程序)。如WINDOWS系统可以同时运行写字板程序、画图程序、WORD、Eclipse等。
线程:是进程内部单一的一个顺序控制流。
线程和进程
a. 每个进程都有独立的
- fastjson简单使用实例
bijian1013
fastjson
一.简介
阿里巴巴fastjson是一个Java语言编写的高性能功能完善的JSON库。它采用一种“假定有序快速匹配”的算法,把JSON Parse的性能提升到极致,是目前Java语言中最快的JSON库;包括“序列化”和“反序列化”两部分,它具备如下特征:
- 【RPC框架Burlap】Spring集成Burlap
bit1129
spring
Burlap和Hessian同属于codehaus的RPC调用框架,但是Burlap已经几年不更新,所以Spring在4.0里已经将Burlap的支持置为Deprecated,所以在选择RPC框架时,不应该考虑Burlap了。
这篇文章还是记录下Burlap的用法吧,主要是复制粘贴了Hessian与Spring集成一文,【RPC框架Hessian四】Hessian与Spring集成
- 【Mahout一】基于Mahout 命令参数含义
bit1129
Mahout
1. mahout seqdirectory
$ mahout seqdirectory
--input (-i) input Path to job input directory(原始文本文件).
--output (-o) output The directory pathna
- linux使用flock文件锁解决脚本重复执行问题
ronin47
linux lock 重复执行
linux的crontab命令,可以定时执行操作,最小周期是每分钟执行一次。关于crontab实现每秒执行可参考我之前的文章《linux crontab 实现每秒执行》现在有个问题,如果设定了任务每分钟执行一次,但有可能一分钟内任务并没有执行完成,这时系统会再执行任务。导致两个相同的任务在执行。
例如:
<?
//
test
.php
- java-74-数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字
bylijinnan
java
public class OcuppyMoreThanHalf {
/**
* Q74 数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字
* two solutions:
* 1.O(n)
* see <beauty of coding>--每次删除两个不同的数字,不改变数组的特性
* 2.O(nlogn)
* 排序。中间
- linux 系统相关命令
candiio
linux
系统参数
cat /proc/cpuinfo cpu相关参数
cat /proc/meminfo 内存相关参数
cat /proc/loadavg 负载情况
性能参数
1)top
M:按内存使用排序
P:按CPU占用排序
1:显示各CPU的使用情况
k:kill进程
o:更多排序规则
回车:刷新数据
2)ulimit
ulimit -a:显示本用户的系统限制参
- [经营与资产]保持独立性和稳定性对于软件开发的重要意义
comsci
软件开发
一个软件的架构从诞生到成熟,中间要经过很多次的修正和改造
如果在这个过程中,外界的其它行业的资本不断的介入这种软件架构的升级过程中
那么软件开发者原有的设计思想和开发路线
- 在CentOS5.5上编译OpenJDK6
Cwind
linuxOpenJDK
几番周折终于在自己的CentOS5.5上编译成功了OpenJDK6,将编译过程和遇到的问题作一简要记录,备查。
0. OpenJDK介绍
OpenJDK是Sun(现Oracle)公司发布的基于GPL许可的Java平台的实现。其优点:
1、它的核心代码与同时期Sun(-> Oracle)的产品版基本上是一样的,血统纯正,不用担心性能问题,也基本上没什么兼容性问题;(代码上最主要的差异是
- java乱码问题
dashuaifu
java乱码问题js中文乱码
swfupload上传文件参数值为中文传递到后台接收中文乱码 在js中用setPostParams({"tag" : encodeURI( document.getElementByIdx_x("filetag").value,"utf-8")});
然后在servlet中String t
- cygwin很多命令显示command not found的解决办法
dcj3sjt126com
cygwin
cygwin很多命令显示command not found的解决办法
修改cygwin.BAT文件如下
@echo off
D:
set CYGWIN=tty notitle glob
set PATH=%PATH%;d:\cygwin\bin;d:\cygwin\sbin;d:\cygwin\usr\bin;d:\cygwin\usr\sbin;d:\cygwin\us
- [介绍]从 Yii 1.1 升级
dcj3sjt126com
PHPyii2
2.0 版框架是完全重写的,在 1.1 和 2.0 两个版本之间存在相当多差异。因此从 1.1 版升级并不像小版本间的跨越那么简单,通过本指南你将会了解两个版本间主要的不同之处。
如果你之前没有用过 Yii 1.1,可以跳过本章,直接从"入门篇"开始读起。
请注意,Yii 2.0 引入了很多本章并没有涉及到的新功能。强烈建议你通读整部权威指南来了解所有新特性。这样有可能会发
- Linux SSH免登录配置总结
eksliang
ssh-keygenLinux SSH免登录认证Linux SSH互信
转载请出自出处:http://eksliang.iteye.com/blog/2187265 一、原理
我们使用ssh-keygen在ServerA上生成私钥跟公钥,将生成的公钥拷贝到远程机器ServerB上后,就可以使用ssh命令无需密码登录到另外一台机器ServerB上。
生成公钥与私钥有两种加密方式,第一种是
- 手势滑动销毁Activity
gundumw100
android
老是效仿ios,做android的真悲催!
有需求:需要手势滑动销毁一个Activity
怎么办尼?自己写?
不用~,网上先问一下百度。
结果:
http://blog.csdn.net/xiaanming/article/details/20934541
首先将你需要的Activity继承SwipeBackActivity,它会在你的布局根目录新增一层SwipeBackLay
- JavaScript变换表格边框颜色
ini
JavaScripthtmlWebhtml5css
效果查看:http://hovertree.com/texiao/js/2.htm代码如下,保存到HTML文件也可以查看效果:
<html>
<head>
<meta charset="utf-8">
<title>表格边框变换颜色代码-何问起</title>
</head>
<body&
- Kafka Rest : Confluent
kane_xie
kafkaRESTconfluent
最近拿到一个kafka rest的需求,但kafka暂时还没有提供rest api(应该是有在开发中,毕竟rest这么火),上网搜了一下,找到一个Confluent Platform,本文简单介绍一下安装。
这里插一句,给大家推荐一个九尾搜索,原名叫谷粉SOSO,不想fanqiang谷歌的可以用这个。以前在外企用谷歌用习惯了,出来之后用度娘搜技术问题,那匹配度简直感人。
环境声明:Ubu
- Calender不是单例
men4661273
单例Calender
在我们使用Calender的时候,使用过Calendar.getInstance()来获取一个日期类的对象,这种方式跟单例的获取方式一样,那么它到底是不是单例呢,如果是单例的话,一个对象修改内容之后,另外一个线程中的数据不久乱套了吗?从试验以及源码中可以得出,Calendar不是单例。
测试:
Calendar c1 =
- 线程内存和主内存之间联系
qifeifei
java thread
1, java多线程共享主内存中变量的时候,一共会经过几个阶段,
lock:将主内存中的变量锁定,为一个线程所独占。
unclock:将lock加的锁定解除,此时其它的线程可以有机会访问此变量。
read:将主内存中的变量值读到工作内存当中。
load:将read读取的值保存到工作内存中的变量副本中。
- schedule和scheduleAtFixedRate
tangqi609567707
javatimerschedule
原文地址:http://blog.csdn.net/weidan1121/article/details/527307
import java.util.Timer;import java.util.TimerTask;import java.util.Date;
/** * @author vincent */public class TimerTest {
- erlang 部署
wudixiaotie
erlang
1.如果在启动节点的时候报这个错 :
{"init terminating in do_boot",{'cannot load',elf_format,get_files}}
则需要在reltool.config中加入
{app, hipe, [{incl_cond, exclude}]},
2.当generate时,遇到:
ERROR