复杂链表的复制

Q:有一个复杂链表，其结点除了有一个m_pNext指针指向下一个结点外，还有一个m_pSibling指向链表中的任一结点或者NULL。请完成函数ComplexNode* Clone(ComplexNode* pHead)，以复制一个复杂链表。

A:一开始想这道题毫无思路，如果蛮来，首先创建好正常的链表，然后考虑sibling这个分量，则需要O(n^2)的时间复杂度，然后一个技巧便可以巧妙的解答此题。看图便知。

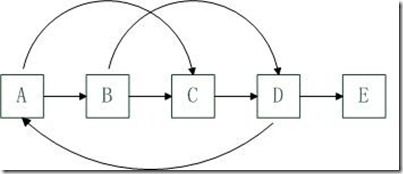
首先是原始的链表

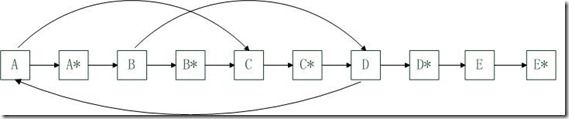
然后我们还是首先复制每一个结点N为N*，不同的是我们将N*让在对应的N后面，即为

然后我们要确定每一个N*的sibling分量，非常明显，N的sibling分量的next就是N*的sibling分量。

最后，将整个链表拆分成原始链表和拷贝出的链表。

这样，我们就解决了一个看似非常混乱和复杂的问题。

struct  Node
{
    int  val;
    Node* next;
    Node* sibling;
};
void  Clone(Node* head)
{
    Node* current=head;
    while (current)
    {
        Node* temp= new  Node;
        temp->val=current->val;
        temp->next=current->next;
        temp->sibling=NULL;
        current->next=temp;
        current=temp->next;
    }
}


void  ConstructSibling(Node* head)
{
    Node* origin=head;
    Node* clone;
    while (origin)
    {
        clone=origin->next;
        if (origin->sibling)
            clone->sibling=origin->sibling->next;
        origin=clone->next;
    }
}

Node* Split(Node* head)
{
    Node *CloneHead,*clone,*origin;
    origin=head;
    if (origin)
    {
        CloneHead=origin->next;
        origin->next=CloneHead->next;
        origin=CloneHead->next;
        clone=CloneHead;
    }
    while (origin)
    {
        Node* temp=origin->next;
        origin->next=temp->next;
        origin=origin->next;
        clone->next=temp;
        clone=temp;
    }
    return  CloneHead;
}


//the whole thing
Clone(head);
ConstructSibling(head);
return  Split(head);