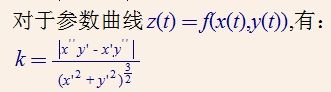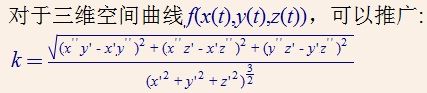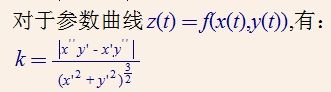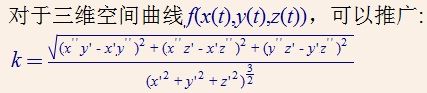- 工业控制系统的8种类型
dotNET跨平台
工业控制系统(ICS)是指用于操作或自动化常见工业过程的任何设备、网络或系统及其相关仪表的统称。ICS几乎被所有工业领域和关键基础设施行业使用,包括但不限于能源、制造、运输和污水处理。工业控制系统有几种类型。它们在大小和复杂性上有所不同,并且是为不同的行业和不同的任务设计的。最常见的包括监督控制和数据采集(SCADA)系统、分布式控制系统(DCS)、可编程逻辑控制器(PLC)以及其他几种。继续阅读
- Spread.NET 18.0 支持.NET9.0 Crack
sdk大全
Spread.NETSpread.NET
Spread.NET全球销量第一的C#.NET电子表格,包含500多个Excel函数在C#.NET中提供真正类似Excel的电子表格体验,且不依赖Excel。创建财务、预算/预测、科学、工程、医疗保健、保险、教育、制造和许多其他类似的业务应用程序。使用全面的API创建企业电子表格、高级网格、仪表板、报告和数据输入表单递送类似Excel的电子表格经验,快速利用强大的高速计算引擎完成最复杂的计算导入和
- 低空经济市场竞争激烈,无人机研发公司如何突破困境?
无人机技术圈
无人机技术无人机
低空经济是指以民用有人驾驶和无人驾驶航空器为主,以载人、载货及其他作业等多场景低空飞行活动为牵引,辐射带动相关领域融合发展的综合性经济形态。从应用场景来看,低空经济涉及军用、政用、商用、民用全方位场景;从产品角度来看,主要包含低空内飞行的无人机、私人飞机、eVTOL等航空器;从产业构成来看,主要包括低空制造、低空飞行、低空保障、低空基础设施和综合服务等产业。在低空经济市场竞争激烈的背景下,无人机研
- 附原文 |《2024年漏洞与威胁趋势报告》深度解读
漏洞
在信息技术飞速发展的当下,网络安全已然成为全球瞩目的焦点。安全极客社区精心译制的《2024年漏洞与威胁趋势报告》明确指出,2023年堪称网络安全领域的重要分水岭。这一年,新发现漏洞的数量出现了前所未有的增长态势,其中高危或严重级别的漏洞占比高达一半,漏洞利用的时间线显著缩短,然而平均修复时间却过长。金融服务、制造业以及公用事业等行业面临的网络威胁愈发严峻,首席信息安全官所承担的法律责任也日益加重。
- 星环科技×鼎捷软件强强联手,共建数智制造新引擎
人工智能
近日,星环科技与鼎捷软件基于雅典娜新型工业互联网平台强强联手,围绕制造业普遍面临的生产计划、过程控制、成本管理等环节存在的经营痛点,以数据为核心打造工业互联网平台,从关键生产流程入手,建立了实时、系统、全面的数据采集工艺流程,驱动研发、生产、制造、销售、服务等环节创造更大的价值,共同推进制造业数字化转型。鼎捷雅典娜是一款以数据思维为引领的新型工业互联网平台,通过数智驱动、任务领航,致力于协助企业实
- 无人机桨叶数量设计科普!
云卓SKYDROID
无人机云卓科技科普高科技桨叶
一、无人机桨叶数量的设计两叶桨:结构简单,重量轻,易于制造和维护。空气阻力相对较小,有利于提高飞行速度和续航时间。适用于轻型无人机或对推力要求不高的应用场景。三叶桨:相比两叶桨,三叶桨在提供更大推力的同时,也能保持较好的空气动力学性能。广泛应用于需要一定负载能力的无人机,如FPV(穿越机)等。三叶桨的平衡性较好,有助于减少飞行中的振动和噪音。四叶桨及以上:桨叶数量增加,推力显著提升,适合重载无人机
- 供应链管理新境界:SCM如何促进信息共享与高效合作
团队协作
一、SCM是什么SCM,全称SupplyChainManagement,即供应链管理,是一种集成化的管理思想和方法,它执行供应链中从供应商到最终用户的物流的计划和控制等职能。SCM涵盖了从供应商到制造商、分销商、零售商,直到最终用户的整个过程中商品、服务以及信息的流动和转换。在SCM中,企业努力将顾客所需的正确的产品(RightProduct)能够在正确的时间(RightTime)、按照正确的数量
- 电商项目管理优化新视角:看板的实战智慧与策略
团队协作团队协作工具
在电商行业,项目管理是企业运营的核心环节之一,它直接关系到企业的运营效率、市场竞争力和长期发展。随着市场需求的快速变化和竞争的日益激烈,电商企业需要不断探索和实践新的项目管理方法,以提升自身的竞争力。看板管理作为一种直观、高效的项目管理工具,为电商项目管理带来了新的视角和智慧。一、看板管理的概念与特点看板管理源自制造业,是一种精益生产方式,旨在通过可视化的方式来管理工作和流程。其核心在于,通过对每
- 《全星 QMS 软件系统》——制造业质量管理的得力助手!
APQP枫枫
汽车部件质量管理QMS软件汽车制造低代码
《全星QMS软件系统》——制造业质量管理的得力助手!在当今竞争激烈、变化万千的市场环境中,产品质量无疑是企业生存发展的坚固基石。质量的优劣直接决定着企业的兴衰成败,影响着其在市场中的地位和声誉。《全星QMS软件系统》恰如一位智慧而可靠的伙伴,助力企业提升质量管理水平,主要表现如下专业性强:《全星QMS软件系统》深耕于制造业质量管理领域,宛如一位经验丰富的专家。它对行业的痛点有着敏锐而深刻的洞察,例
- 什么是工业4.0?
lynn-fish
工业4.0智能制造智能化物联网智能工厂制造数字化转型
在当今这个日新月异的时代,科技的每一次飞跃都深刻地改变着我们的生活与工作方式。而在这场全球性的变革中,工业4.0不仅代表了制造业的未来趋势,更是全球经济发展的新引擎。那么,究竟什么是工业4.0?它如何重塑我们的工业体系,又将带来哪些前所未有的机遇与挑战?一、工业4.0的定义工业4.0,也被称为第四次工业革命,是信息技术与制造业深度融合的产物。它起源于2011年德国提出的高科技战略项目,旨在通过计算
- 开源项目怎么搞钱 · 上
原文地址开源意味着给自己制造随处潜伏的竞争对手,以及花费大量时间评估和解决问题。那么为什么不建立一个封闭源代码的SaaS呢?以下是我遇到的一些开源理由:起源于工作需要很多开源项目最初都是解决公司特定问题的库。这也是Sentry的创始人DavidCramer的创始故事《Sentry:从零开始》中真实发生的。Disquswasalsoanenablertomyopensourcecontributio
- Soc简介
IC开源世界
硬件工程
SoC即系统级芯片又称片上系统(SoC,SystemonChip)。SoC将系统的主要功能综合到一块芯片中,本质上是在做一种复杂的IC设计。SoC是集成电路设计和制造工艺发展的产物,它可以将整个系统集成在一个芯片上。SoC按用途可分为两种类型:一种是专用SoC芯片,是专用集成电路(ASIC)向系统级集成的自然发展;另一种是通用SoC芯片,将绝大部分部件,如CPU、DSP、RAM、I/O等集成在芯片
- 质量管理全星 QMS 软件系统:赋能制造业高品质产品管理
APQP枫枫
汽车制造低代码车载系统
全星QMS软件系统:赋能制造业高品质产品管理在当今竞争激烈的制造业市场中,高品质的产品是企业立足之本。全星QMS软件系统作为一款先进的质量管理软件,为制造业企业提供了全方位、高效能的品质管理解决方案,助力企业打造高品质产品,提升市场竞争力。一、全面覆盖质量管理各环节全星QMS软件系统贯穿产品全生命周期,从原材料采购到产品交付售后,实现无缝衔接。在原材料采购阶段,系统对供应商进行严格筛选与评估,建立
- 安卓系统:在竞争中砥砺前行,铸就辉煌
android
在全球移动操作系统的激烈竞争中,安卓系统一路披荆斩棘,砥砺前行,铸就了今日的辉煌。与苹果的iOS系统相比,安卓最大的优势在于其开放性与兼容性。iOS系统相对封闭,仅适用于苹果自家设备,而安卓系统面向全球开发者与硬件制造商开放,这使得安卓设备在市场上呈现出百花齐放的态势。从高端旗舰到中低端入门机,从知名大品牌到小众新兴品牌,消费者有着丰富多样的选择。这种开放性不仅促进了市场竞争,降低了消费者购买成本
- 云电脑能搭建游戏吗,云电脑能搭建游戏吗,个人云电脑是什么以及怎么连接
后端
远程连接在汽车制造行业助力了远程研发和质量监控。汽车工程师可以通过远程连接共同进行汽车的设计和研发,分享技术方案和实验数据。同时,汽车制造商可以通过远程连接对生产线上的汽车进行质量监控,及时发现并解决问题。远程连接为汽车制造行业的发展提供了技术支持。接下来和大家一起探索云电脑能搭建游戏吗。云电脑能搭建游戏吗:云电脑是可以搭建游戏的。因为云电脑本质上就是一台远程的电脑,只要硬件性能足够,安装好相应的
- PCB 过孔尺寸和焊盘尺寸指南
David WangYang
硬件工程
PCB设计和布局的一些方面看似简单,但答案却很复杂,与制造的许多重要方面有关。这些设计方面之一是PCB过孔尺寸和焊盘尺寸之间的匹配。显然,这两点是相关的;所有PCB过孔都有(或应该有)一个着陆焊盘,用于支撑过孔并提供将走线路由到过孔焊盘的位置。但是,在匹配焊盘和过孔尺寸时,需要遵循一些重要的尺寸指导原则,这种匹配是DFM和可靠性的重要元素。您为设计选择的焊盘尺寸与制造过程中发现的另一个重要设计方面
- CX8903:Ebike自行车仪表电源方案开发,Ebike智能仪表电源芯片
诚芯微科技
社交电子
CX8903:电动Ebike自行车仪表电源方案开发,Ebike智能仪表电源芯片推荐。电动助力自行车EBIKE凭借其环保、健康、低噪、和便捷等特点,成为了越来越受欢迎的骑行便利交通工具。提供电动Ebike自行车仪表电源方案开发、E-BIKE电动助力自行车仪表供电电源解决方案。CX8903采用100V高压制造工艺(芯片最高耐压可到100V以上),SOP-8L贴片封装,CX8903内置100V/90mΩ
- 希望和悲伤都是照亮我们人生的一缕光
山月映雪
我开始并不想读《云边有个小卖部》,但看到好几个学生就都在读这本书,为了了解学生的阅读实际,我就拿起这本书翻看起来。读了十几页,发现小说的语言中不时有一些粗俗的字眼,感觉自己读不下去了。小说一开始把云边镇风景写的特别的美好,我错判为脱离现实的鸳鸯蝴蝶派小说,对于人为制造的童话世界的人与物,我真的不太感兴趣,所以就没有再读了。有天在教室闲转,顺手又拿起了这本书看了起来,这次我才真的看进去了。这部小说除
- 《度五行》生活报报甲午62:不通痛苦,太通也痛苦,要健康快乐,需要通体舒畅。
YangduSam2021
220809壬寅戊申甲午,《度.生活五行》:天干土克水,水生木,木克土。地支寅申冲,寅午合。20220809,周二,兴大上海六班2512天,西交大2013上海班3212天,后TA15332天,度生活619天,今天拜访了一家有趣且当红产业的新创公司AK。AK一开始从事深海新能源储存与供电设备的研发生产制造,2年前开始做移动与家庭储能设备的研发生产制造。觉得有趣是因为这是笔者认知里用科技做降维打击的公
- 2025第十二届广州国际汽车零部件加工技术及汽车模具展览会
ws201907
人工智能大数据汽车
2025第十二届广州国际汽车零部件加工技术及汽车模具展览会时间:2025年11月20日-22日地点:广州保利世贸博览馆(PWTCExpo)预计20000平方米展出面积;400多家参展商:20000多名观众;汇集了各种汽车零部件成品、汽车模具以及机床加工技术的行业盛会;聚集超过80家汽车主机厂以及3000家一二级零部件制造商参观展览会!展会简介:2025第十二届广州国际汽车零部件加工技术及汽车模具展
- 助力新能源汽车产业发展,2025第五届广州国际新能源汽车产业智能制造技术展览会将于11月在广州召开
ws201907
制造汽车
助力新能源汽车产业发展,2025第五届广州国际新能源汽车产业智能制造技术展览会将于11月在广州召开伴随着全球新一轮科技革命和产业变革,汽车与能源、半导体、物联网等领域有关技术加速融合,新能源汽车已成为全球汽车产业转型升级的主要方向。近年来,在相关政策的影响下,新能源汽车市场呈现出快速增长的态势,市场规模不断扩大。截至2020年,中国新能源汽车保有量已超过500万辆,成为全球最大的新能源汽车市场。随
- 2020年 12月3日 渥太华 阴
一生守望一人
今天结课了。全面备战,准备期末考试了。最近看到纽约州立阿尔伯尼法学院和西奈山医学院有一个联合生命科学的硕士学位,有点心动,打算考完试以后找教授和相关负责人问一下。新闻方面,中国第一次实现了外太空运载器发射,嫦娥今天正式启程返家了。这也预示着我们面对载人登月又踏出了自己坚实的一步。同时,我们继美国之后在同一年制造出了量子计算机“九章”。“九章”量子计算机可以以200秒的速度计算出当前最强大超级计算机
- 0416-无题37
傻猪唛的天空之城
办公室外,哗啦啦的下着雨。经过上周闷热,原以为没有春雨了,只是来得晚。天气预报说:本周都是阴雨天气。也好,春天就该是百花盛开,绵绵细雨。刚开始打开编辑器时想发一篇用心写的文章,后来又放弃了。想想有里程碑的意义等过几天再发。日更写得无主题无重点但在末尾我还是用心写了一句鸡汤的啊!给平凡的生活添一点仪式感,自己给自己制造小惊喜。
- 未来软件市场是怎么样的?做开发的生存空间如何?
cesske
软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的?做开发的生存空间如何?一、未来软件市场的发展趋势技术趋势:人工智能与机器学习:随着技术的不断成熟,人工智能将在更多领域得到应用,如智能客服、自动驾驶、智能制造等,这将极大地推动软件市场的增长。云计算与大数据:云计算服务将继续普及,大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率,并
- 《对生命说是》读书笔记2021-5-27
Diana_58d9
静心技巧——换个视角看待问题。尝试一下这个实验,1坐在椅子上,允许自己全身心的沉浸在你最爱的问题当中,你知道头脑热爱咀嚼他们,记录当你被卷入问题时的感受。2站起来有意识地离开那张椅子,想象你现在离开了你的问题。缓缓的围绕椅子走一圈,从不同的角度看看你的问题。在房间中找一个远离问题的空间,开始仔细深入的看看这个问题,他是真实的还是你制造出来的,同样的状况对于其他人来说会是问题吗?3反复体会作战问题里
- 为了那一个约定
王书朋
我和我的学生说好了,不管遇到什么,都要一起努力,这是我们刚遇见时留下的记忆,到现在刚好一年过去。在本周一,我做了一个简单的询问,想看一看经过一个漫长的假期,还有几个人记得努力,所以我一个人一个人的问下去。我所问的内容,就是你有没有记日记和进行课外阅读,两个班将近一百名学生,在我没有要求的情况下。主要是上个学期我们遇到了特殊情况,还没来得及做出要求,就已经进入了假期,因此阴差阳错,为我制造了检验学生
- 世界十大名牌皮鞋都适合什么性格的人?
我信了你滴鞋
前面介绍了《世界公认的五大名鞋,穿过三个以上都是不一般的人》,大概讲了5大名鞋品牌的故事,受到广大读者的关注和讨论,因此在原来的基础上重新整理了世界十大知名皮鞋品牌及特点,揭开他们神秘的面纱,看看到底是哪些人在穿这些鞋子?他们为什么能被公认为是世界排名靠前的品牌?能进入十大名皮鞋的,制造的手工工艺已相近,不同的是品牌设计理念与鞋材选用。正因为每个品牌不同的设计理念,制造出不一样的美丽的产品,适合不
- Day9:别沦为自动化的奴隶——为自己建一座“喷泉广场”
钱塘风华
电子设备解决了小麻烦,却制造了大麻烦。【书名】:混乱——如何成为失控时代的掌控者【作者】:蒂姆哈福德【本书总页码】:288【已读页码】:220(第七章:自动化end)2009年5月31日晚,法航447号航班在电传操作系统失效的情况下,飞行员因习惯了对电传操作系统的依赖,无法对当时的情况作出正确判断,因而也无法作出对应操作——当时的情况:飞机因为急速上升后,过于稀薄的空气密度导致飞机失速,机头抬升,
- 《京瓷哲学》关于开展日常工作读后感
平粤奇妙广东海岛and长隆
至此,又到了《京瓷哲学》这本书的尾声。读书历程,就像在感受一位父母,或者老师,或者是长辈的唠叨和教诲,长篇大论,孜是觉得这些人生的道理谁都会说道两句,当然这种想法很快被印证是错的,没有一颗博爱的心,无私的心,稻盛先生的理念甚至盛和塾可能将不存在。依旧是选择2点分享,第一点制造完美无瑕的产品。随着社会不断的前进发展,人们的标准不再停留于单纯拥有这个层面,而是想拥有更好的。小到日常用餐的摆盘,大到将房
- mysql 隐秘后门_【技术分享】CVE-2016-5483:利用mysqldump备份可生成后门
Toby Dai
mysql隐秘后门
预估稿费:100RMB投稿方式:发送邮件至linwei#360.cn,或登陆网页版在线投稿前言mysqldump是用来创建MySQL数据库逻辑备份的一个常用工具。它在默认配置下可以生成一个.sql文件,其中包含创建/删除表和插入数据等。在导入转储文件的时候,攻击者可以通过制造恶意表名来实现任意SQL语句查询和shell命令执行的目的。另一个与之相关的漏洞利用场景可以参考。攻击场景攻击者已经能够访问
- 解读Servlet原理篇二---GenericServlet与HttpServlet
周凡杨
javaHttpServlet源理GenericService源码
在上一篇《解读Servlet原理篇一》中提到,要实现javax.servlet.Servlet接口(即写自己的Servlet应用),你可以写一个继承自javax.servlet.GenericServletr的generic Servlet ,也可以写一个继承自java.servlet.http.HttpServlet的HTTP Servlet(这就是为什么我们自定义的Servlet通常是exte
- MySQL性能优化
bijian1013
数据库mysql
性能优化是通过某些有效的方法来提高MySQL的运行速度,减少占用的磁盘空间。性能优化包含很多方面,例如优化查询速度,优化更新速度和优化MySQL服务器等。本文介绍方法的主要有:
a.优化查询
b.优化数据库结构
- ThreadPool定时重试
dai_lm
javaThreadPoolthreadtimertimertask
项目需要当某事件触发时,执行http请求任务,失败时需要有重试机制,并根据失败次数的增加,重试间隔也相应增加,任务可能并发。
由于是耗时任务,首先考虑的就是用线程来实现,并且为了节约资源,因而选择线程池。
为了解决不定间隔的重试,选择Timer和TimerTask来完成
package threadpool;
public class ThreadPoolTest {
- Oracle 查看数据库的连接情况
周凡杨
sqloracle 连接
首先要说的是,不同版本数据库提供的系统表会有不同,你可以根据数据字典查看该版本数据库所提供的表。
select * from dict where table_name like '%SESSION%';
就可以查出一些表,然后根据这些表就可以获得会话信息
select sid,serial#,status,username,schemaname,osuser,terminal,ma
- 类的继承
朱辉辉33
java
类的继承可以提高代码的重用行,减少冗余代码;还能提高代码的扩展性。Java继承的关键字是extends
格式:public class 类名(子类)extends 类名(父类){ }
子类可以继承到父类所有的属性和普通方法,但不能继承构造方法。且子类可以直接使用父类的public和
protected属性,但要使用private属性仍需通过调用。
子类的方法可以重写,但必须和父类的返回值类
- android 悬浮窗特效
肆无忌惮_
android
最近在开发项目的时候需要做一个悬浮层的动画,类似于支付宝掉钱动画。但是区别在于,需求是浮出一个窗口,之后边缩放边位移至屏幕右下角标签处。效果图如下:
一开始考虑用自定义View来做。后来发现开线程让其移动很卡,ListView+动画也没法精确定位到目标点。
后来想利用Dialog的dismiss动画来完成。
自定义一个Dialog后,在styl
- hadoop伪分布式搭建
林鹤霄
hadoop
要修改4个文件 1: vim hadoop-env.sh 第九行 2: vim core-site.xml <configuration> &n
- gdb调试命令
aigo
gdb
原文:http://blog.csdn.net/hanchaoman/article/details/5517362
一、GDB常用命令简介
r run 运行.程序还没有运行前使用 c cuntinue
- Socket编程的HelloWorld实例
alleni123
socket
public class Client
{
public static void main(String[] args)
{
Client c=new Client();
c.receiveMessage();
}
public void receiveMessage(){
Socket s=null;
BufferedRea
- 线程同步和异步
百合不是茶
线程同步异步
多线程和同步 : 如进程、线程同步,可理解为进程或线程A和B一块配合,A执行到一定程度时要依靠B的某个结果,于是停下来,示意B运行;B依言执行,再将结果给A;A再继续操作。 所谓同步,就是在发出一个功能调用时,在没有得到结果之前,该调用就不返回,同时其它线程也不能调用这个方法
多线程和异步:多线程可以做不同的事情,涉及到线程通知
&
- JSP中文乱码分析
bijian1013
javajsp中文乱码
在JSP的开发过程中,经常出现中文乱码的问题。
首先了解一下Java中文问题的由来:
Java的内核和class文件是基于unicode的,这使Java程序具有良好的跨平台性,但也带来了一些中文乱码问题的麻烦。原因主要有两方面,
- js实现页面跳转重定向的几种方式
bijian1013
JavaScript重定向
js实现页面跳转重定向有如下几种方式:
一.window.location.href
<script language="javascript"type="text/javascript">
window.location.href="http://www.baidu.c
- 【Struts2三】Struts2 Action转发类型
bit1129
struts2
在【Struts2一】 Struts Hello World http://bit1129.iteye.com/blog/2109365中配置了一个简单的Action,配置如下
<!DOCTYPE struts PUBLIC
"-//Apache Software Foundation//DTD Struts Configurat
- 【HBase十一】Java API操作HBase
bit1129
hbase
Admin类的主要方法注释:
1. 创建表
/**
* Creates a new table. Synchronous operation.
*
* @param desc table descriptor for table
* @throws IllegalArgumentException if the table name is res
- nginx gzip
ronin47
nginx gzip
Nginx GZip 压缩
Nginx GZip 模块文档详见:http://wiki.nginx.org/HttpGzipModule
常用配置片段如下:
gzip on; gzip_comp_level 2; # 压缩比例,比例越大,压缩时间越长。默认是1 gzip_types text/css text/javascript; # 哪些文件可以被压缩 gzip_disable &q
- java-7.微软亚院之编程判断俩个链表是否相交 给出俩个单向链表的头指针,比如 h1 , h2 ,判断这俩个链表是否相交
bylijinnan
java
public class LinkListTest {
/**
* we deal with two main missions:
*
* A.
* 1.we create two joined-List(both have no loop)
* 2.whether list1 and list2 join
* 3.print the join
- Spring源码学习-JdbcTemplate batchUpdate批量操作
bylijinnan
javaspring
Spring JdbcTemplate的batch操作最后还是利用了JDBC提供的方法,Spring只是做了一下改造和封装
JDBC的batch操作:
String sql = "INSERT INTO CUSTOMER " +
"(CUST_ID, NAME, AGE) VALUES (?, ?, ?)";
- [JWFD开源工作流]大规模拓扑矩阵存储结构最新进展
comsci
工作流
生成和创建类已经完成,构造一个100万个元素的矩阵模型,存储空间只有11M大,请大家参考我在博客园上面的文档"构造下一代工作流存储结构的尝试",更加相信的设计和代码将陆续推出.........
竞争对手的能力也很强.......,我相信..你们一定能够先于我们推出大规模拓扑扫描和分析系统的....
- base64编码和url编码
cuityang
base64url
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.io.StringWriter;
import java.io.UnsupportedEncodingException;
- web应用集群Session保持
dalan_123
session
关于使用 memcached 或redis 存储 session ,以及使用 terracotta 服务器共享。建议使用 redis,不仅仅因为它可以将缓存的内容持久化,还因为它支持的单个对象比较大,而且数据类型丰富,不只是缓存 session,还可以做其他用途,一举几得啊。1、使用 filter 方法存储这种方法比较推荐,因为它的服务器使用范围比较多,不仅限于tomcat ,而且实现的原理比较简
- Yii 框架里数据库操作详解-[增加、查询、更新、删除的方法 'AR模式']
dcj3sjt126com
数据库
public function getMinLimit () { $sql = "..."; $result = yii::app()->db->createCo
- solr StatsComponent(聚合统计)
eksliang
solr聚合查询solr stats
StatsComponent
转载请出自出处:http://eksliang.iteye.com/blog/2169134
http://eksliang.iteye.com/ 一、概述
Solr可以利用StatsComponent 实现数据库的聚合统计查询,也就是min、max、avg、count、sum的功能
二、参数
- 百度一道面试题
greemranqq
位运算百度面试寻找奇数算法bitmap 算法
那天看朋友提了一个百度面试的题目:怎么找出{1,1,2,3,3,4,4,4,5,5,5,5} 找出出现次数为奇数的数字.
我这里复制的是原话,当然顺序是不一定的,很多拿到题目第一反应就是用map,当然可以解决,但是效率不高。
还有人觉得应该用算法xxx,我是没想到用啥算法好...!
还有觉得应该先排序...
还有觉
- Spring之在开发中使用SpringJDBC
ihuning
spring
在实际开发中使用SpringJDBC有两种方式:
1. 在Dao中添加属性JdbcTemplate并用Spring注入;
JdbcTemplate类被设计成为线程安全的,所以可以在IOC 容器中声明它的单个实例,并将这个实例注入到所有的 DAO 实例中。JdbcTemplate也利用了Java 1.5 的特定(自动装箱,泛型,可变长度
- JSON API 1.0 核心开发者自述 | 你所不知道的那些技术细节
justjavac
json
2013年5月,Yehuda Katz 完成了JSON API(英文,中文) 技术规范的初稿。事情就发生在 RailsConf 之后,在那次会议上他和 Steve Klabnik 就 JSON 雏形的技术细节相聊甚欢。在沟通单一 Rails 服务器库—— ActiveModel::Serializers 和单一 JavaScript 客户端库——&
- 网站项目建设流程概述
macroli
工作
一.概念
网站项目管理就是根据特定的规范、在预算范围内、按时完成的网站开发任务。
二.需求分析
项目立项
我们接到客户的业务咨询,经过双方不断的接洽和了解,并通过基本的可行性讨论够,初步达成制作协议,这时就需要将项目立项。较好的做法是成立一个专门的项目小组,小组成员包括:项目经理,网页设计,程序员,测试员,编辑/文档等必须人员。项目实行项目经理制。
客户的需求说明书
第一步是需
- AngularJs 三目运算 表达式判断
qiaolevip
每天进步一点点学习永无止境众观千象AngularJS
事件回顾:由于需要修改同一个模板,里面包含2个不同的内容,第一个里面使用的时间差和第二个里面名称不一样,其他过滤器,内容都大同小异。希望杜绝If这样比较傻的来判断if-show or not,继续追究其源码。
var b = "{{",
a = "}}";
this.startSymbol = function(a) {
- Spark算子:统计RDD分区中的元素及数量
superlxw1234
sparkspark算子Spark RDD分区元素
关键字:Spark算子、Spark RDD分区、Spark RDD分区元素数量
Spark RDD是被分区的,在生成RDD时候,一般可以指定分区的数量,如果不指定分区数量,当RDD从集合创建时候,则默认为该程序所分配到的资源的CPU核数,如果是从HDFS文件创建,默认为文件的Block数。
可以利用RDD的mapPartitionsWithInd
- Spring 3.2.x将于2016年12月31日停止支持
wiselyman
Spring 3
Spring 团队公布在2016年12月31日停止对Spring Framework 3.2.x(包含tomcat 6.x)的支持。在此之前spring团队将持续发布3.2.x的维护版本。
请大家及时准备及时升级到Spring
- fis纯前端解决方案fis-pure
zccst
JavaScript
作者:zccst
FIS通过插件扩展可以完美的支持模块化的前端开发方案,我们通过FIS的二次封装能力,封装了一个功能完备的纯前端模块化方案pure。
1,fis-pure的安装
$ fis install -g fis-pure
$ pure -v
0.1.4
2,下载demo到本地
git clone https://github.com/hefangshi/f