二叉树介绍

二叉树介绍

tonim

 介绍

     在这篇文章中，我介绍了二叉树和层级数据结构。在样例工程中，我比较了二叉树和快速排序。二叉树是用C++模板定义的。它可以用于支持C++的任何环境和支持比较运算符（< 和>）的任何类型的数据。描述简单易懂。为了使用模板你需要在你的工程中包含BTreen.h。为了平衡和优化数据插入，我使用了一个简单的重排序算法来替代Red-Black和AVL树。其有点是数据插入和树的创建所需时间跟少。甚至，如果不是完全平衡，这个方法保证数据查询需要log2比较操作。

     我主要关心的是多维数据结构因此我用了对于N维易通用化的算法。

背景

     二叉树是层级式数据结构，它允许以一维数据形式插入和快速最近邻查找。它可以被用于替代快速排序和二分查找来快速找到一个数组中的最近点。二叉树有结构简单的优点，这允许它对多维数据能够通用化。--所谓的KD树。因此，理解它是怎样工作，怎样执行数据搜索是很有用的。我将尽使得解释简单易懂。

     首先，让我们来定义一颗树。一棵树是有一个节点集构成的数据结构。每一个节点都链接其他的一些节点，即所谓的父节点和子节点。它们之间的不同是子节点是按照某种规则选择的而父节点链节只是我们怎样访问过一个给定的节点的历史。

二叉树有两个子树——左子树和右子树以及一个父节点。对于最近邻查找和树的优化父节链结必要的。

        树的每一个节点包含值为X的某种类型的数据。左子节点的X值必须比相对应的的右节点的值要小——X>Left-X并且Right-X>X。这是二叉树的基本准则。树也必须有一个根节点Root。根节点是唯一个没有父节点的节点。但一个值为X的新节点加入到树中的时候，我们总是从根节点开始向下行直到找到一个空位。每次当我们经过一个节点时，我们通过比教值X和这个节点的值的大小来决定是向左还是向右，如果X较小，则向左，如果较大则向右。

     在上面的例子中，新的值是100。为了找到这个值的位置，在树中一步一步的走。从根节点开始我们检查100是大于还是小于127。在这个例子中它小于，因此我们转向左侧值位111的节点。现在，100小于111那么我们向左转向值为60的节点。这次100大于60，但是60没有右子节点，那是在一个空位，因此我们将100放在这。

      现在让我们看看二叉树的有用之处。然我们看看限定范围和最近邻是怎样被找到的。选择一个新的值125作为例子。在两个存在的树的值之间，我们需要确定那个是125。我们再次从父节点127开始，经过几步我们就到达了节点115:

      现在很明显，既然125是115的右子节点，125距离最左邻居最近。但是查找右侧的值确不是如此简单。在这个例子中，树的根节点是127。二叉树的规则是限定的值是具有比125大的值的第一个父节点。因此我们不得不在树中上行直到我们找到值比125大的一个父节点。在某些情况下节点只有一个限定的邻居是可能的。二叉树声明、数据插入和最近邻的代码将在下面给出。

代码

     二叉树的声明和实现都在BTree.h中。BTNode类包含插入和删除函数。模板类型位X，有两个指针指向左子节点和有子节点，一个指针指向父节点。我对标准二叉树作了两个小的扩展，增加了一个布尔型成员变量——ParentOrientation和一个用来优化的成员函数moveup（）。

//Binary Tree Node
template <class>
class BTNode
{
public:
    BTNode();
    BTNode(Xtype x);
    bool Delete_Tree(BTNode<xtype>* Root);
    BTNode(BTNode<xtype>* k1, BTNode<xtype>* k2);
    BTNode<xtype> *Left, *Right, *Parent;
    BTNode<xtype>* place(BTNode<xtype>* T);
    BTNode<xtype>* insert(Xtype x,bool&root_changed,bool optimize=true);
    bool insert(BTNode<xtype>* node,bool&root_changed,bool optimize=true);
    void remove();
    int count_childs();
    bool  moveup();
    Xtype x;
    bool ParentOrientation ; //where is child WRT parent ? 0=left 1=right
};

     ParentOrientation成员用来插入和最近邻搜索的优化。它用来根据父节点来标识一个子节点的方向；如果它是0，那么转向其左侧子节点，如果是1则转向右侧。当然，我们能够通过比较子节点和父节点的值来决定方向，但是因为比较运算符< 和 > 运算速度可能比较慢，所有我们使用这个标帜来减少它们的使用。成员函数moveup()用来在树中向上移动节点。它改善了树的平衡，优化了插入操作。插入操作如下：

//insert node to the tree, starts from current node
template <class>
bool
BTNode<xtype>::insert(BTNode<xtype>* node,bool&root_changed, bool optimize)
{
    BTNode<xtype>* pNext = this;
    BTNode<xtype>* pFather;
    while(pNext) //do not insert if already exist
    {
        pFather = pNext;
        if(node->x < pNext->x)
            pNext = pNext->Left;
        else if(node->x > pNext->x)
            pNext = pNext->Right;
        else
            return false;
    }

    if(!pNext) //empty place, do not insert value twice
    {
        node->Parent = pFather;
        if(node->x < pFather->x)
        {
            pFather->Left = node;
            node->ParentOrientation = 0 ;
        }
        else
        {
            pFather->Right = node;
            node->ParentOrientation = 1;
        }

        if(optimize)
            root_changed = node->moveup();
        else
            root_changed = false ;

        return true;
    }
    return false;
}

 前面解释了最近邻搜索，下面是代码:

/*   nearest neighbours search
   input:
    Root - the root of the tree
    x - template type with search target value

   output:
    l - the left limiting value or INVALID_VALUE if there
is no neighbour to left
    r - the right limiting value or INVALID_VALUE if there
is no neighbour to right
   
   returns: 
      - the closest value to x
      - INVALID_VALUE - empty tree
*/
template <class>
Xtype FindNearest(BTNode<xtype>* Root, Xtype x, Xtype* l, Xtype* r)
{
    Xtype left,right;
    BTNode<xtype>* pNext = Root;
    BTNode<xtype>* pFather;
    bool ParentOrientation ;
    while(pNext)
    {
        pFather = pNext;
        if(x<pnext->x)
        {
            pNext = pNext->Left;
            ParentOrientation = false;
        }
        else if(x>pNext->x)
        {
            pNext = pNext->Right;
            ParentOrientation = true;
        }
        else
        {
            *l = pNext->x;
            *r = pNext->x;
            return pNext->x;
        }
    }

    if(!ParentOrientation)  //x < pFather->x
    {
        right = pFather->x;
        //go up in the tree    and search for the left limit
        ParentOrientation = pFather->ParentOrientation ;
        pFather = pFather->Parent;
        while(pFather && !ParentOrientation)
    {
           //search parent to the left
            ParentOrientation = pFather->ParentOrientation ;
            pFather = pFather->Parent;
        }

        if(!pFather)
        {
            *l = INVALID_VALUE;  //no neighbour to the left
            *r = right;
            return right;
        }
        else
        {
            *l = pFather->x;
            *r = right;
            return (x-pFather->x < right-x ? pFather->x:right);
        }
    }

    else //x > pFather->x
    {
        left = pFather->x;
        // go up in the tree and search for the right limit       
        ParentOrientation = pFather->ParentOrientation ;
        pFather = pFather->Parent;
        while(pFather && ParentOrientation)
    {
           //search parent to the right
            ParentOrientation = pFather->ParentOrientation ;
            pFather = pFather->Parent;
        }

        if(!pFather)
        {
            *l = left; 
            *r = INVALID_VALUE;   //no neighbour to the right
            return left;
        }
        else
        {
            *l = left;
            *r = pFather->x;
            return (x-left < pFather->x-x ? left:pFather->x);;
        }
    }

    return INVALID_VALUE; //empty tree
}

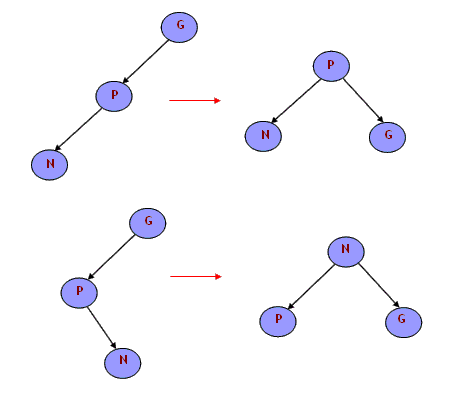
    就像上面提到的，树的优化是用moveup（）循环调用来实现的。为什么需要优化呢？好，如果在二叉树中包含的值都是以随机的（无序的）顺序到来，那么这棵树自然是平衡的。但是没有谁能够保证这些值不是以非随机的模式到了。例如，如果就像2，5，8，11...这样，那么二叉树将变成了链表，最近邻搜索将变成顺序查找，这是无效率的。有许多平衡的方法——Red-Black、AVL...我更喜欢我直接的本地树优化，它排除了最坏情况。下面举例说明它是怎样工作的：

        这里N是被插入的节点，P是它的父节点，G是它的祖父节点。如果像上图左侧两种情况或它们的镜像情况，向上移动P或N，向下移动G是可行的。三个节点-N、P和G重新排序成右侧那样。这样，树的高度减少了，最坏的情况被校正了并且改善了树的平衡。从我执行的测试可以发现插入操作和树的操作减慢了不到10%。如果你增加随机选择的数据的平均高度，那么你会发现效率仍然是慢10%，但是这个比率会随着数据量的增长而增加，保证平均高度总是log₂N，这里N是数据量。这意味着当我们在一个大数组中（100 000）寻找一个值时经过的平均路径大约是20，因为2的20是次幂是100 000。工程的源代码包含了执行这些测试的应用程序。如果你想要检查不同水平的平均树的高度，修改POINTS_NUM的值，修改generate_random_point()循环次数如果太大的话。

原文