[置顶] [数字图像处理]灰度变换——直方图处理
直方图均衡
一副图像的直方图,表示了其灰度分布的特性。对于数字图像来说,假设灰度值k出现了![]() 次,那么其概率密度函数如下所示。
次,那么其概率密度函数如下所示。
这个式子,表示了像素的灰度值为k概率。其中,M与N为图像的尺寸。
对于一幅动态范围较窄的图像,其归一化灰度直方图如下所示。
对于此类图像,使用灰度拉伸,也能使其的动态范围得到改善,增强图像对比度。但是,灰度拉伸从本质上来讲,是很暧昧的,灰度拉伸没有什么明确的目的,只是依靠某个函数的做了灰度变换,使得图像的在灰度直方图的分布范围扩大。灰度拉伸对于结果没有严格的要求,因此根据变换函数的不同,灰度拉伸有无数种结果。
与灰度拉伸不同的是,直方图均衡的目的就比较明确,使用某个特殊的函数,使原图像的灰度分布平均化。为了将其平均化,这里需要用到累积分布函数(Probability Density Function)的概念。
所谓的平均化,直方图均衡的目的是将一幅图的累积分布的曲线(下图左),变为下图右的分布形式。
(左)原图的累积分布曲线 (右)理想化直方图均衡后的累积分布曲线
从右图中可以看出,为了保证直方图均衡后的累积分布曲线是一条倾角为45°的直线,那么,变换后的函数的概率密度函数应与输入值无关,且保持一个常量。输入r与输出s有如下关系,
将变换关系
带入上式子,可得
将其带入输入r与输出s关系,可得到
到此,已经可以看出,输出的概率密度函数,与s的取值无关。很明显,这个分布是绝对平均的。
但是,事实上,上面的式子均是在连续的情况下的。在数字图像的领域,我们必须将其离散化,才能使用。离散的情况下,其累计分布函数如下所示。
至此,直方图均衡就完成了。
为了验证结果,其直方图均衡后的图像与灰度直方图如下所示。
结果就是这样了。但是,呃!!!!问题来了,这是直方图均衡么?这跟灰度拉升有何区别,而且其均衡后的图像的直方图也不是一个很平均的值,和我们的构想有很大区别。这个结果真的没问么?为了回答这个问题,将其原图像的累积分布函数与直方均衡后的累积分布函数画出来,如下。
(左)原图的累积分布曲线 (右)直方图均衡后的累积分布曲线
从累积分布曲线中,我们可以看到,直方图均衡后的曲线,确实跟我们设想的理想曲线很接近!由于我们证明的时候,是在连续的情况下去思考的,所以,将其离散之后,多少是有不理想的情况发生的。均衡后的累积分布曲线确实是一个不错的结果。这样看来,我们才能看清楚直方图均衡的本质。若不是这样,还真不知道直方均衡与灰度拉伸的区别。
为此,直方图均衡成功,Matlab代码如下。
直方图匹配
前面,我们说了直方图的均衡,直方均衡可以得到一个灰度直方图分布平均的图像。但是有一些问题,直方图均衡的结果是唯一的。这是其优点,也是其缺点。优点在于,无需多余的参数,就可以实现对比度的增强。缺点在于,没有参数,对于结果无法调整。举个栗子(输入法君卖萌了╭(╯3╰)╮),一幅很黑的图像,使用直方图均衡的话,这幅图像的直方均衡结果,将使得图像偏白。使用 《Digital Image Processing》 Rafael C. Gonzalez / Richard E. Woods 的例子来说,看下图。如上图所示,直方均衡的结果不是很理想。由直方均衡的结果看来,我们能看到,其实对比原图,原图一些细节已经显露出来了,只要稍加修改,就可以得到很理想的增强结果。为此,直觉告诉我们(不要吐槽这句话,有时候直觉就是那么简单。\(≧▽≦)/),只需要将原图的灰度直方图稍微左移一些即可。但是,直方均衡却是不可调整的,为此,就有了直方图匹配。
对于原图像,其概率分布函数是
其输出也就是直方均衡的结果。为了实现直方图匹配,我们还需要一个函数,也就是我们所期待的概率分布函数。这个概率分布函数的概率分布函数如下所示。
其中,z代表了期望的分布。我们假设如下关系成立。
也就是,我们所期待的直方图分布的概率分布函数与原图像的直方图概率分布函数相等。那么,我们可以利用G()的反函数,我们也就可以得到我们所期待的直方图。
上面的描述可能太过拖沓,我们采用简洁一点的描述。
一. 将原图进行直方图均衡。
二. 假设我们期待的分布,直方均衡的结果与原图直方图均衡的结果一致。利用反函数,还原成我们期待的分布。
所实现的直方图均衡结果如下所示。
根据直方图匹配的结果,我们可以看出,所得出的结果和我们所期待的分布很接近。其结果也和我们的初衷一样,使得原图的直方图稍微左移了一些。所得到的结果比起直方均衡要好得多。
其Matlab代码如下。
博客地址:http://blog.csdn.net/thnh169/
![[置顶] [数字图像处理]灰度变换——直方图处理_第1张图片](http://img.e-com-net.com/image/info5/0c882adcd3ee4c4babdf953bad0143bc.jpg)
![[置顶] [数字图像处理]灰度变换——直方图处理_第2张图片](http://img.e-com-net.com/image/info5/62d9bb3e69ad450196b093057e34ff6b.jpg)

![[置顶] [数字图像处理]灰度变换——直方图处理_第3张图片](http://img.e-com-net.com/image/info5/eca998aacbb04c9f91eaf8418156bebf.jpg)
![[置顶] [数字图像处理]灰度变换——直方图处理_第4张图片](http://img.e-com-net.com/image/info5/73d1379e1f834314a0505de51a20c63c.jpg)
![[置顶] [数字图像处理]灰度变换——直方图处理_第5张图片](http://img.e-com-net.com/image/info5/e561ded26d644017b0e2d7530a080b28.jpg)
![[置顶] [数字图像处理]灰度变换——直方图处理_第6张图片](http://img.e-com-net.com/image/info5/5d5f17c7f1eb4c98a8a5f725a8bd710a.jpg)
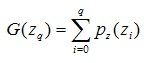
![[置顶] [数字图像处理]灰度变换——直方图处理_第7张图片](http://img.e-com-net.com/image/info5/97711265ea364236b5db2bfa450e984b.jpg)