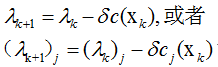最优化之PH解法

之前几篇blog分别讨论了无约束最优性条件，等式约束最优性条件，不等式约束最优性条件。根据最优性条件，我们可以用解析法求解。

还有序列求解的外罚函数法和内罚函数法。

 

小结一下：

无约束问题用微积分的知识，或者简单的下降法可以求解。

等式约束问题，构造拉格朗日乘子，再用解析法求解。

不等式约束问题复杂一点，构造KKT条件（包括拉格朗日乘子，以及相应的约束）求解。

一般情况下，拉格朗日乘子，或者KKT条件无法直接求解。经证明，拉格朗日乘子没有极小值，因此序列迭代求解也不行。

我们引进的外罚函数与内罚函数可以用下降算法解决上述问题，不过其有各自的病态缺陷。

 

有这么一种方法，把罚函数+拉格朗日乘子结合起来求解。这里讨论这种方法。

 

增广拉格朗日函数

先考虑等式约束情况下。 

函数：

称为增广拉格朗日函数。

1.      单独的L函数，没有极小值，无法序列求解。

2.      单独的罚函数病态性质，很难得到最优解。

于是联合两个函数，称为增广拉格朗日函数。

 

通过增广矩阵转化为无约束问题：

根据最优性条件可得：

其中x*是x的稳定点。不过上式中的lambda*未知，yita未知，x未知。三个未知数，如何求解？

 

先解决yita

在单纯的外罚函数，或者内罚函数方法中，我们把yita设定为很大的值，用序列下降法可以逼近得到近似最优解。不过由于yita很大，容易造成病态的函数性质。那么在这种情况下会这样吗？

经证明，在满足一定的条件下，存在一个yita*，对于所有的yita>yita*得到的x，x等于原最优化的最优解x*。于是我们只要取yita大于一定大小。这也就解决了罚函数的病态问题。

 

然后是lambda*

X*是在Lambda*的情况下的最优解，于是在lambda*未知时，无法求得x*;同样，x*未知的情况下，也无法求lambda*。一个简单的方法就是两个变量交叉序列求解。

 

X，lambda的更新

在固定lambda之后，就可以直接用解析法直接解x。假设根据lambda(k)解得的X为x(k),那么有：

又因为，不加yita的拉格朗日乘子，根据KKT条件，如果lambda*和x*是最优解，有：

由此，观察对比两个式子，我们可以如下更新lambda：

这样更新使得其后一项逼近最优解的形式。

 

迭代结束条件

有上可以看出，当lambda收敛，x*满足KT条件时，有：

即为更新的结束条件。

 

加速迭代

实践中发现，迭代的过程往往过慢，我们可以增大yita的放大系数后再迭代。其中收敛速度可用||c(xk)||/||c(xk-1)||来度量。

 

具体解法步骤

等式约束乘子法解法——PH算法

 

如上为等式约束的PH算法。

不等式的情况下，先用辅助变量修改为等式情况，再如上求解即可。

 

Matlab求解

下面用PH算法求解一个简单的问题：

代码：

clear;
clc;
x(1)=0;
x(2)=0;
lambda=1;
yita=100;
c=2;
sita=0.5;
k=1;
e=0.01;
E=1;
while(E>0.01)
    temp_E=(x(1)+x(2)-2);
    x(1)=2*yita+lambda/(2*yita+2);
    x(2)=2*yita+lambda/(2*yita+2);    
    E=(x(1)+x(2)-2);
    if(E<0.01)
        break;
    end
    if(E/temp_E>sita)
        yita=c*yita;
    end
    lambda=lambda-yita*(x(1)+x(2)-2);
end

得到结果：

X1=1.0002;

X2=1.0002;

minY=2.0008;

迭代次数：4