面试准备—后缀数组、伴随数组
1、后缀数组
可参考http://dongxicheng.org/structure/suffix-array/ ,最简单的理解,后缀数组是“排第几的是谁?”,名次数组是“你排第几?”。关于后缀数组生成,参考专门算法。不列。常见笔试题
(1) 可重叠最长重复子串。给定一个字符串,求最长重复子串,这两个子串可以重叠。
『解析』只需要求height 数组里的最大值即可。
(2) 不可重叠最长重复子串。给定一个字符串,求最长重复子串,这两个子串不能重叠。
『解析』先二分答案,把题目变成判定性问题:判断是否存在两个长度为k 的子串是相同的,且不重叠。解决这个问题的关键还是利用height 数组。把排序后的后缀分成若干组,其中每组的后缀之间的height 值都不小于k。例如,字符串为“aabaaaab”,当k=2 时,后缀分成了4 组:
(3) 可重叠的k 次最长重复子串。给定一个字符串,求至少出现k 次的最长重复子串,这k 个子串可以重叠。
『解析』 先二分答案,然后将后缀分成若干组。不同的是,这里要判断的是有没有一个组的后缀个数不小于k。如果有,那么存在k 个相同的子串满足条件,否则不存在。这个做法的时间复杂度为O(nlogn)。
(4) 最长回文子串。给定一个字符串,求最长回文子串。
『解析』 将整个字符串反过来写在原字符串后面,中间用一个特殊的字符隔开。这样就把问题变为了求这个新的字符串的某两个后缀的最长公共前缀。
(5) 连续重复子串。给定一个字符串L,已知这个字符串是由某个字符串S 重复R 次而得到的,求R 的最大值。
『解析』穷举字符串S 的长度k,然后判断是否满足。判断的时候,先看字符串L 的长度能否被k 整除,再看suffix(1)和suffix(k+1)的最长公共前缀是否等于n-k。在询问最长公共前缀的时候,suffix(1)是固定的,所以RMQ问题没有必要做所有的预处理, 只需求出height 数组中的每一个数到height[rank[1]]之间的最小值即可。整个做法的时间复杂度为O(n)。
(6) 重复次数最多的连续重复子串。给定一个字符串,求重复次数最多的连续重复子串。
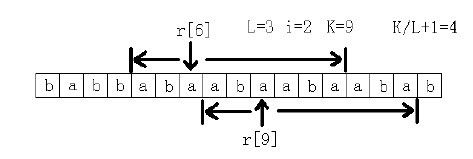
『解析』先穷举长度L,然后求长度为L 的子串最多能连续出现几次。首先连续出现1 次是肯定可以的,所以这里只考虑至少2 次的情况。假设在原字符串中连续出现2 次,记这个子字符串为S,那么S 肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个。所以只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远,记这个总长度为K,那么这里连续出现了K/L+1 次。最后看最大值是多少。
穷举长度L 的时间是n,每次计算的时间是n/L。所以整个做法的时间复杂度是O(n/1+n/2+n/3+……+n/n)=O(nlogn)。
(7) 最长公共子串。给定两个字符串A 和B,求最长公共子串。
『解析』先将第二个字符串写在第一个字符串后面,中间用一个没有出现过的字符隔开,再求这个新的字符串的后缀数组。当suffix(sa[i-1]) 和suffix(sa[i])不是同一个字符串中的两个后缀时,max{height[i]}才是满足条件
(8) 长度不小于k 的公共子串的个数。给定两个字符串A 和B,求长度不小于k 的公共子串的个数(可以相同)。
『解析』基本思路是计算A 的所有后缀和B 的所有后缀之间的最长公共前缀的长度,把最长公共前缀长度不小于k 的部分全部加起来。先将两个字符串连起来,中间用一个没有出现过的字符隔开。按height 值分组后,接下来的工作便是快速的统计每组中后缀之间的最长公共前缀之和。扫描一遍,每遇到一个B 的后缀就统计与前面的A 的后缀能产生多少个长度不小于k 的公共子串,这里A 的后缀需要用一个单调的栈来高效的维护。然后对A 也这样做一次。
百度实习生笔试题,貌似有道
2、伴随数组
其实搜了下伴随数组,参考http://blog.csdn.net/v_JULY_v/article/details/6441279,其他都没这个说法,姑且认为是这么叫吧,就是定义一个辅助存储空间,跟计数排序的数组挺像,在不少地方,求亲合数,求完数,求素数都可以用到
比如,素数的筛选法实现
#include <iostream>
#include <cmath>
using namespace std;
const int MAX = 100000 ;
bool prime[MAX];
void searchPrime()
{
int i=0,j=0;
while (i++ < MAX )
prime[i] = true;
prime[1] = false;
for (i=2; i< sqrt(MAX) ; i ++)
{
if (prime[i])
{
j = i<<1 ; //j=2*i
while (j < MAX)
{
prime[j] = false;
j += i;
}
}
}
}
int main()
{
searchPrime();
int i;
for (i=0 ; i<MAX ; i++)
{
if (prime[i])
cout << i << endl;
}
return 0;
}
亲合数的实现(基本来自http://blog.csdn.net/v_JULY_v/article/details/6441279,定义在其中有)
#include <iostream>
#include <cmath>
using namespace std;
const int N = 50000;
int sum[N] = {0};
int main()
{
int i,j;
for (i = 0; i <= N; i++)
{ //1是所有数的真因数所以全部置1
sum[i] = 1;
}
for (i=2 ; i < N>>1; i++)
{
j = i<<1;
while (j <= N)
{
//将所有i的倍数的位置上加i
sum[j] += i;
j += i;
}
}
for (i = 200; i < N; i++)
{
if (sum[i] > i && sum[i] <= N && sum[sum[i]] == i)
{
cout << i << " " << sum[i] << endl;
}
}
return 0;
}
完数的实现
#include <iostream>
#include <cmath>
using namespace std;
const int N = 50000;
int sum[N] = {0};
int main()
{
int i,j;
for (i = 0; i <= N; i++)
{ //1是所有数的真因数所以全部置1
sum[i] = 1;
}
for (i=2 ; i < N>>1; i++)
{
j = i<<1;
while (j <= N)
{
//将所有i的倍数的位置上加i
sum[j] += i;
j += i;
}
}
for (i = 1; i < N; i++)
{
if (sum[i] == i)
{
cout << i << " " << sum[i] << endl;
}
}
return 0;
}
三段代码都非常相似,定义一个辅助数组,2个是保存因子的和,1个是保存是否是素数的标记,纯粹像计数排序了
没了,先就这样吧