Stanford机器学习---第四讲. 神经网络的表示 Neural Networks representation

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。（https://class.coursera.org/ml/class/index）

第四讲——Neural Networks 神经网络的表示

===============================

（一）、为什么引入神经网络？——Nonlinear hypothesis

（二）、神经元与大脑（Neurons and Brain）

（三）、神经网络的表示形式

（四）、怎样用神经网络实现逻辑表达式？

（五）、分类问题（Classification）

本章主要围绕神经网络的建模及其线性表示（即neural networks的representation）做以初步了解，在下一章中将会有更详细的神经网络如何学习方面的知识。

===============================

（一）、为什么引入神经网络？——Nonlinear hypothesis

之前我们讨论的ML问题中，主要针对Regression做了分析，其中采用梯度下降法进行参数更新。然而其可行性基于假设参数不多，如果参数多起来了怎么办呢？比如下图中这个例子：从100*100个pixels中选出所有XiXj作为logistic regression的一个参数，那么总共就有5*10^7个feature，即x有这么多维。

所以引入了Nonlinear hypothesis，应对高维数据和非线性的hypothesis（如下图所示）：

===============================

（二）、神经元与大脑（neurons and brain）

神经元工作模式：

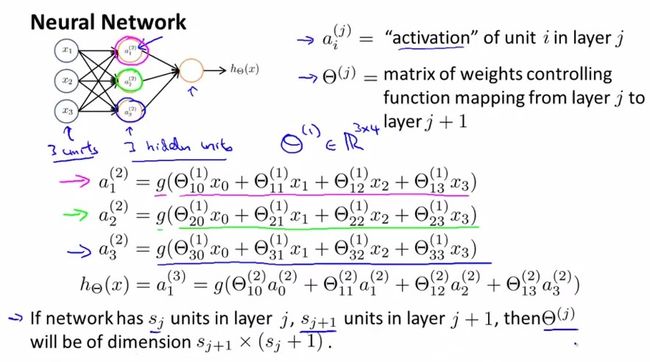
神经网络的逻辑单元：输入向量x（input layer），中间层a(2,i)（hidden layer）, 输出层h(x)（output layer）。

其中，中间层的a(2,i)中的2表示第二个级别（第一个级别是输入层），i表示中间层的第几个元素。或者可以说，a(j,i) is the activation of unit i in layer j.

===============================

（三）、神经网络的表示形式

从图中可知，中间层a(2，j)是输入层线性组合的sigmod值，输出又是中间层线性组合的sigmod值。

下面我们进行神经网络参数计算的向量化：

令z⁽²⁾表示中间层，x表示输入层，则有

，

z⁽²⁾=Θ⁽¹⁾x

a⁽²⁾=g(z⁽²⁾)

或者可以将x表示成a⁽¹⁾，那么对于输入层a⁽¹⁾有[x_0~x_3]4个元素，中间层a⁽²⁾有[a⁽²⁾₀~a⁽²⁾₃]4个元素（其中令a⁽²⁾₀=1），则有

h(x)= a⁽³⁾=g(z⁽³⁾)

z⁽³⁾=Θ⁽²⁾a⁽²⁾

通过以上这种神经元的传递方式（input->activation->output）来计算h(x), 叫做Forward propagation, 向前传递。

这里我们可以发现，其实神经网络就像是logistic regression，只不过我们把logistic regression中的输入向量[x₁~x₃]变成了中间层的[a⁽²⁾₁~a⁽²⁾₃], 即

h(x)=g(Θ⁽²⁾₀ a⁽²⁾₀+Θ⁽²⁾₁ a⁽²⁾₁+Θ⁽²⁾₂ a⁽²⁾₂+Θ⁽²⁾₃ a⁽²⁾₃)

而中间层又由真正的输入向量通过Θ⁽¹⁾学习而来，这里呢，就解放了输入层，换言之输入层可以是original input data的任何线性组合甚至是多项式组合如set x1*x2 as original x1...另外呢，具体怎样利用中间层进行更新下面会更详细地讲；此外，还有一些其他模型，比如：

===============================

（四）、怎样用神经网络实现逻辑表达式？

神经网路中，单层神经元（无中间层）的计算可用来表示逻辑运算，比如逻辑AND、逻辑或OR

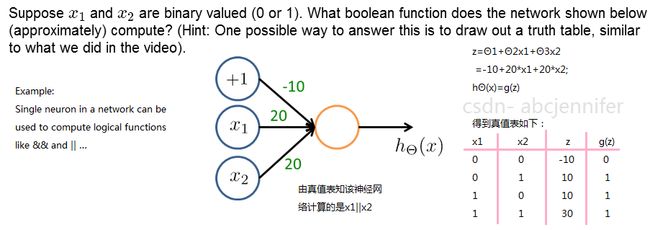
举例说明：逻辑与AND；下图中左半部分是神经网络的设计与output层表达式，右边上部分是sigmod函数，下半部分是真值表。

给定神经网络的权值就可以根据真值表判断该函数的作用。再给出一个逻辑或的例子，如下图所示：

以上两个例子只是单层传递，下面我们再给出一个更复杂的例子，用来实现逻辑表达< x1 XNOR x2 >, 即逻辑同或关系，它由前面几个例子共同实现：

将AND、NOT AND和 OR分别放在下图中输入层和输出层的位置，即可得到x1 XNOR x2，道理显而易见：

a²₁ = x1 && x2

a²₂ = （﹁x1）&&（﹁x2） 

a³₁ =a²₁ ||a²₁ =(x1 && x2) ||  （﹁x1）&&（﹁x2） = x1 XNOR x2；

应用：手写识别系统

===============================

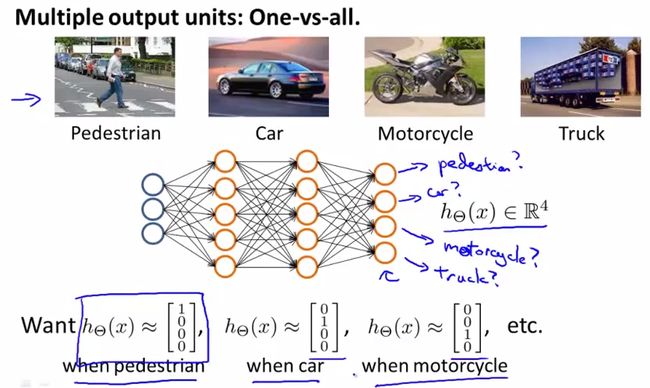
（五）、分类问题（Classification）

记得上一章中我们讲过的one-vs-all分类问题么？one-vs-all方法是把二类分类问题到多类分类的一个推广，在这里，我们就讲述如何用神经网络进行分类。网络设计如下图所示：

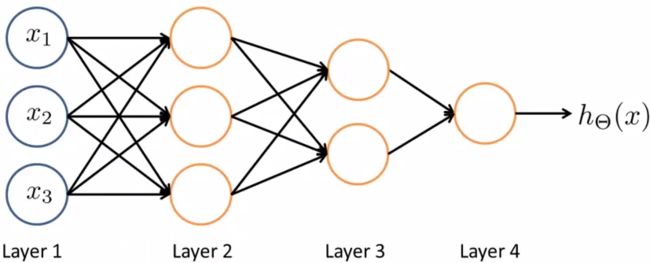
输入向量x有三个维度，两个中间层，输出层4个神经元分别用来表示4类，也就是每一个数据在输出层都会出现[a b c d]^T，且a,b,c,d中仅有一个为1，表示当前类。

===============================

小结

本章引入了ML中神经网络的概念，主要讲述了如何利用神经网络的construction及如何进行逻辑表达function的构造，在下一章中我们将针对神经网络的学习过程进行更详细的讲述。