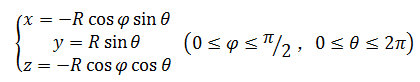WPF 3D model - Sphere, Cone, and Cylinder
Extending Visual3D - Sphere, Cone, and Cylinder
http://blogs.msdn.com/b/danlehen/archive/2005/10/16/481597.aspx
He put together a short sample which derives a Sphere, a Cone, and a Cylinder primitive from ModelVisual3D. (Source available here.)
You will notice that these primitives are directly usable from Xaml:
<Viewport3D Camera=”{Camera}” >
<my:Sphere3D Transform=”{XForm1}” Material=”{Azul}” />
<my:Cone3D Transform=”{XForm2}” Material=”{Tulips}” />
<my:Cylinder3D Transform=”{XForm3}” Material=”{Autumn}” />
</Viewport3D>
Perspective : Easy 3D programming with WPF
http://www.odewit.net/ArticleContent.aspx?id=Wpf3DIntro&lang=en&format=xaml
[Lieo原创]圆柱体的三角形剖分——使用WPF 3D绘制圆柱体
上个学期在做某个软件时需要使用WPF绘制一些基本的三维物体。找了很多资料,发现大多是介绍球体的,因为这些图形的绘制原理基本类似。
但是在绘制圆柱体时遇到了一个问题,就是不知道空间中任意一个圆的参数方程。凭大学里学的高等数学知识仅能推导出底面与坐标平面平行的圆的参数方程,如果圆与坐标面成任意夹角就无法解决。使用与坐标面平行的圆绘制出的“类圆柱体”已经可以满足我的程序的需求了,但是绘制出来的毕竟不是一个真正的圆柱。向同学请教了参数方程后后,终于解决了这个问题。
【铺垫:使用WPF 3D绘制三维物体的方法概述】
与Direct 3D类似,在WPF中,任何三维物体都是由三角形组成的。MeshGeometry3D对象定义组成图像的各个三角形顶点和这些顶点的连接方式。该对象的Positions属性是一个Point3D类型的集合,用户记录三角形的各顶点坐标,TriangleIndices属性则描述这些顶点的链接方式。
GeometryModel3D对象的Material和BackMaterial属性可以定义三维物体的表面和背面材质。在本程序中,材质只用到了漫反射材质DiffuseMaterial。Geometry属性指定该三维物体的MeshGeometry3D对象。为此,我们可以为每一个原子、键和平面生成各自的GeometryModel3D对象,这样就可以为每一个元素分别进行着色。
每个GeometryModel3D被承载在一个ModelVisual3D对象中。整个三维场景都被定义在一个Viewport3D对象中。该对象的Children属性是ModelVisual3D的集合。将预先设定的三维物体的ModelVisual3D对象添加到集合中,便可以在Viewport3D视图中显示。
【引子:先了解如何绘制一个球面】
一个球体可以表示成由经线和纬线组成的网格,我们可以将每个网格近似地看成由两个三角形组成的平面,如下图所示。
为了依次生成球面上离散的各点坐标,需要将球面写成参数形式。设球心在坐标原点,球体半径为R,则其参数方程为:
使用参数方程,用双重循环即可生成球面的点。代码如下:
'将球面进行三角形拆分。设球面的参数方程为:
' x = - r * cosφ * sinθ
' y = r * sinφ
' z = - r * cos φ * cosθ
'其中,-π/2≤φ≤π/2,-2π≤θ≤2π
Dim mesh As New MeshGeometry3D
Dim x, y, z, theta, phi As Double
Dim normal As Vector3D '组成球面的某个三角形的法向量
For i As Integer = 0 To Stacks '将球面拆分成Stacks个等距离的薄片(纬度,自上向下)
phi = Math.PI / 2 - i * Math.PI / Stacks '计算该纬度位置的phi角
y = R * Math.Sin(phi) '计算该纬度位置的y轴坐标(假设球心在原点)
For j As Integer = 0 To Slices '将球面纵向切成Slices份(经度方向,自西向东)
theta = j * 2 * Math.PI / Slices '计算该经度位置的theta角
'按照参数方程计算出另外两个坐标值
x = -R * Math.Cos(phi) * Math.Sin(theta)
z = -R * Math.Cos(phi) * Math.Cos(theta)
normal = New Vector3D(x, y, z) '当球心在原点时,某点的法向量就是(x,y,z)
mesh.Positions.Add(normal + center) '某点的坐标:指定的球心+当前计算出的坐标
'计算材质对应的二维坐标,点(j / Slices, i / Stacks)是该点在二维平面展开后对应的坐标
mesh.TextureCoordinates.Add(New Windows.Point(j / Slices, i / Stacks))
Next j
Next i
其中Stacks表示纬度剖分数,Slices为经度拆分数。每计算一个顶点的坐标,便将其添加到Positions集合中。mesh.Normals.Add方法由于指定该点的法向量。该点的法向量方向是球心与该点连线的向量方向,即 ![]() ,而该点的坐标为
,而该点的坐标为![]() ,其中c是球心的坐标。
,其中c是球心的坐标。
接下来需要考虑的问题是如何为球面着色。设想球面按球面轴展开,就成了如下图所示的二维平面。
与顶点集合对应的TextureCoordinates集合指定了填充三维对象表面时顶点与二维图像之间的关系。WPF定义与三维物体表面对应的二维填充平面的左上顶点和右下顶点分别为(0,0)和(1,1),如上图所示的(i,j),其对应的二维向量为 。mesh.TextureCoordinates.Add(i/stacks,j/slices)就是指定该顶点与二维填充平面的对应关系。
顶点和相关集设置好后,需要指定这些顶点如何构成三角形。具体实现方式请参考Lieo3DModel类中GenerateSphereMesh方法。
【进入正题:圆柱体侧面的三角形剖分】
与球体类似,圆柱体按照其轴展开后也是一个矩形。
可以想象,设n表示从底面圆心指向顶面圆心的向量,将一个底面圆上的按照圆的参数方程等间隔地生成,那么顶面相对应的顶点的坐标可按照向量n平移得到。将这样的两个点连起来,连线与轴平行。按照这个思路,只需要生成底面圆上各点的坐标,即可按照图将圆柱剖分成三角形。
空间中任意一个圆的参数方程为:
![]()
其中 ![]() 为圆的法向量。为了计算这两个与法向量相互正交的向量,可以使用向量的叉积运算。
为圆的法向量。为了计算这两个与法向量相互正交的向量,可以使用向量的叉积运算。
设M是空间中任意一个不与圆的法向量共线的向量,令![]() ,这样得到的 就是相互垂直的。将向量归一化后,便得到了参数方程所需要的a,b。
,这样得到的 就是相互垂直的。将向量归一化后,便得到了参数方程所需要的a,b。
参照球面生成的代码,生成圆柱的代码能够很容易写出。具体请下列代码:
''' <summary>
''' 将两底面圆心在 p1、p2 位置,底面半径为 R 的圆柱体进行三角形剖分。
''' </summary>
''' <param name="p1">圆柱上底面圆心的坐标。</param>
''' <param name="p2">圆柱下底面圆心的坐标。</param>
''' <param name="R">圆柱的底面半径。</param>
''' <returns>返回值:代表该圆柱面的MeshGeometry3D对象。</returns>
Public Shared Function GenerateCylinderMesh(ByVal p1 As Point3D, ByVal p2 As Point3D, ByVal R As Double) As MeshGeometry3D
'将圆柱体进行三角形剖分
'空间中圆的参数方程:(x,y,z) = r*(A*cosθ+B*sinθ)+(x0,y0,z0) 【0≤θ≤2π】
' 其中 a、b 是单位向量,且满足 A⊥B⊥n(圆的法向量)
Dim mesh As New MeshGeometry3D
Dim CircleVector As Vector3D = p2 - p1 '从p1点到p2点的3D向量
Dim M As New Vector3D(1, 1, 1)
If Vector3D.AngleBetween(M, CircleVector) < 0.1 Then
M = New Vector3D(1, 0, 0)
End If
Dim A As Vector3D = Vector3D.CrossProduct(CircleVector, M)
Dim B As Vector3D = Vector3D.CrossProduct(CircleVector, A)
A.Normalize()
B.Normalize()
Dim theta As Double
Dim Pos1, Pos2 As Point3D
'设圆与 xz 轴平行
For i As Integer = 0 To Stacks
'计算剖分三角形顶点在参数方程中对应的角度
theta = i / Stacks * Math.PI * 2
Pos1 = R * (A * Math.Cos(theta) + B * Math.Sin(theta)) + p1
Pos2 = R * (A * Math.Cos(theta) + B * Math.Sin(theta)) + p2
mesh.Positions.Add(Pos1)
mesh.Positions.Add(Pos2)
mesh.TextureCoordinates.Add(New Windows.Point(i / Stacks, 0))
mesh.TextureCoordinates.Add(New Windows.Point(i / Stacks, 1))
Next
For i As Integer = 0 To Stacks - 1
mesh.TriangleIndices.Add(i * 2)
mesh.TriangleIndices.Add(i * 2 + 1)
mesh.TriangleIndices.Add(i * 2 + 3)
mesh.TriangleIndices.Add(i * 2)
mesh.TriangleIndices.Add(i * 2 + 3)
mesh.TriangleIndices.Add(i * 2 + 2)
Next
Return mesh
End Function