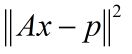线性代数(四十二) : 超定方程组
如果一个线性方程组的方程数大于其未知数的个数,这样的方程组就叫做超定方程组(Overdetermined System).
1 超定方程
对于未知量:
很多时候我们不能直接测得他们的值.却可以测得他们的某些线性组合:
假设可以得到m个这样的线性组合,则可以构造方程组:
其中
为各线性组合的测量值,A为mxn的矩阵,
我们需要检查测量值个数m是否大于我们所关心的未知量的个数,
一旦m>n,此时方程组为超定方程组.通常无解.但是测量值本身就不是精确的.
我们无需要求方程被精确的满足.因此我们只需求出使:
取得最小值的x即可,x的这个值与真实值最为接近.
2 求解超定方程组
定理:
设A是mxn的矩阵,且A只有平凡的零化向量0(否则x不唯一),则使
取得最小值的x恰好是满足下列方程的z:
证明(该证明不是严谨的证明):
首先证明(1)式有唯一解:
(1)式是一个n个未知数n个方程的方程组,该方程组有唯一解当且仅当:
只有平凡解y=0,考虑y的标量积:
因此Ay=0,又因为A只有平凡零化向量,因此y=0.这就说明(1)式有唯一解.
断言:
任取x并将其拆成x=z+y则:
根据假设Az-p与Ay正交由勾股定理:
这就表明当x=z时:
取得最小值.为了求z,将假设条件写为:
利用A的伴随上式可写为:
因为对全体y成立。因此: