算法学习 - 红黑树(Red-Black Trees)
算法学习——深入解析“红黑树”
Learning Algorithms - Red-Black Trees
Stanford Zhang
19 Jun. 2011
本人声明
算法学习系列文章可以说是笔者学习算法过程的笔记,这里面每一个主题都可以在网上找到大量参考资料。但在大量的资料里,很多写的不全,或是解释的不够详细,或是让人看完后,总感觉知其然,不知其所以然。所以笔者在学习的过程中走了很多弯路,这里将算法流程及在我学习过程中遇到的和思考的一些问题,给出详细的解释。
诚然,笔者能力有限,在行文过程中难免有些错误、不妥之处,欢迎批评指正。或是读者有疑问,同样欢迎与我交流。
关于版权,笔者在学习的过程中参考了无数资料,有些已经忘记出处,无法一一列出,甚感抱歉。对于各位作者分享知识的精神,本人敬佩与感激。所以在此,若笔者的文章荣幸能入各位慧眼,可随意转载、引用以及使用。无论注明出处与否,都可。
本文参考
[1] Introduction to Algorithms
赠言
勤:
勤奋是人生第一要义。
勤政是居官首务。
从一个人的勤奋程度, 便可以预知他能成多大的事。
勤奋之道, 精力虽止八分, 却要用到十分, 权势虽有十分, 只可使出五分。
办大事者, 在内贵有志气, 在外贵得人心。
由勤生明。
读万卷书, 行万里路要并行。
家之兴衰, 人之穷通, 皆于勤惰卜之。
天下古今之庸人, 皆以一惰字致败。
天下古今之才人, 皆以一傲字致败。
勤的过头, 也将适得其反。
——曾国藩
*******************************************************************************
注:
在阅读Introduction to Algorithms过程中,发现其伪代码风格有时让人产生误解(至少笔者误解过),故在此笔者将在原代码基础上,用大括号标注程序中的作用域。
*******************************************************************************
i. What?
A red - black tree is a binary search tree with one extra bit of storage per node: its color, which can be either RED or BLACK. By constraining the way nodes can be colored on any path from the root to a leaf, red-black trees ensure that no such path is more than twice as long as any other, so that the tree is approximately balanced.
Each node of the tree now contains the fields color, key, left, right, and p. If a child or the parent of a node does not exist, the corresponding pointer field of the node contains the value NIL. We shall regard these NIL's as being pointers to external nodes (leaves) of the binary search tree and the normal, key-bearing nodes as being internal nodes of the tree.
A binary search tree is a red-black tree if it satisfies the following red-black properties:
1. Every node is either red or black.
2. The root is black.
3. Every leaf (NIL) is black.
4. If a node is red, then both its children are black.
5. For each node, all paths from the node to descendant leaves contain the same number of black nodes.
(以上摘自Introduction to Algorithms。这里要注意不要看潘金贵等翻译的《算法导论》,此书中对红黑树规则5的翻译有误。同时在P168页,关于红黑树插入的示例图中,图3)画的有误,和原书不一样)
ii. How?
红黑树的building过程中,主要有三个操作:Rotations, Insertion, Deletion。其中插入和删除基本的框架和二叉搜索树是一样的,这里不过多解释,这里着重阐述的是旋转,插入和删除这后的调整操作。
*******************************************************************************
Rotations
Figure 1: 二叉查找树中的旋转操作
旋转操作分为左旋和右旋,这两者类似,这里仅介绍左旋。左旋操作代码如下:
void left_rotate(rb_node<T>* x)
{
rb_node<T>* y = x->pRight; // Set y.
x->pRight = y->pLeft; // Turn y's left subtree into x's right subtree.
y->pLeft->pParent = x;
y->pParent = x->pParent; // Link x's parent to y.
if (x->pParent == m_NIL)
{
m_root = y;
}
else
{
if (x == x->pParent->pLeft)
{
x->pParent->pLeft = y;
}
else
{
x->pParent->pRight = y;
}
}
y->pLeft = x; // Put x on y's left.
x->pParent = y;
}
旋转操作的步骤比较清晰,这里不在赘述,但有两个细节要注意:
A. 如图1中所示,注意LEFT-ROTATE(T, x),RIGHT-ROTATE(T, y)和x, y的位置关系;
B. 通常情况下,在做一次左旋转过程中,共有4个结点的属性需要调整,分别为:p[x], x, y, left[y]。
*******************************************************************************
Insertion
红黑树结点的插入,类似二叉搜索树,比较复杂的是在插入之后做的调整操作。
void Insert(T key)
{
rb_node<T>* z = new_node();
z->key = key;
rb_node<T>* y = m_NIL; // find y, y is parent of x/z
rb_node<T>* x = GetRoot();
while (x != m_NIL)
{
y = x;
if (z->key < x->key)
{
x = x->pLeft;
}
else
{
x = x->pRight;
}
}
z->pParent = y;
if (y == m_NIL)
{
m_root = z;
}
else
{
if (z->key < y->key)
{
y->pLeft = z;
}
else
{
y->pRight = z;
}
}
z->pLeft = m_NIL;
z->pRight = m_NIL;
z->color = red;
rb_insert_fixup(z);
}
void rb_insert_fixup(rb_node<T>* z)
{
rb_node<T>* y = 0;
while (z->pParent->color == red)
{
// z's parent is left node
if (z->pParent == z->pParent->pParent->pLeft)
{
// z's uncle y
y = z->pParent->pParent->pRight;
if (y->color == red)
{
z->pParent->color = black; // Case 1 父节点变黑
y->color = black; // Case 1 叔节点变黑
z->pParent->pParent->color = red; // Case 1 祖父节点变红
z = z->pParent->pParent; // Case 1 当前节点移至祖父节点
}
else
{
// z is right node
if (z == z->pParent->pRight)
{
z = z->pParent; // Case 2
left_rotate(z); // Case 2
}
z->pParent->color = black; // Case 3
z->pParent->pParent->color = red; // Case 3
right_rotate(z->pParent->pParent); // Case 3
}
}
else
{
// z's uncle y
y = z->pParent->pParent->pLeft;
if (y->color == red)
{
z->pParent->color = black; // Case 1
y->color = black; // Case 1
z->pParent->pParent->color = red; // Case 1
z = z->pParent->pParent; // Case 1
}
else
{
// z is right node
if (z == z->pParent->pLeft)
{
z = z->pParent; // Case 2
right_rotate(z); // Case 2
}
z->pParent->color = black; // Case 3
z->pParent->pParent->color = red; // Case 3
left_rotate(z->pParent->pParent); // Case 3
}
}
}
m_root->color = black;
}
*******************************************************************************
Deletion
在删除黑色节点之后,需要对红黑树做一些调整,以满足所有规则。
void Delete(T key)
{
rb_node<T>* z = Search(m_root, key);
if (z == m_NIL)
{
return;
}
rb_node<T>* y; // y is the node that will be deleted
rb_node<T>* x; // x is child of y
if (z->pLeft == m_NIL || z->pRight == m_NIL)
{
y = z;
}
else
{
y = Successor(z);
}
// y has only one child node or no node
// so x = y->pLeft / y->pRight / m_NIL
// only one of them
if (y->pLeft != m_NIL)
{
x = y->pLeft;
}
else
{
x = y->pRight;
}
x->pParent = y->pParent;
if (y->pParent == m_NIL)
{
m_root = x;
}
else
{
if (y == y->pParent->pLeft)
{
y->pParent->pLeft = x;
}
else
{
y->pParent->pRight = x;
}
}
if (y != z)
{
z->key = y->key;
}
if (y->color == black)
{
rb_delete_fixup(x);
}
delete_node(y);
}
void rb_delete_fixup(rb_node<T>* x)
{
rb_node<T>* w = 0; // x's siblin w
while (x != m_root && x->color == black)
{
if (x == x->pParent->pLeft)
{
w = x->pParent->pRight;
if (w->color == red)
{
w->color = black; // Case 1
w->pParent->color = red; // Case 1
left_rotate(x->pParent); // Case 1
w = x->pParent->pRight; // Case 1
}
if (w->pLeft->color == black && w->pRight->color == black)
{
w->color = red; // Case 2
x = x->pParent; // Case 2
}
else
{
if (w->pRight->color == black)
{
w->pLeft->color = black; // Case 3
w->color = red; // Case 3
right_rotate(w); // Case 3
w = x->pParent->pRight; // Case 3
}
w->color = x->pParent->color; // Case 4
x->pParent->color = black; // Case 4
w->pRight->color = black; // Case 4
left_rotate(x->pParent); // Case 4
x = m_root;
}
}
else
{
w = x->pParent->pLeft;
if (w->color == red)
{
w->color = black; // Case 1
w->pParent->color = red; // Case 1
right_rotate(x->pParent); // Case 1
w = x->pParent->pLeft; // Case 1
}
if (w->pLeft->color == black && w->pRight->color == black)
{
w->color = red; // Case 2
x = x->pParent; // Case 2
}
else
{
if (w->pLeft->color == black)
{
w->pRight->color = black; // Case 3
w->color = red; // Case 3
left_rotate(w); // Case 3
w = x->pParent->pLeft; // Case 3
}
w->color = x->pParent->color; // Case 4
x->pParent->color = black; // Case 4
w->pLeft->color = black; // Case 4
right_rotate(x->pParent); // Case 4
x = m_root;
}
}
}
x->color = black;
}
*******************************************************************************
iii. Why?
*******************************************************************************
Insertion
*******************************************************************************
约定:
1. 当前插入的节点标记为z;
2. z的叔叔节点标记为y;
3. z的父节点标记为p[z],其他节点类似;
4. z节点的颜色标记为color[z],其他节点类似;
5. p[z]的左右子节点分别标记为left[p[z]], right[p[z]],其他节点类似。
插入后需要进行调整的Case:
Case 1: z的叔叔y是红色
Case 2: z的叔叔y是黑色的,而且z是右孩子
Case 3: z的叔叔y是黑色的,而且z是左孩子
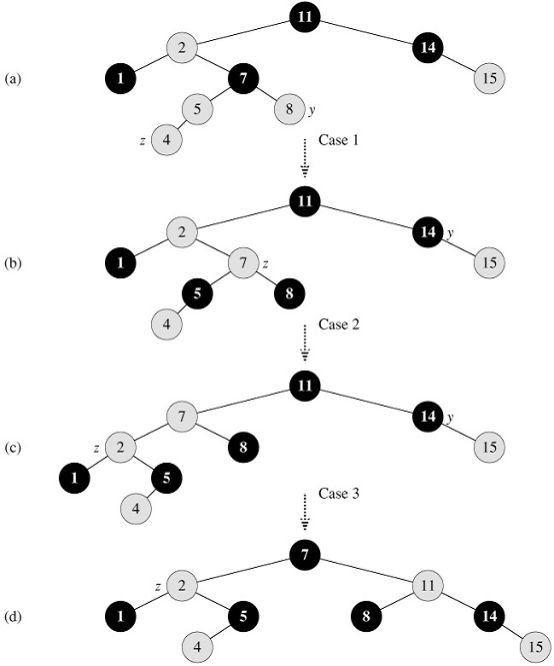
Figure 2: The operation of rb_insert_fixup
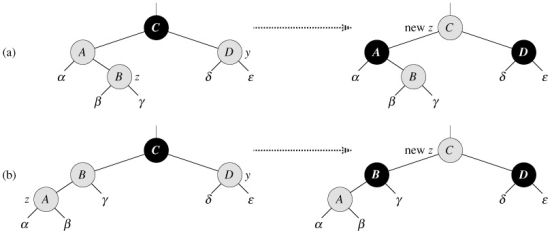
Figure 3: Case 1 of the procedure rb_insert
Figure 4: Cases 2 and 3 of the procedure rb_insert
阐述:
1. 根据规则5插入的节点标记为红色,但这可能违反红黑树规则,需要进行调整,调用RB_INSERT_FIXUP方法进行调整;
2. 在RB_INSERT_FIXUP过程中,while循环的条件为color[p[z]] == RED。因为插入节点的颜色为红,而其父节点也为RED,这违反了规则4,所以才调整,这是唯一条件。如果color[p[z]] == BLACK,插入的新节点没有违反任何规则,不用调整;
3. Case 1比较容易解决,由父、叔节点为红色,可判断祖父节点必为黑色,根据规则4。将父、叔节点调整为黑色,祖父节点调整为红色,这样就可以让以p[p[z]]为根的子树满足红黑树的规则。此时,当前节点调整为p[p[z]],因为p[p[z]]的颜色进行过调整,有可能会使p[p[z]]与其父节点违反规则,所以需要继续进行循环调整。
4. Case 2无法直接解决,须转换成Case 3,才能解决。首先将当前节点调整为p[z],然后做一次旋转,Case 2就转换Case 3。可以理解为z和p[z]角色互换,为的就是转换成Case 3。
5. Case 3当前节点的祖父节点设置为红色,父节点设置为黑色,以祖父节点为当前节点,做一次旋转,此时各规则都已满足。当前节点为红色,父节点也为红色,祖父节点原来是满足规则的,所以必为黑色,叔叔节点也为黑色,现在将祖父节点和父节点的颜色互换,就可以保证从当前节点、父节点、祖父节点到叔叔节点这个序列中没有连续的红色节点,此时以祖父节点为当前节点,做一次旋转,以保持规则5。此时当前调整的子树是以p[z]为根的子树,而p[z]为黑色,所以不用再继续循环调整。
6. 当打循环结束,不要忘记将整个树的根节点设置为黑色。
*******************************************************************************
Deletion
*******************************************************************************
约定:
1. 当前插入的节点标记为x;
2. x的兄弟节点标记为w;
3. x的父节点标记为p[x],其他节点类似;
4. x节点的颜色标记为color[x],其他节点类似;
5. p[x]的左右子节点分别标记为left[p[x]], right[p[x]],其他节点类似。
插入后需要进行调整的Case:
Case 1: x兄弟w是红色的
Case 2: x的兄弟w是黑色的,而且w的两个孩子都是黑色的
Case 3: x的兄弟w是黑色的,w的左孩子是红色的,右孩子是黑色的
Case 4: x的兄弟w是黑色的,w的右孩子是红色的
Figure 5: The cases in the while loop of the procedure rb_delete_fixup
阐述:
1. 当做删除操作时,要注意两种情况:一、如果删除的节点没有子节点或只有一个子节点,则将删除节点的子节点作为删除节点父节点的子节点,并删除要删除的节点及按规则调整;二、如果要删除的节点有两个子节点,则找出当前节点的后继节点,并将后继节点的值赋给当前节点,同时删除后继节点(操作同前一种情况)。
2. 只有在删除了黑节点的情况下才需要调整,因为这破坏了黑高度;
3. 情况1不能直接解决,须转换成情况2,3,4;
4. 情况3不能直接解决,须转换成情况4;
5. 从程序可看出,虽然有四种情况,但跳出循环的出口有两个,就是情况2和情况4,而情况2则是当x父节点为红色时,跳出循环,此时当前节点为x的父节点。如果是情况2跳出循环,则是将x的父节点涂黑,x的兄弟节点涂红,这样x的子树黑高度在删除之后少了一个,现在又加了回来,而且p[x]的右子树黑高度也不变。其他情况最后都转换成情况四,情况1,2,3没有直接的解决方案。而情况4跳出循环则是将p[x]的右子树中的一个结点涂黑放入左子树中,使子树平衡。而同时右子树黑高度不变,从右子树中拿一个放入到左子树,那右子树必定有一个节点是从红色变为黑色,这样从而右子树不变,而左子树也多了一个黑节点;
6. 情况1下x兄弟w是红色,则做一下转换,转换成x兄弟w是黑色的情况;
7. 当x的父节点为红色时,就直接跳出循环,再将其涂黑,否则继续循环。这种情况将x兄弟节点的黑色上移一层,使父节点为黑色,这样同时也增加了x子树的黑高度弥补了删除黑节点减少的黑高度;
8. 情况3须将其转换为情况4,不然无法直接解决,仅调整为情况4,黑高度未变;
9. 情况4从兄弟节点w中拿一个节点,放入x的子树中并涂为黑色,弥补删除的节点减去黑高度。
iv. Source Code
以下是完整的红黑树实现的源代码:
#ifndef _RB_TREE_H_
#define _RB_TREE_H_
enum rb_tree_color{red, black};
template<class T>
struct rb_node
{
T key;
rb_node<T>* pParent;
rb_node<T>* pLeft;
rb_node<T>* pRight;
rb_tree_color color;
};
template<class T>
class CRebBlackTree
{
// private data member
private:
rb_node<T>* m_root; // only one
rb_node<T>* m_NIL; // only one
// private function member
private:
rb_node<T>* new_node(void)
{
rb_node<T>* n = new rb_node<T>();
n->color = red;
n->pParent = 0;
n->pLeft = 0;
n->pRight = 0;
return n;
}
void delete_node(rb_node<T>* n)
{
delete n;
n = 0;
}
//empty the tree
void Clear(rb_node<T>* root)
{
if (root == m_NIL)
{
return;
}
else
{
Clear(root->pLeft);
Clear(root->pRight);
if (root == root->pParent->pLeft)
{
root->pParent->pLeft = m_NIL;
}
else
{
root->pParent->pRight = m_NIL;
}
PrintNode(root);
printf("\n");
delete_node(root);
}
}
rb_node<T>* Minimum(rb_node<T>* node)
{
rb_node<T>* ret = node;
while (ret->pLeft != m_NIL)
{
ret = ret->pLeft;
}
return ret;
}
rb_node<T>* Maximum(rb_node<T>* node)
{
rb_node<T>* ret = node;
while (ret->pRight != m_NIL)
{
ret = ret->pRight;
}
return ret;
}
rb_node<T>* Successor(rb_node<T>* x)
{
if (x->pRight != m_NIL)
{
return Minimum(x->pRight);
}
rb_node<T>* y = x->pParent;
//node is right node
while (y != m_NIL && x == y->pRight)
{
x = y;
y = y->pParent;
}
return y;
}
void left_rotate(rb_node<T>* x)
{
rb_node<T>* y = x->pRight; // Set y.
x->pRight = y->pLeft; // Turn y's left subtree into x's right subtree.
y->pLeft->pParent = x;
y->pParent = x->pParent; // Link x's parent to y.
if (x->pParent == m_NIL)
{
m_root = y;
}
else
{
if (x == x->pParent->pLeft)
{
x->pParent->pLeft = y;
}
else
{
x->pParent->pRight = y;
}
}
y->pLeft = x; // Put x on y's left.
x->pParent = y;
}
void right_rotate(rb_node<T>* y)
{
rb_node<T>* x = y->pLeft;
y->pLeft = x->pRight;
x->pRight->pParent = y;
x->pParent = y->pParent;
if (y->pParent == m_NIL)
{
m_root = x;
}
else
{
if (y == y->pParent->pLeft)
{
y->pParent->pLeft = x;
}
else
{
y->pParent->pRight = x;
}
}
x->pRight = y;
y->pParent = x;
}
void rb_insert_fixup(rb_node<T>* z)
{
rb_node<T>* y = 0;
while (z->pParent->color == red)
{
// z's parent is left node
if (z->pParent == z->pParent->pParent->pLeft)
{
// z's uncle y
y = z->pParent->pParent->pRight;
if (y->color == red)
{
z->pParent->color = black; // Case 1 父节点变黑
y->color = black; // Case 1 叔节点变黑
z->pParent->pParent->color = red; // Case 1 祖父节点变红
z = z->pParent->pParent; // Case 1 当前节点移至祖父节点
}
else
{
// z is right node
if (z == z->pParent->pRight)
{
z = z->pParent; // Case 2
left_rotate(z); // Case 2
}
z->pParent->color = black; // Case 3
z->pParent->pParent->color = red; // Case 3
right_rotate(z->pParent->pParent); // Case 3
}
}
else
{
// z's uncle y
y = z->pParent->pParent->pLeft;
if (y->color == red)
{
z->pParent->color = black; // Case 1
y->color = black; // Case 1
z->pParent->pParent->color = red; // Case 1
z = z->pParent->pParent; // Case 1
}
else
{
// z is right node
if (z == z->pParent->pLeft)
{
z = z->pParent; // Case 2
right_rotate(z); // Case 2
}
z->pParent->color = black; // Case 3
z->pParent->pParent->color = red; // Case 3
left_rotate(z->pParent->pParent); // Case 3
}
}
}
m_root->color = black;
}
void rb_delete_fixup(rb_node<T>* x)
{
rb_node<T>* w = 0; // x's siblin w
while (x != m_root && x->color == black)
{
if (x == x->pParent->pLeft)
{
w = x->pParent->pRight;
if (w->color == red)
{
w->color = black; // Case 1
w->pParent->color = red; // Case 1
left_rotate(x->pParent); // Case 1
w = x->pParent->pRight; // Case 1
}
if (w->pLeft->color == black && w->pRight->color == black)
{
w->color = red; // Case 2
x = x->pParent; // Case 2
}
else
{
if (w->pRight->color == black)
{
w->pLeft->color = black; // Case 3
w->color = red; // Case 3
right_rotate(w); // Case 3
w = x->pParent->pRight; // Case 3
}
w->color = x->pParent->color; // Case 4
x->pParent->color = black; // Case 4
w->pRight->color = black; // Case 4
left_rotate(x->pParent); // Case 4
x = m_root;
}
}
else
{
w = x->pParent->pLeft;
if (w->color == red)
{
w->color = black; // Case 1
w->pParent->color = red; // Case 1
right_rotate(x->pParent); // Case 1
w = x->pParent->pLeft; // Case 1
}
if (w->pLeft->color == black && w->pRight->color == black)
{
w->color = red; // Case 2
x = x->pParent; // Case 2
}
else
{
if (w->pLeft->color == black)
{
w->pRight->color = black; // Case 3
w->color = red; // Case 3
left_rotate(w); // Case 3
w = x->pParent->pLeft; // Case 3
}
w->color = x->pParent->color; // Case 4
x->pParent->color = black; // Case 4
w->pLeft->color = black; // Case 4
right_rotate(x->pParent); // Case 4
x = m_root;
}
}
}
x->color = black;
}
public:
CRebBlackTree(void)
{
m_NIL = new_node();
m_NIL->pParent = m_NIL;
m_NIL->pLeft = m_NIL;
m_NIL->pRight = m_NIL;
m_root = m_NIL;
m_root->color = black;
}
//release memory (all nodes)
~CRebBlackTree()
{
printf("clear tree...\n");
Clear(m_root);
delete_node(m_NIL);
}
rb_node<T>* GetRoot(void)
{
return m_root;
}
void PrintNode(rb_node<T>* n)
{
if (n != m_NIL)
{
printf("%d ", n->key);
PrintNode(n->pLeft);
PrintNode(n->pRight);
}
}
rb_node<T>* Search(rb_node<T>* x, T key)
{
if (x == m_NIL || key == x->key)
{
return x;
}
if (key < x->key)
{
return Search(x->pLeft, key);
}
else
{
return Search(x->pRight, key);
}
}
void Insert(T key)
{
rb_node<T>* z = new_node();
z->key = key;
rb_node<T>* y = m_NIL; // find y, y is parent of x/z
rb_node<T>* x = GetRoot();
while (x != m_NIL)
{
y = x;
if (z->key < x->key)
{
x = x->pLeft;
}
else
{
x = x->pRight;
}
}
z->pParent = y;
if (y == m_NIL)
{
m_root = z;
}
else
{
if (z->key < y->key)
{
y->pLeft = z;
}
else
{
y->pRight = z;
}
}
z->pLeft = m_NIL;
z->pRight = m_NIL;
z->color = red;
rb_insert_fixup(z);
}
void Delete(T key)
{
rb_node<T>* z = Search(m_root, key);
if (z == m_NIL)
{
return;
}
rb_node<T>* y; // y is the node that will be deleted
rb_node<T>* x; // x is child of y
if (z->pLeft == m_NIL || z->pRight == m_NIL)
{
y = z;
}
else
{
y = Successor(z);
}
// y has only one child node or no node
// so x = y->pLeft / y->pRight / m_NIL
// only one of them
if (y->pLeft != m_NIL)
{
x = y->pLeft;
}
else
{
x = y->pRight;
}
x->pParent = y->pParent;
if (y->pParent == m_NIL)
{
m_root = x;
}
else
{
if (y == y->pParent->pLeft)
{
y->pParent->pLeft = x;
}
else
{
y->pParent->pRight = x;
}
}
if (y != z)
{
z->key = y->key;
}
if (y->color == black)
{
rb_delete_fixup(x);
}
delete_node(y);
}
};
#endif