利用余弦定理制作连杆效果

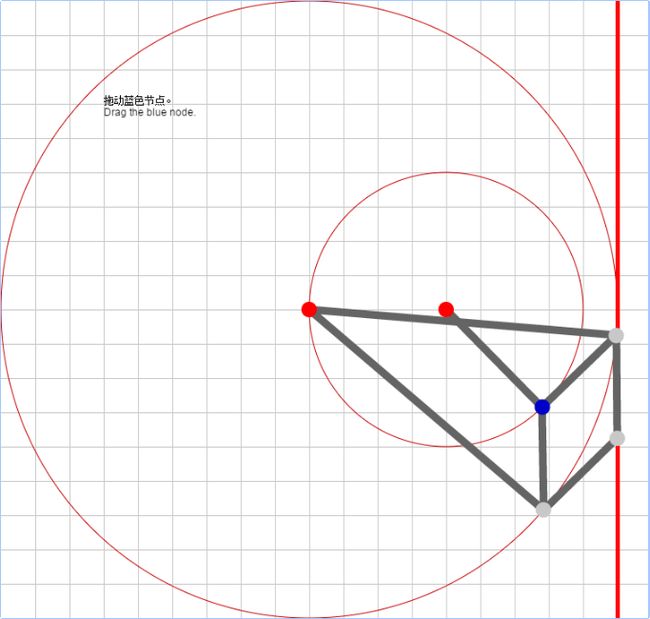
前些天看看MIT的公开课：折叠几何算法，里面演示了一段小程序，通过几根杆子的连接，可以将圆周运动转换为直线运动。效果是这样的：

问题源于蒸汽机的发明：如何将上下方向的活塞运动转化为推动轮子滚动的圆周运动呢？

公开课中有一个Javascript的展示，我对这个程序产生了强烈的兴趣。于是用Processing实现了一下。大体思路如下：

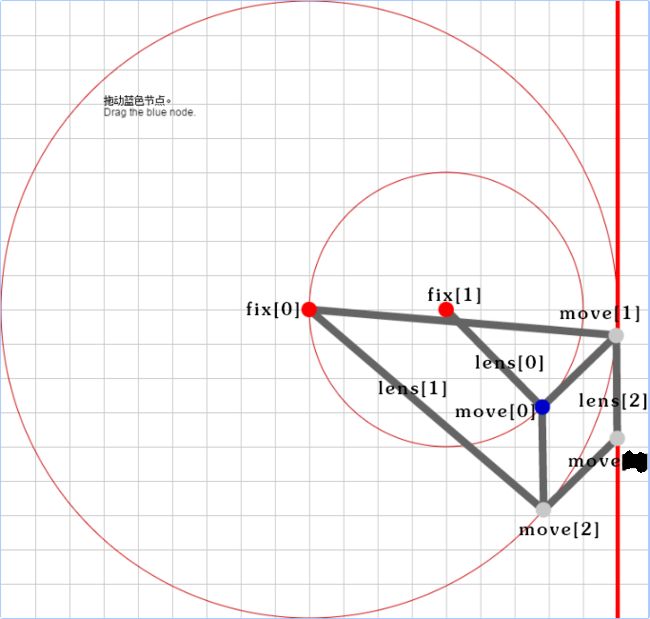
图中有3个长度，2个固定点，4个移动点，分别建立数组，如下图：

其中，以一个格子的长度(bs)为单位，长度分别为：lens[0] = 4, lens[1] = 9, lens[2] = 3

拖动move[0]，确定move[0]的坐标，使用余弦定理确定move[1]和move[2]的坐标，再通过余弦定理确定move[3]的坐标。

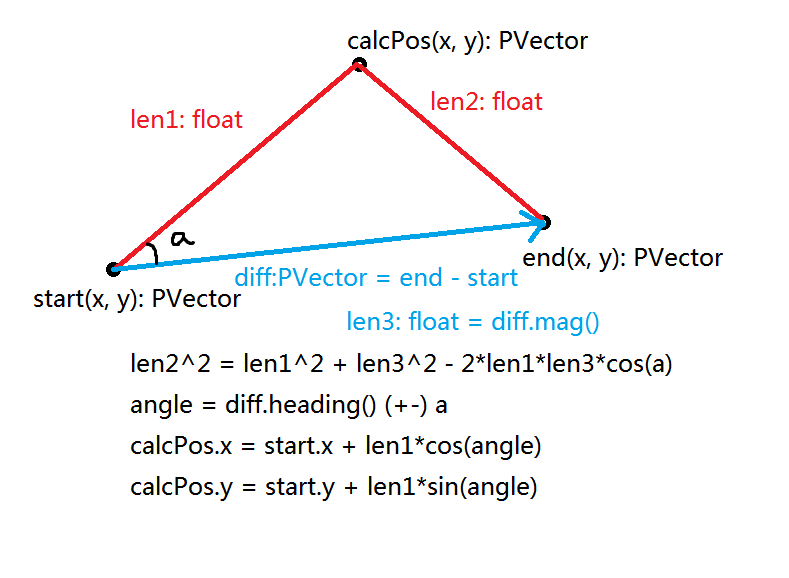
利用余弦定理计算的函数是calcPos函数，要求输入起始向量和终止向量，以及两个长度以确定第3个点的坐标。思路及图解如下：

程序如下：

int bs = 40;
float[] lens;
PVector[] fix;
PVector[] move;
boolean canReach;
int pSize = 20;
boolean isDrag = false;

void setup() {
  size(840, 720);
  background(255);
  lens = new float[3];
  fix = new PVector[2];
  move = new PVector[4];
  canReach = true;
  fix[0] = new PVector(9*bs, 9*bs);
  fix[1] = new PVector(13*bs, 9*bs);
  lens[0] = 4*bs;
  lens[1] = 9*bs;
  lens[2] = 3*bs;
  move[0] = new PVector(17*bs, 9*bs);

  move[1] = calcPos(fix[0], move[0], lens[1], lens[2], -1);
  move[2] = calcPos(fix[0], move[0], lens[1], lens[2], 1);
  move[3] = calcPos(move[1], move[2], lens[2], lens[2], -1);
  
}

void draw() {
  background(255);
  drawGrid();
  fill(0);
  text("拖动蓝色节点。\nDrag the blue node.", 3*bs, 3*bs);
  stroke(255, 0, 0);
  strokeWeight(5);
  line(18*bs, 0, 18*bs, height);
  
  canReach = true;
  
  if (isDrag) {
    float angle = atan2(mouseY - fix[1].y, mouseX - fix[1].x);
    PVector move0 = new PVector(fix[1].x + cos(angle)*lens[0], fix[1].y + sin(angle)*lens[0]);
    PVector move1 = calcPos(fix[0], move0, lens[1], lens[2], -1);
    PVector move2 = calcPos(fix[0], move0, lens[1], lens[2], 1);
    PVector move3 = calcPos(move1, move2, lens[2], lens[2], -1);
    
    if (canReach) {
      move[0] = move0.get();
      move[1] = move1.get();
      move[2] = move2.get();
      move[3] = move3.get();
    }
  }
  
  update();
}

PVector calcPos(PVector start, PVector end, float len1, float len2, int sign) {
  PVector diff = PVector.sub(end, start);
  float len3 = diff.mag();
  float value = (len1*len1 + len3*len3 - len2*len2)/(2*len1*len3);
  if (abs(value) > 1) {
    canReach = false;
    return new PVector(0, 0);
  }
  float angle = diff.heading();
  angle += sign * acos(value);
  PVector pos = new PVector(len1 * cos(angle), len1*sin(angle));
  return PVector.add(start, pos);
}

void drawGrid() {
  stroke(200);
  strokeWeight(1);
  int i;
  for (i = 1; i < width / bs; i++)
    line(i*bs, 0, i*bs, height);
  for (i = 1; i < height / bs; i++)
    line(0, i*bs, width, i*bs);
  noFill();
  stroke(200, 0, 0);
  ellipse(9*bs, 9*bs, 18*bs, 18*bs);
  ellipse(13*bs, 9*bs, 8*bs, 8*bs);
}

void update() {
  stroke(100);
  strokeWeight(pSize * 0.5);
  line(fix[1].x, fix[1].y, move[0].x, move[0].y);
  line(fix[0].x, fix[0].y, move[1].x, move[1].y);
  line(move[1].x, move[1].y, move[0].x, move[0].y);
  line(fix[0].x, fix[0].y, move[2].x, move[2].y);
  line(move[0].x, move[0].y, move[2].x, move[2].y);
  line(move[1].x, move[1].y, move[3].x, move[3].y);
  line(move[2].x, move[2].y, move[3].x, move[3].y);
  
  noStroke();
  if (isDrag || dist(mouseX, mouseY, move[0].x, move[0].y) < pSize/2) {
    if (mousePressed) {
      if (!isDrag)
        isDrag = true;
      fill(0);
    } else
      fill(120);
  } else
    fill(0, 0, 200);
  ellipse(move[0].x, move[0].y, pSize, pSize);
  fill(255, 0, 0);
  ellipse(fix[0].x, fix[0].y, pSize, pSize);
  ellipse(fix[1].x, fix[0].y, pSize, pSize);
  
  fill(200);
  ellipse(move[1].x, move[1].y, pSize, pSize);
  ellipse(move[2].x, move[2].y, pSize, pSize);
  ellipse(move[3].x, move[3].y, pSize, pSize);
}

void mouseReleased() {
  isDrag = false;
}