【数据挖掘】最优化算法入门

简介

    optimization用来解决以下问题：有多个变量协作，多种可能方法，输出很大程度上依赖各种变量的协作。

    预测：通过尝试多种不同方法，并为它们打分来决定其效果。

#!/usr/bin/python
import time
import random
import math

#元组中存放的是人和其家乡
people = [('Seymour','BOS'),('Franny','DAL'),('Zooey','CAK'),('Walt','MIA'),
         ('Buddy','ORD'),('Les','OMA')]
destination='LGA'

flights={}
#将小时格式时间转换为分钟
def getminutes(t):
  x=time.strptime(t,'%H:%M')
  return x[3]*60+x[4]
#schedule.txt的文件格式：DAL,LGA,10:30,14:57,290
#其中DAL为起飞地、LGA为目的地，以及起飞时间、到达时间和价格
def loadflights(flightInfo):
    fp = open(flightInfo,'r')
    for line in fp.readlines():
        origin,dest,depart,arrive,price=line.strip().split(',')
        flights.setdefault((origin,dest),[])
        flights[(origin,dest)].append((depart,arrive,price))
#r:[1,4,3,2,7,3,6,3,2,4,5,3]，6个人乘坐的航班信息
#此列表代表了一个解决方案
#因为涉及到来回，所以r的长度为人数*2，所以第一和第二个元素代表了某人的去回的两趟
#航班信息
def printschedual(r):
    for d in range(len(r)/2):
      name=people[d][0]
      origin=people[d][1]
      out=flights[(origin,destination)][r[d]]
      ret=flights[(destination,origin)][r[d+1]
      print '%10s%10s %5s-%5s $%3s %5s-%5s $%3s' % (name,origin,\
                                                    out[0],out[1],out[2],\
                                                    ret[0],ret[1],ret[2])  

代价函数

    代价函数是使用最优化解决任何问题的关键。任何最优化的目标：找到一个输入集合（此例中就是航班信息），最小化代价函数。代价函数会考虑多个因素的影响，比如此例中会考虑到机票价格、等待时间、旅行时间、租车等。

#计算解决方案r的总成本，此例只考虑航班机票价格和等待时间两个因素  
#每个人必须在目的地机场等待直到最晚到达的人到达，同时返回时他们同时达到机场，等候他们的航班
def schedulecost(r):
    tprice=0#航班总价格之和
    latestarrive=0#最晚到达
    earliestdep=24*60#最早离开
    for i in range(len(r)/2):
        origin=people[i][0]
        #去航班
        outbound=flights[(origin,destination)][int(r[i])]
        #回航班
        returnf=flights[(destination,origin)][int(r[i+1])]  
        #航班票价
        tprice+=outbound[2]
        tprice+=returnf[2]
        #记录最晚到达、最早离开时间
        if latestarrive < getminutes(outbound[1]): latestarrive=getminutes(outbound[1])
        if earliestdep > getminutes(returnf[0]):earliestdep=getminutes(returnf[0])
    twaittime=0
    for i in range(len(r)/2):
        origin=people[i][0]
        outbound=flights[(origin,destination)][int(r[i])]
        returnf=flights[(destination,origin)][int(r[i+1])]  
        twaittime += latestarrive - getminutes(outbound[1])
        twaittime += getminutes(returnf[0]) - earliestdep 
    return twaittime + tprice

随机搜索

#随机搜索并不是一个好的优化方法，但是它易于理解算法的思想
#domain是一个2元tuple的列表，tuple指定了变量的最大值和最小值
def randomoptimize(domain,costfunc):
    best=999999999
    bestr=None
    for i in range(1000):#遍历1000次
        #随机生成一个解决方案
        r = [random.randint(domain[j][0],domain[j][1]) for j in range(len(domain))]  
        cost = costfunc(r)
        #找到最小的代价
        if cost < best:
            best=cost
            bestr=r
    return bestr

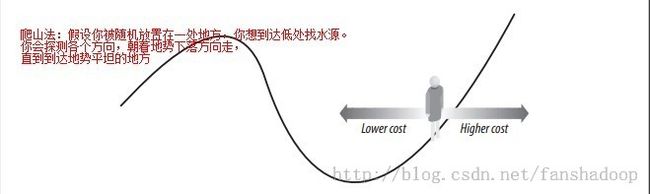
爬山法(Hill climbing)

    随机搜索并不是有效的方法，它没有利用已经找到的好的解决方案，因为随机搜索在周围跳转，不能自动查找类似的解决方案。

def hillclimb(domain,costfunc):
    #初始化，随机生成一个解决方案
    sol = [random.randint(domain[j][0],domain[j][1]) for j in range(len(domain))]
    while True:
        neighbors=[]#创建sol的所有邻居，通过修改sol[j]的值
        for j in range(len(domain)):
            if sol[j] > domain[j][0]:#大于最小
                neighbors.append(sol[0:j]+[sol[j]+1]+sol[j+1:])#将sol[j]元素加1
            if sol[j]<domain[j][1]:#小于最大
                neighbors.append(sol[0:j]+[sol[j]-1]+sol[j+1:])#将sol[j]元素减1
        best=current=costf(sol)#当前sol的代价
        for i in range(len(neighbors)):
            cost=costf(neighbors[j])
            if cost < best:
                best=cost
                sol=neighbors[j]
        #若没有提高，则返回        
        if best == current:
            break
    return sol

模拟退火法

算法思想：

    1）开始以随机一个解决方案，使用一个变量代表温度，此变量开始很高，逐渐变低
    2）在每次迭代，解决方案中的一个数字被随机选择，且朝一个方向改变。
    3）如果新的代价低，则新的解决方案成为当前的解决方案，这点很像爬山法。然而，如果代价更高的话，新的解决方案以一定可能性任然是当前的解决方案，主要是尝试避免本地最小问题。

def annealingoptimize(domain,costf,t=10000.0,cool=0.95,step=1):
    #初始化解决方案
    vec = [float(random.randint(domain[i][0],domain[i][1])) for i in range(len(domain))]
    while t > 0.1:
        #随机选择一个
        i=random.randint(0,len(domain)-1)
        #随机选择一个方向变换
        direction=random.randint(-step,step)
        #复制集合
        vecb=vec[:]
        vecb[i]+=direction
        #若变更后的vecb[i]小于最小值domain[i][0]，vecb[i]变更为最小值
        #若变更后的vecb[i]大于最大值domain[i][1]，vecb[i]变更为最大值
        if vecb[i]<domain[i][0]: vecb[i]=domain[i][0]
        elif vecb[i]>domain[i][1]: vecb[i]=domain[i][1]   
        #计算变更前后的代价
        ea=costf(vec)
        eb=costf(vecb)     
        p=pow(math.e,(-eb-ea)/t)
        #变更后的代价小于变更前的代价或随机数小于某概率p，变更解决方案
        if (eb<ea or random.random()<p):
           vec=vecb
        #降温   
        t=t*cool
    return vec

基因算法

#基因算法  
def geneticoptimize(domain,costf,popsize=50,step=1,
                    mutprod=0.2,elite=0.2,maxiter=100):
    #变异操作,随机选择vec中的一个元素进行处理，增大或减小，最后返回编译后的vec
    def mutate(vec):
        i=random.randint(0,len(domain)-1)
        if random.random()<0.5 and vec[i]>domain[i][0]:
            return vec[0:i]+[vec[i]-step]+vec[i+1:]
        elif vec[i]<domain[i][1]:
            return vec[0:i]+[vec[i]+step]+vec[i+1:]    
    #结合操作，将r1和r2在随机位置前后结合成新的解决方案      
    def crossover(r1,r2):
        i=random.randint(1,len(domain)-2)
        return r1[0:i]+r2[i:]    
    #构建初始化物种，pop物种大小
    pop=[]
    for i in range(popsize):
        vec=[random.randint(domain[i][0],domain[i][1]) for i in range(len(domain))]
        pop.append(vec)
    #最终优胜者的个数    
    topelite=int(elite*popsize)
    #主循环
    for i in range(maxiter):
        scores=[(costf(v),v) for v in pop]#为初始物种计算代价
        scores.sort()
        ranked=[v for (s,v) in scores]#排序后的解决方案
        pop=ranked[0:topelite]#选取前topelite个解决方案
        while len(pop)<popsize:#添加变异或组合后的解决方案，最终保持优胜者个数不变
            if random.random()<mutprob:
                # Mutation
                c=random.randint(0,topelite)
                pop.append(mutate(ranked[c])) 
            else:
                # Crossover
                c1=random.randint(0,topelite)
                c2=random.randint(0,topelite)
                pop.append(crossover(ranked[c1],ranked[c2]))
    return scores[0][1]